I. Критерии однородности выборок

Проверка статистических гипотез.

(описание работы соответствует функциям Excel, в R-project используйте аналогичные функции)

I. Критерии однородности выборок

1.Смоделируйте две выборки 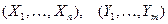из нормального распределения с произвольными математическими ожиданиями 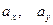и произвольными дисперсиями 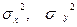. (Положите, например, n=50, m=30)

2.Проверьте гипотезу однородности 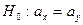, считая дисперсии известными. Примените для проверки двух выборочный 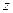- тест, вычислите статистику

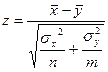
Найдите 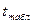соответствующее вероятности ошибки первого рода 0,05, с помощью таблицы стандартного нормального распределения или с помощью функции Excel НОРМСТОБР (можно также воспользоваться функцией НОРМОБР, указав в качестве среднего значения 0, а в качестве стандартного отклонения 1). Для того чтобы правильно воспользоваться функцией НОРМСТОБР, необходимо учесть, что значение поля Вероятность в этой функции представляет собой вероятность 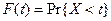, т.е. равно площади под графиком плотности от 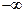до 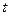, следует взять значение вероятности равное 0,95+0,05/2=0,975. Это значение указывается в поле Вероятность.

3.Сравните значение вычисленной статистики с найденным значением. По результатам сравнения примите или отвергните проверяемую гипотезу.

4.Проверьте полученные результаты с помощью пакета Анализ данных в Excel.

5. Для смоделированных выборок проверьте гипотезу о равенстве дисперсий 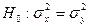c помощью двухвыборочного F- теста для дисперсий. Вычислите статистику:

,

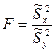Найдите 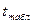соответствующее вероятности ошибки первого рода 0,05, с помощью таблиц распределения Фишера с числами степеней свободы n-1 и m-1 или с помощью функции Fраспобр в Excel.

6. Сравните вычисленное значение статистики с найденным табличным значением и сделайте вывод о принятии или непринятии гипотезы равенства дисперсий.

7. Проверьте полученные результаты с помощью пакета Анализ данных в Excel.

8. Смоделируйте две выборки 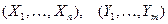из нормального распределения с произвольными математическими ожиданиями 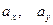и равными дисперсиями 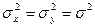. (Положите, например, n=50, m=30).

9. Проверьте гипотезу однородности 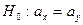, с помощью двухвыборочного t-теста, считая дисперсии неизвестными, но одинаковыми. На практике этот тест применяют для проверки гипотезы о равенстве средних, если применение двухвыборочного F-теста к изучаемым выборкам показало, что можно принять гипотезу о равенстве дисперсий. Вычислите статистику:

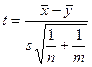, где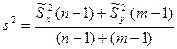

Найдите 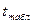соответствующее вероятности ошибки первого рода 0,05, с помощью таблиц распределения Стьюдента с числом степеней свободы n+m-2 или с помощью функции Стьюдраспобр в Excel.

10. Сравните вычисленное значение статистики с найденным табличным значением и сделайте вывод о принятии или непринятии гипотезы равенства средних.

11. Проверьте полученные результаты с помощью пакета Анализ данных в Excel.

12. Смоделируйте две выборки 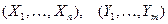из нормального распределения с произвольными математическими ожиданиями 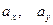и равными дисперсиями 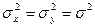. (Положите, например, n=9, m=7).

13. Примените критерий Уилкоксона к проверке гипотезы о статистической однородности двух выборок (двусторонняя альтернатива, 5% уровень значимости).

14. Оформите отчет по всем выполненным заданиям. (Отчет оформляется в MS Word 2003 или в подобном редакторе)