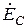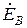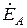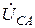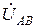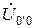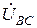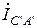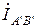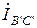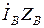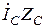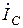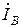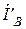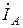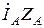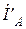Решение

Приемник звезда

Фаза А 0' R = 15 Ом; X_L = 2 Ом; X_С = 10 Ом.

Фаза В 0' R = 15 Ом; X_L = 2 Ом; X_С = 10 Ом.

Фаза С 0' R = 10 Ом; X_L = 20 Ом; X_С = 8 Ом.

Приемник треугольник

Фаза А ' В ' R = 6 Ом; X_L = 16 Ом; X_С = 8 Ом.

Фаза В ' С ' R = 8 Ом; X_L = 26 Ом; X_С = 32 Ом.

Фаза С ' А ' R = 4 Ом; X_L = 15 Ом; X_С = 12 Ом.

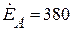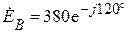В; 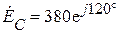В; В.

Для заданной схемы рис.1 найти все токи ветвей, проверить баланс мощностей, построить векторную диаграмму напряжений и токов.

	Рис. 1

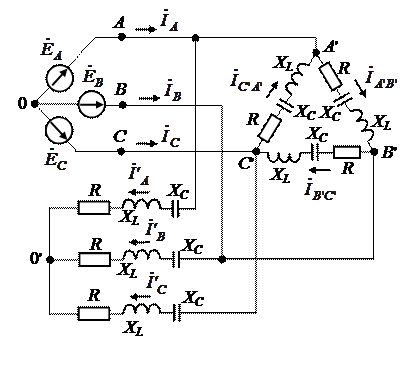Решение

Вычислим общие сопротивления фаз треугольника.

;

;

.

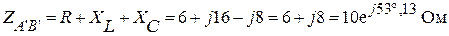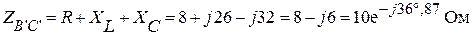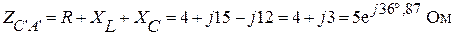Преобразуем звезду сопротивлений в эквивалентный треугольник. Для этой цели, предварительно, вычислим общие сопротивления фаз звезды.

;

;

.

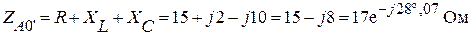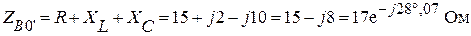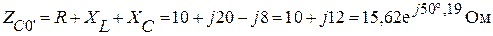Используя формулы приведения, вычислим фазные сопротивления эквивалентного треугольника:

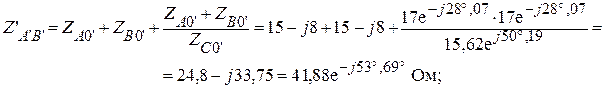
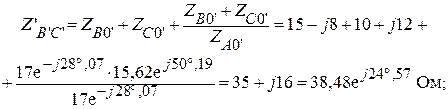
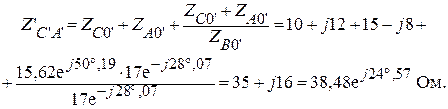
Находим общие фазные сопротивления двух параллельно включенных треугольников.

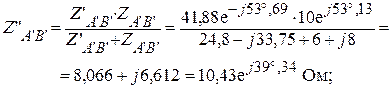
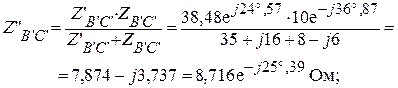
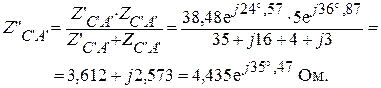
Согласно вычислениям, получили приведенную схему треугольник рис.2:

Рис. 2

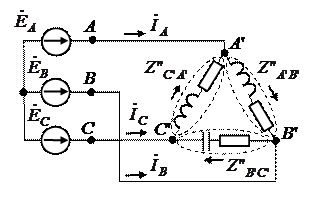Приведенный треугольник сопротивлений, преобразуем в звезду сопротивлений.

Рис. 3

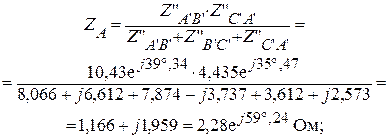
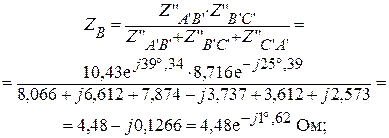
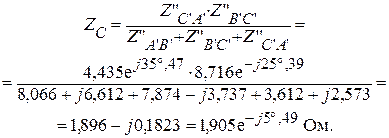
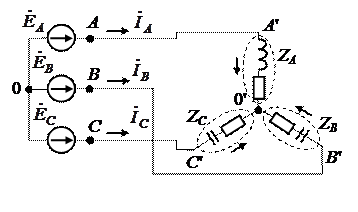Согласно вычислениям, получили приведенную схему звезда рис.3:

Вычислим соответствующие проводимости ветвей звезды.

;

;

.

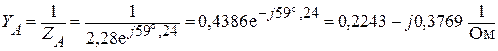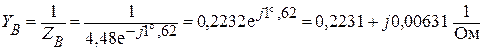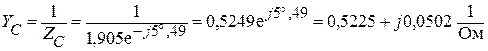Ищем напряжение смещения нейтрали.

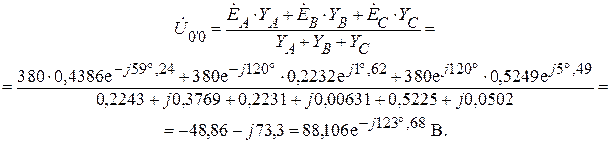
Находим линейные токи приведенной схемы звезда.

;

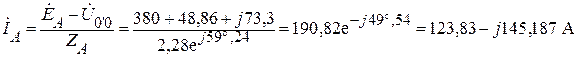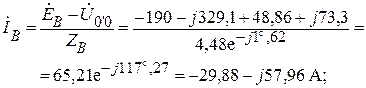
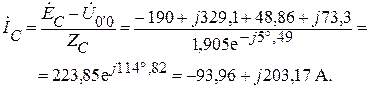
Выполним проверку по первому закону Кирхгофа.

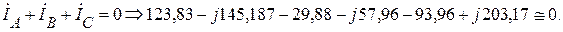
Находим линейные напряжения приведенной схемы звезда.

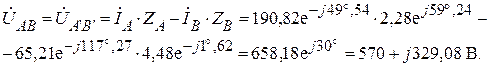
Или

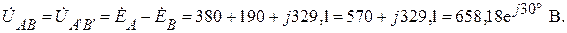
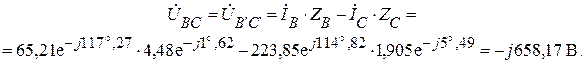
Или

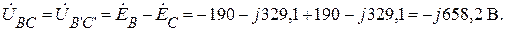
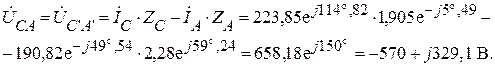
Или

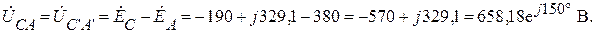
Находим фазные токи нагрузки треугольник рис.1:

;

;

.

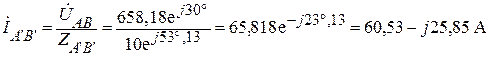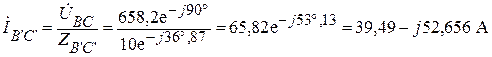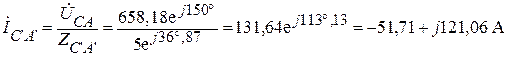Фазные токи нагрузки звезда рис.1 находим из первого закона Кирхгофа.

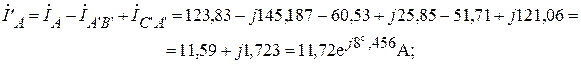
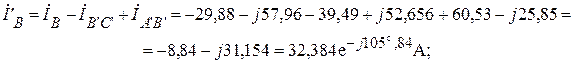
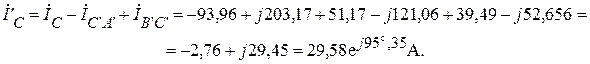
Фазные токи нагрузки звезда могут быть также найдены из системы уравнений, составленной по второму и первому законам Кирхгофа.

.

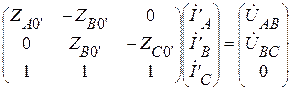В этом случае линейные токи 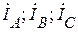для соответствующих узлов схемы рис.1, легко найти из первого закона Кирхгофа по известным фазным токам нагрузок треугольник и звезда:

; ; .

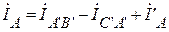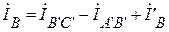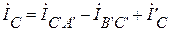Баланс мощностей.

Комплексная мощность.

	*		*		*

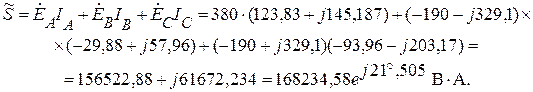
Активная мощность.

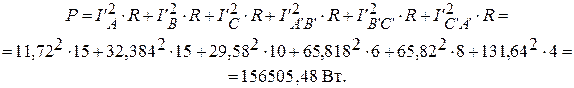
Реактивная мощность (без j).

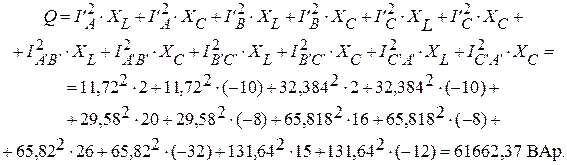
Расхождения в вычислениях незначительные.

Рис. 4

B, B '

A, A '

C, C '

0'

j

+

Строим векторную диаграмму рис.4 (масштаб произвольный).