Основные понятия и формулы

Несобственные интегралы

с бесконечными пределами ( первого рода )

Основные понятия и формулы

Если функция 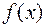определена и непрерывна на промежутке 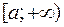, то

.

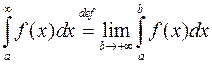Если существует конечный предел в правой части формулы (7.1), то говорят, что несобственный интеграл сходится, если этот предел бесконечен или не существует, то несобственный интеграл расходится.

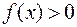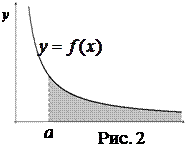
Если при 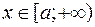и несобственный интеграл сходится, то он равен площади фигуры ограниченной ось 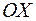, графиком функции и прямой 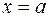(рис. 2)

.

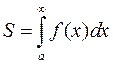Аналогично

,

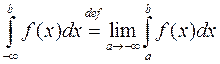если 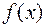определена и непрерывна на промежутке 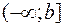и

,

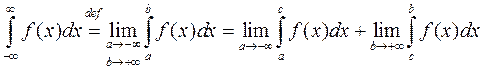если 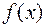определена и непрерывна на промежутке .

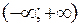Ниже приводятся признаки сходимости несобственных интегралов вида. Для несобственных интегралов вида и они формулируются аналогично.

1) Обобщенная формула Ньютона-Лейбница.

Если 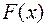- первообразная для 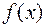и существует конечный предел 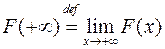, то интеграл (7.1) сходится и

.

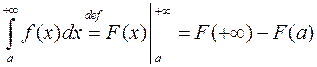Если же конечный 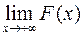не существует, то интеграл расходится.

2) Признак сравнения.

Пусть 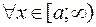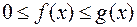. Если интеграл 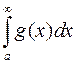сходится, то сходится и интеграл 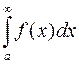. Если интеграл 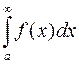расходится, то расходится и интеграл .

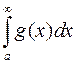3) Предельный признак сравнения.

Есл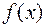и и 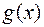положительные функции одного порядка при 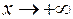, то есть 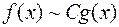, где 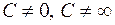(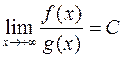), то интегралы 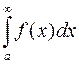и 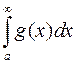сходятся или расходятся одновременно.

Замечание. При использовании признаков сравнения полезно иметь ввиду интеграл

(),

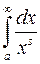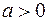сходящийся при 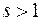и расходящийся при .

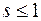4) Абсолютная сходимость.

Если сходится интеграл 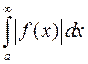, то сходится и интеграл 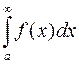, (в этом случае говорят, что он сходится абсолютно).

1. Исследовать сходимость несобственного интеграла .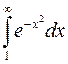

◄ Применим признак сравнения. Пр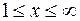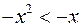и и 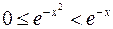. Интеграл 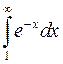сходится (см. задачу 11.2.1), поэтому сходится и интеграл . ►

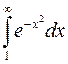2. Исследовать сходимость несобственного интеграла .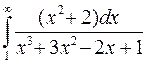

◄ Применим предельный признак сравнения. В числителе и знамена-

теле дроби 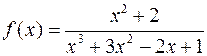сохраним только слагаемые с наибольшими степенями – “главные” при 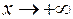. Получим функцию 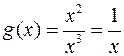, эквивалентную 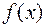: 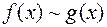. Это можно проверить и непосредственно по определению эквивалентности:

.

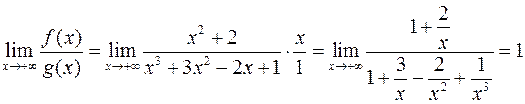Так как несобственный интеграл 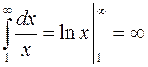- расходится, то расходится и интеграл . ►

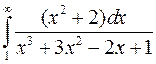i. Исследовать сходимость несобственного интеграла .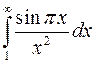

◄ Так как 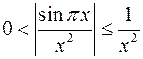, а интеграл 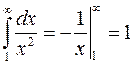сходится, то по

признаку сравнения сходится и интеграл 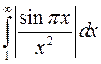. Но это означает, что 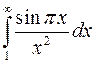сходится абсолютно. ►

Замечание. В примерах 11.2.5 и 11.2.6 мы могли не вычислять интегралы 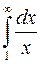и 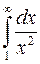, а просто сослаться на то, что они являются частными случаями стандартного интеграла при 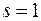(расходящегося) и 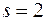(сходящегося).