Статистическая проверка гипотез
| Нулевая гипотеза Н0 | Результаты решения относительно нулевой гипотезы Н0 | |
| отклонена | принята | |
| верна | ошибка первого рода, ее вероятность Р(Н1/Н0) = α | правильное решение, его вероятность Р(Н0/Н0) = 1 - α |
| не верна | правильное решение, его вероятность Р(Н1/Н1) = 1 - β | ошибка второго рода, ее вероятность Р(Н0/Н1) = β |
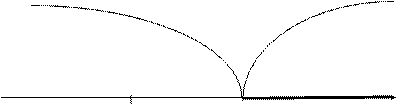 |
Область допустимых Критическая
значений область
К
0 Ккр.
Рис 1. Правосторонняя критическая область.
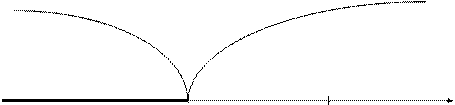 |
Критическая Область допустимых
область значений
К
-Ккр. 0
Рис 2. Левосторонняя критическая область.
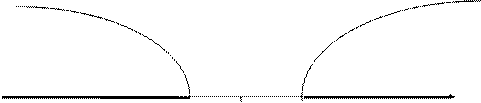 |
Критическая Область допустимых Критическая
область значений область
К
-Ккр. 0 Ккр.
Рис 3. Двусторонняя критическая область.
Проверка гипотезы о значении генеральной средней (математического ожидания) при известной генеральной дисперсии
| Нуль-гипотеза | 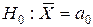 |
| Альтернативная гипотеза | а) 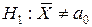 б) б) 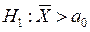 в) в) 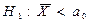 |
| Уровень значимости для критерия | 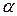 (часто (часто 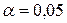 или или 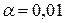 ) ) |
| Критерий (критериальная статистика) | 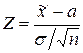 (предполагается, что (предполагается, что 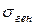 известно) известно) |
| Критические точки | Зависят от 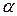 . Это: а) границы . Это: а) границы 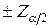 , разделяющие критические области принятия , разделяющие критические области принятия 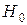 (когда (когда 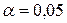 , критические точки , критические точки 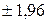 ; когда ; когда 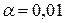 , критические точки , критические точки 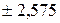 . Для других значений . Для других значений 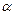 критические точки могут быть получены из таблицы функции Лапласа) критические точки могут быть получены из таблицы функции Лапласа) |
| Критические точки | б) Граница 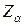 , разделяющая критическую область от области принятия , разделяющая критическую область от области принятия  находится как находится как 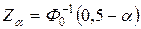 . (когда . (когда 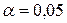 критическая точка критическая точка 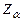 =1,645; когда =1,645; когда 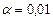 критическая точка критическая точка 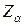 =2,325) в) граница - =2,325) в) граница - 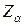 , разделяющая критическую область от области принятия , разделяющая критическую область от области принятия 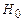 находится как - находится как - 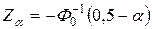 (когда (когда 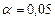 критическая точка - критическая точка - 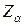 =-1,645; когда =-1,645; когда 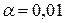 критическая точка - критическая точка - 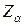 =-2,325) =-2,325) |
| Правило принятия решения | 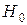 отклоняется: а) если отклоняется: а) если 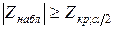 б) если б) если 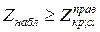 в) если в) если 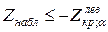 |
6. Проверка гипотезы о значении генеральной средней (математического ожидания) при неизвестной генеральной дисперсии
| Нуль-гипотеза | 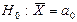 | |
| Альтернативная гипотеза | а) 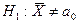 б) б) 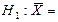 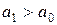 в) в) 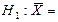 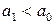 | |
| Уровень значимости для критерия | 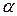 (часто (часто 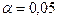 или или 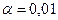 ) ) | |
| Критерий (критериальная статистика) | 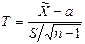 (предполагается, что (предполагается, что 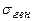 неизвестно). Если объем выборки неизвестно). Если объем выборки 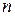 достаточно велик, то логично применить критерий достаточно велик, то логично применить критерий 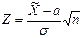 , в котором следует положить , в котором следует положить 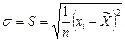 | |
| Критические точки | Зависят от 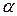 . Это: а) границы . Это: а) границы 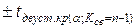 , разделяющие критические области от области принятия , разделяющие критические области от области принятия 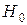 ; определяются по таблице распределения Стьюдента по заданному уровню значимости ; определяются по таблице распределения Стьюдента по заданному уровню значимости 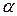 , помещенному в верхней строке таблицы и числу степеней свободы , помещенному в верхней строке таблицы и числу степеней свободы 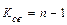 б) граница б) граница 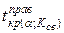 , разделяющая правостороннюю критическую область от области принятия , разделяющая правостороннюю критическую область от области принятия 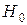 , определяются по уровню значимости , определяются по уровню значимости  , помещенному в нижней строке таблицы и числу степеней свободы , помещенному в нижней строке таблицы и числу степеней свободы 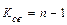 | |
| Критические точки | в) граница - 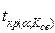 , разделяющая левостороннюю критическую область от области принятия , разделяющая левостороннюю критическую область от области принятия 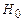 определяется сначала определяется сначала 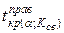 и затем полагается и затем полагается 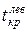 =- =- 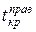 . . | |
| Правило принятия решения | 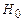 отклоняется: а) если отклоняется: а) если 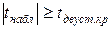 б) если б) если 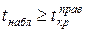 в) если в) если 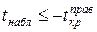 | |
 2015-10-13
2015-10-13 3866
3866