1. Вектор 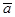 имеет длину, равную 4, и составляет с координатными осями следующие углы: с осью
имеет длину, равную 4, и составляет с координатными осями следующие углы: с осью 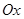 —
— 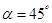 , с осью
, с осью 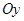 —
— 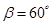 , с осью
, с осью 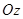 —
— 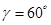 . Вычислить проекции вектора
. Вычислить проекции вектора 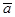 на координатные оси.
на координатные оси.
2. Даны точки 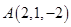 ,
, 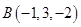 ,
, 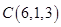 ,
, 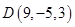 . Вычислить
. Вычислить 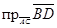 .
.
3. Векторы 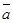 и
и 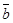 образуют угол
образуют угол 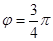 . Зная, что
. Зная, что 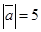 ,
, 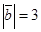 , вычислить
, вычислить 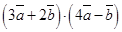 .
.
4. Даны вершины треугольника 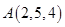 ,
, 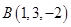 ,
, 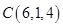 . Найти площадь треугольника
. Найти площадь треугольника 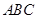 .
.
5. Определить, при каких значениях 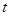 векторы
векторы 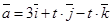 ,
, 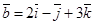 ,
, 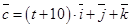 компланарны.
компланарны.
6. Дано: 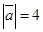 ,
, 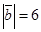 . Определить, при каком значении
. Определить, при каком значении 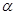 векторы
векторы 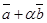 ,
, 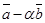 будут взаимно перпендикулярными.
будут взаимно перпендикулярными.
7. Даны четыре точки 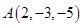 ,
, 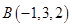 ,
, 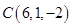 ,
, 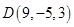 . Определить, лежат ли точки A, B, C, D в одной плоскости.
. Определить, лежат ли точки A, B, C, D в одной плоскости.
8. Упростить выражение 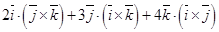 .
.
9. Векторы 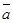 и
и 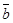 образуют угол
образуют угол 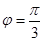 . Зная, что
. Зная, что 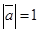 ,
, 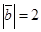 , вычислить
, вычислить 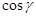 ,
, 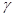 — угол между векторами
— угол между векторами 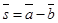 и
и 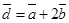 .
.
10. Найти объем пирамиды с вершинами 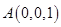 ,
, 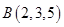 ,
, 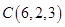 ,
, 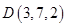 .
.
11. Определить, при каких значениях 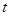 векторы
векторы 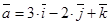 ,
, 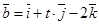 ,
, 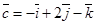 образуют левую тройку.
образуют левую тройку.
12. Векторы 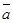 и
и 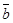 образуют угол
образуют угол 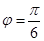 . Зная, что
. Зная, что 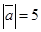 ,
, 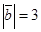 , вычислить
, вычислить 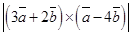 .
.
13. Даны три вектора 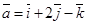 ,
, 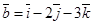 ,
, 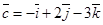 . Найти
. Найти 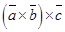 .
.
14. Вычислить площадь параллелограмма, построенного на векторах 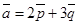 и
и 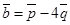 , где
, где 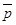 и
и 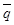 — перпендикулярные друг другу орты.
— перпендикулярные друг другу орты.
15. Найти единичный вектор, перпендикулярный одновременно оси абсцисс и вектору 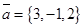 .
.
 2015-10-14
2015-10-14 400
400






