Задачи для подготовки к контрольной работе

1. Найти Ах, если вектор , а оператор А имеет матрицу 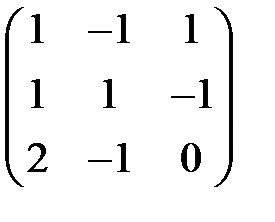в базисе .

2. Проверить линейность, найти ядро, образ, ранг, дефект, матрицу, найти собственные векторы и собственные значения, проверить, является ли оператор оператором простой структуры, если является, найти базис, в котором матрица оператора диагональна и записать эту диагональную матрицу и формулу A’=S^-1AS, найти S, выяснить, существует ли обратный:

А) Оператор А переводит R³в себя, первые два базисных вектора растягивает в 2 раза, последний сохраняет;

Б) Оператор А переводит R² в себя, действует на базисных векторах по формулам: A i = j, A j = i;

В) Оператор А – оператор поворота на угол π/6 в положительном направлении в плоскости R²;

Г).Ах=λх в R³;

Д).Ах=λx+ a в R³, -фиксированный вектор;

Е). А- ортогональное проектирование на плоскость

Ж). А- ортогональное проектирование на прямую

З).А- ортогональное проектирование на плоскость параллельно вектору ;

И). А- проектирование на прямую параллельно плоскости ;

К). А- зеркальное отражение относительно плоскости 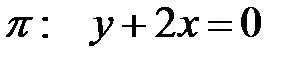, (т.е. любая точка переходит в симметричную

относительно плоскости);

Л). А- зеркальное отражение относительно прямой 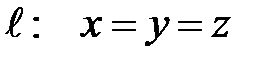(т.е. любая точка переходит в симметричную

относительно прямой);

М). 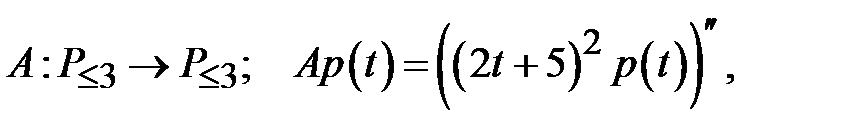базис:

Н). 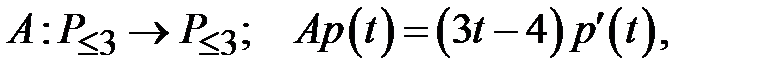базис:

О). 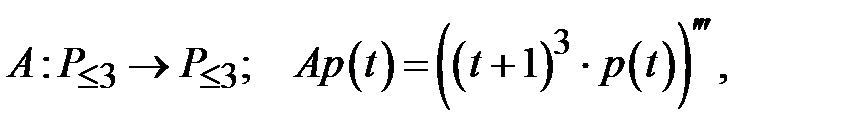базис:

П). -множество матриц 2х2, базис-стандартный.

Р). 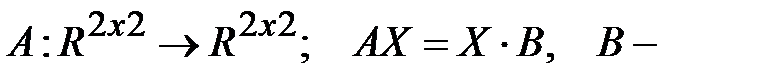фиксированная матрица из .

С). .

Т). .

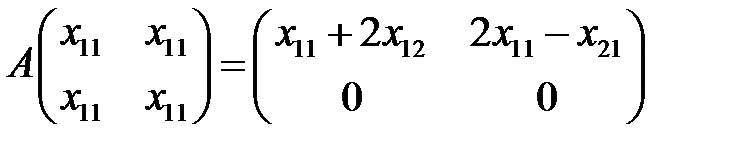У).

Ф).

Х).

Ц). 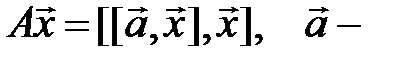фиксированный вектор.

Ш). 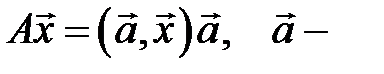фиксированный вектор.

Щ). А: R³ -> R³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .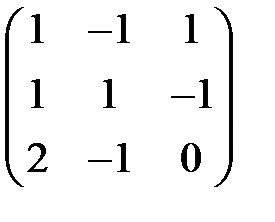

Ъ). А: R³ -> R³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .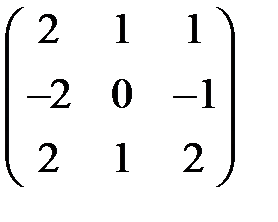

Ы). А: С³ -> С³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .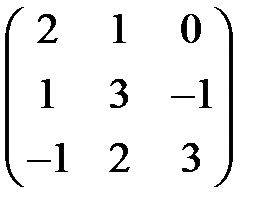

Ь). А: С³ -> С³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .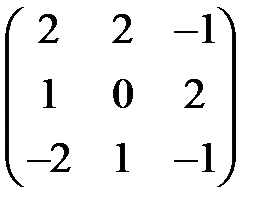

Э). А: С³ -> С³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .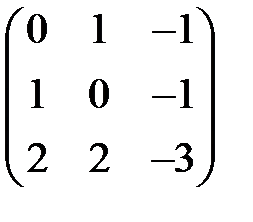

Ю). А: R³ -> R³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .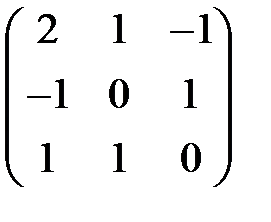

Я). А: R³ -> R³, имеет в некотором базисе е₁,е₂,е₃ матрицу: .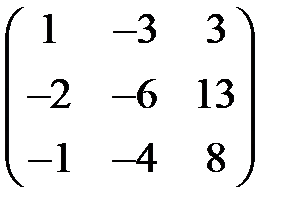

3. Найти собственные значения и собственные векторы преобразования, являющегося дифференцированием пространстве многочленов степени не выше n.

4. Оператор имеет матрицу 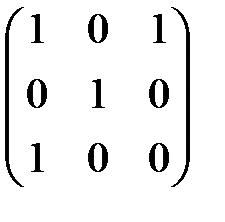в базисе: . Найти матрицу этого оператора в базисе

.

5. Оператор имеет матрицу 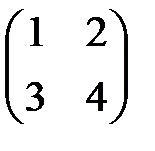в базисе: . Найти матрицу этого оператора в базисе .

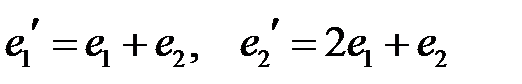6. Оператор имеет матрицу 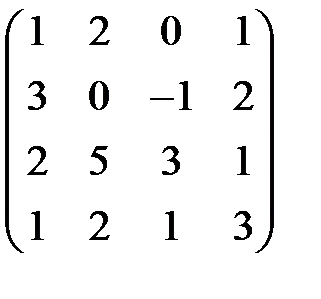в базисе: . Найти матрицу этого оператора в базисах и .

7. Оператор имеет матрицу 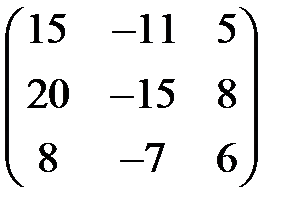в базисе: . Найти матрицу этого оператора в базисе .

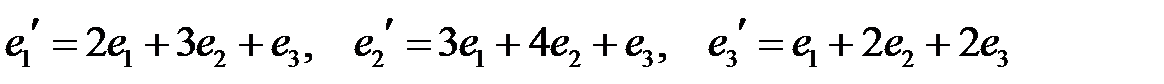8. Доказать, что существует единственное линейное преобразование пространства R³, переводящее данные линейно независимые вектора в вектора . Координаты векторов даны в базисе .Доказать, что матрица этого оператора в произвольном базисе (е) равна произведению 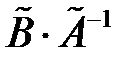, где - матрицы, столбцы которых являются координатами векторов, соответственно и в базисе (е).

9. Линейный оператор С равен произведению операторов А и В (сначала выполняется линейный оператор А, потом - линейный оператор В). Найти матрицы операторов А, В, С. Существует ли оператор, обратный оператору С? Если существует, описать его действие, если не существует, объяснить, почему. Все операторы действуют в R³.

а). A- поворот вокруг оси OZ на 90 градусов, В- проекция на плоскость XOZ;

б). А- зеркальное отражение относительно плоскости XOY, В-гомотетия с коэффициентом к=2;

в).А-зеркальное отражение относительно оси OZ, В- векторное умножение на вектор ;

г). А- поворот пространства на угол 120 градусов вокруг прямой x=y=z, В- проектирование на ось ОХ.

10. Проскуряков, №№ 1498-1501,1504-1505,1465-1474, 1479-1482 (часть этих задач относится к бонусным).

Бонусные задачи могут быть такого типа:

1. Доказать, что собственные значения оператора А^-1 равны (с учетом кратности) обратным величинам собственных значений оператора А.

2. Доказать, что сумма собственных значений оператора равна следу его матрицы, а произведение собственных значений равно определителю матрицы.

3. Доказать, что собственные значения оператора А^к равны к-ым степеням собственных значений оператора А.

4. Доказать, что размерность собственного подпространства, соответствующего собственному значению λ₀ не превосходит кратности корня λ₀ в характеристическом многочлене оператора. Привести пример оператора, для которого это неравенство – строгое.

5. Доказать, что в R³ любой оператор имеет собственный вектор.

6. Доказать, что если подпространство инвариантно относительно оператора А:LàL, имеющего обратный оператор, то это подпространство инвариантно и относительно оператора А^-1.

7. Доказать, что если U и V -подпространства пространства L, такие, что сумма их размерностей совпадает с размерностью всего пространства L, то найдется линейный оператор A: L ---> L, такой, что его ядро совпадает с подпространством U, а его образ совпадает с подпространством V.

8. Дано: операторы А и В отображают линейное пространство L в себя, dimL=n. Доказать, что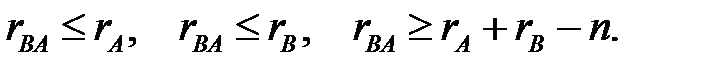

9. Доказать, что матрица произведения операторов А и В равна произведению матриц операторов А и В.

10. Доказать, что любое линейное преобразование пространства R¹ сводится к умножению всех векторов на одно и то же число α, Ax=αx.

11. Показать, что любые два оператора А и В, отображающие линейное пространство Х в линейное пространство Н линейно независимы, если области их значений пересекаются только по нулю.

12. Доказать, что если dimL=1, то dim£(L)=1.

13. Другие несложные утверждения, доказанные на лекциях.