| Настройки | Значение |
| Тип | Тест с оценкой |
| Всего вопросов | |
| Всего баллов | |
| Проходной балл | 3баллов |
| Показать вопросы | Все |
| Перемешивать вопросы | Да |
| Показать экран с результатами Если тест пройден | Да |
| Показать экран с результатами Если тест провален | Да |
| Ограничение по времени | 0:20:0 |
| 1. В треугольнике со сторонами a, b, c расстояние от вершины А до точек касания вписанной окружностью сторон, содержащих эту вершину, равно: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 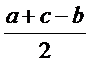
| |
| () | 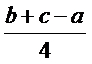
| |
| () | 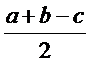
| |
| (+) | 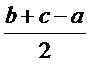
|
| 2. Проекция боковой стороны равнобедренной трапеции на большее основание равна: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | полусумме оснований | |
| (+) | полуразности оснований | |
| () | полуразности боковых сторон | |
| () | полусумме боковых сторон |
| 3. Центр окружности, описанной около трапеции, лежит на пересечении … (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | биссектрис углов трапеции | |
| () | диагоналей трапеции | |
| (+) | серединных перпендикуляров к сторонам трапеции | |
| () | диагоналей и биссектрис углов трапеции |
| 4. Центр окружности, вписанной в треугольник, является точкой пересечения его … (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | серединных перпендикуляров | |
| () | медиан | |
| () | высот | |
| (+) | биссектрис |
| 5. Укажите формулу расчета радиуса описанной окружности около треугольника: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 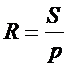
| |
| (+) | 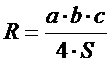
| |
| () | 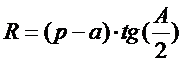
| |
| () | 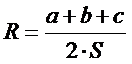
|
| 6. Какая из записей не является формулой для расчета площади треугольника: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | 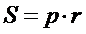
| |
| () | 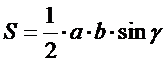
| |
| (+) | 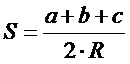
| |
| () | 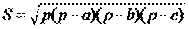
|
| 7. Какая из приведенных формул является формулой площади параллелограмма: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 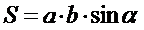
| |
| () | 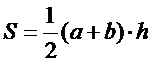
| |
| () | 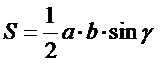
| |
| () | 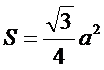
|
| 8. Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | квадрату суммы секущей и ее внешней части | |
| () | квадрату произведения секущей на ее внешнюю часть | |
| () | сумме секущей и ее внешней части | |
| (+) | произведению секущей на ее внешнюю часть |
| 9. Если две хорды окружности пересекаются в одной точке, то верно следующее утверждение: (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| () | разница отрезков одной хорды равна разнице отрезков другой хорды | |
| (+) | произведение отрезков одной хорды равно произведению отрезков другой хорды | |
| () | сумма отрезков одной хорды равна сумме отрезков другой хорды | |
| () | отношение отрезков одной хорды равно отношению отрезков другой хорды |
| 10. Радиус, перпендикулярный хорде, делит хорду в отношении… (Тип: Одиночный выбор, Баллов: 1, Попыток: 1) | ||
| (+) | 1:1 | |
| () | 1:2 | |
| () | 1:3 | |
| () | 2:3 |
 2015-10-13
2015-10-13 152
152






