ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
УЧЕБНО-МЕТОДИЧЕСКОЕ ПОСОБИЕ
Йошкар-Ола, 2014
Рецензенты:
Рекомендовано к изданию редакционно-издательским советом МарГУ
Н.И.Попов, Е.Н.Никифорова.
Элементы линейной и векторной алгебры: учебно-методическое пособие/ Мар.гос.ун-т; Н.И.Попов, Е.Н.Никифорова. – Йошкар-Ола, 2014. - с.
Учебно-методическое пособие предназначено для студентов вузов, обучающихся по направлениям подготовки «Агрономия», «Агроинженерия», «Зоотехния», «Технология производства и переработки сельскохозяйственной продукции», «Продукты питания животного происхождения», «Товароведение» и изучающих элементы линейной и векторной алгебры в курсе высшей математики. В пособии приведены необходимые теоретические сведения и формулы, даны решения типовых задач, в конце каждого параграфа помещены задачи для самостоятельного решения с указанием ответов. Книга может использоваться при самостоятельной работе студентами-заочниками.
ВВЕДЕНИЕ
Мотивацией подготовки данного учебно-методического пособия явилось то, что в настоящее время в условиях перехода к Федеральным государственным образовательным стандартам нового поколения ощущается нехватка учебников по разделу высшей математики «Линейная и векторная алгебра», доступных для студентов агроинженерных и других, связанных с подготовкой специалистов для сельского хозяйства, направлений подготовки. Вышедшие из печати в последнее время учебники и пособия по указанному разделу высшей математики ориентированы в основном на студентов технических вузов и предполагают достаточно высокий уровень их математической подготовки.
Данное учебно-методическое пособие предназначено для студентов вузов, обучающихся по направлениям подготовки «Агрономия», «Агроинженерия», «Зоотехния», «Технология производства и переработки сельскохозяйственной продукции», «Продукты питания животного происхождения», «Товароведение» и изучающих элементы линейной и векторной алгебры в курсе высшей математики. В пособии приведены необходимые теоретические сведения и формулы, даны решения типовых задач, в конце каждого параграфа помещены задачи для самостоятельного решения с указанием ответов.
Книга может использоваться при самостоятельной работе студентами-заочниками. В литературе, список которой приведен в конце книги, можно найти дополнительные сведения по разным вопросам линейной и векторной алгебры.
Глава 1. Элементы линейной алгебры
Матрицы. Основные понятия. Действия над матрицами
Матрицей размера 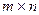 или
или 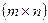 - матрицей называется прямоугольная таблица чисел
- матрицей называется прямоугольная таблица чисел
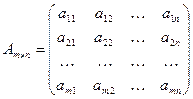 , (1.1)
, (1.1)
состоящая из 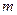 строк и
строк и 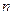 столбцов. Если
столбцов. Если 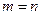 , то матрица называется квадратной.
, то матрица называется квадратной.
Используют сокращенную запись 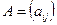 ,
, 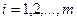 ,
, 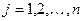 . Наряду с круглыми скобками применяют и другие обозначения матрицы:
. Наряду с круглыми скобками применяют и другие обозначения матрицы: 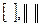 .
.
Матрица 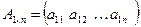 называется матрицей (вектором)- строкой, а матрица
называется матрицей (вектором)- строкой, а матрица 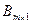 , состоящая из одного столбца – матрицей (вектором)- столбцом:
, состоящая из одного столбца – матрицей (вектором)- столбцом:
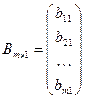 .
.
Элементы матрицы 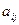 , у которых номер столбца равен номеру строки
, у которых номер столбца равен номеру строки 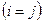 , называются диагональными и образуют главную диагональ матрицы. Матрица
, называются диагональными и образуют главную диагональ матрицы. Матрица 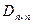 , у которой все недиагональные элементы равны нулю, называется диагональной.
, у которой все недиагональные элементы равны нулю, называется диагональной.
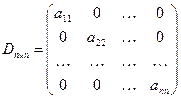 .
.
Квадратная диагональная матрица называется единичной, если все ее диагональные элементы равны единице:
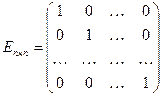 .
.
Матрица, все элементы которой равны нулю,называется нулевой матрицей:
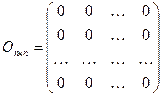 .
.
Две матрицы 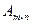 и
и 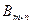 одинаковой структуры равны, если они совпадают поэлементно, т.е
одинаковой структуры равны, если они совпадают поэлементно, т.е 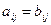 . Над матрицами можно производить ряд операций:
. Над матрицами можно производить ряд операций:
1. Произведением матрицы 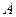 на число
на число 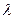 называется матрица, элементы которой определяются равенством
называется матрица, элементы которой определяются равенством 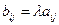 .
.
2. Суммой 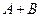 матриц
матриц 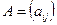 и
и 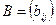 одного порядка называется матрица
одного порядка называется матрица 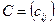 того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц
того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц 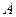 и
и 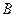 , т.е.
, т.е. 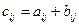 , где
, где 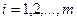 ,
, 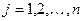 . В частности,
. В частности, 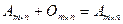 .
.
3. Разность двух матриц определяется соотношением:
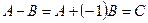 , где
, где 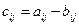 .
.
4. Произведение 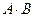 матрицы
матрицы 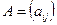 размера
размера 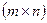 на матрицу
на матрицу 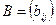 размера
размера 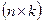 , называется матрица
, называется матрица 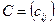 размера
размера 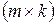 , элементы которой определяются равенством
, элементы которой определяются равенством
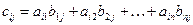 . (1.2)
. (1.2)
Свойства, кроме коммутативного закона умножения, используемые при операциях над действительными числами, справедливы и для операций над матрицами.
5. Квадратные матрицы можно возводить в целую положительную степень 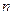 , т.е.
, т.е. 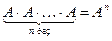 .
.
6. Следом квадратной матрицы 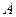 называется сумма ее диагональных элементов:
называется сумма ее диагональных элементов: 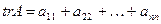 .
.
7. Транспонированием матрицы называется переход от матрицы 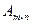 к матрице
к матрице 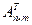 , в которой строки и столбцы меняют местами с сохранением порядка
, в которой строки и столбцы меняют местами с сохранением порядка 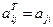 .
.
Свойства операций транспонирования матриц:
1) 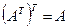 ; 3)
; 3) 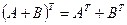 ;
;
2) 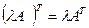 ; 4)
; 4) 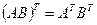 .
.
Задача 1.1. Найти произведение матриц 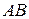 и
и 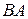 ,если
,если
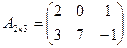 ,
, 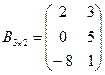 .
.
Решение. 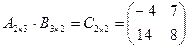 .
.
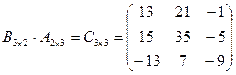 , получаем, что
, получаем, что  .
.
Задача 1.2. Возвести матрицу 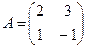 в степень
в степень 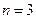 и найти след
и найти след
матрицы 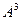 .
.
Решение. 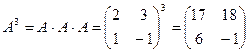 ,
, 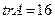 .
.
Задача 1.3. Найти линейную комбинацию матриц 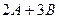 ,
,
где 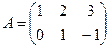 ,
, 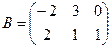 .
.
Решение. 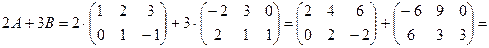
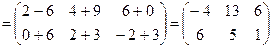 .
.
Задача 1.4. Найти значение матричного многочлена 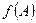 , если
, если
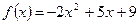 ,
, 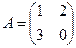 .
.
Решение. 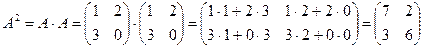 ,
,
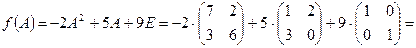
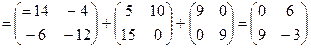 .
.
 2015-10-14
2015-10-14 360
360






