Предмет и аксиомы статики

Статикой называется раздел теоретической механики, изучающий общие свойства сил и условия равновесия твердых тел, находящихся под действием приложенных к ним сил.

Под равновесием твердого тела в статике понимается состояние его покоя по отношению к системе координат, принимаемой за неподвижную. За такую систему в статике можно принять систему координат, жестко связанную с Землей.

В основании статики помимо первого и третьего основ­ных законов классической механики лежит еще несколько подтверждаемых многовековой практикой положений, на­зываемых аксиомами статики. Опираясь на них, логиче­ским путем строятся все остальные положения статики. Условимся предварительно о следующих определениях.

1. Совокупность сил, действующих на данное тело, на­зывается системой сил. Силы, входящие в состав данной системы, называются составляющими этой системы.

2. Если система сил такова, что под ее действием сво­бодное тело не изменяет своего движения или, в частности, продолжает оставаться в покое, то такая система сил называется уравновешенной системой. О силах такой си­стемы говорят, что они находятся в равновесии.

Под «свободным» телом принимается тело, не скреплен­ное с другими телами, т. е. тело, которому можно сообщить любое перемещение в пространстве.

3. Сила, которая, будучи присоединена к некоторой системе сил, действующих на тело, приводит систему к равновесию, называется уравновешивающей данной системы сил. Очевидно, что в уравновешенной системе каждая из сил является уравновешивающей по отношению ко всем остальным.

4. Лее системы сил называются эквивалентными, если они оказывают одинаковое механическое действие на одно и то же свободное твердое тело.

5. Одна сила, эквивалентная данной системе сил, назы­вается равнодействующей этой системы.

6. Силы, действующие на данное тело со стороны других тел, называются внешними силами. Силы взаимодействия между частицами данного тела называются внутренними силами.

Первая аксиома. Абсолютно твердое тело на­ходится в равновесии под действием двух сил тогда и только тогда, когда эти силы равны по модулю и направлены по одной прямой в противоположные стороны.

Необходимо иметь в виду, что данная аксиома, как и все вообще положения статики, безоговорочно применима только к абсолютно твердому телу. При применении же ее к реальным деформируемым телам необходимо учиты­вать особенности сил и тел, к которым они приложены.

Рис. 3.

Если, например, мы приложим две равные по модулю и противоположные по направлению силы F₁ и F₂ к кон­цам гибкой нити, то она будет находиться в равновесии только при способе приложения этих сил, показанном на рис. 3, а (когда нить растягивается). При способе же при­ложения этих сил, показанном на рис. 3, б, нить сомнется и не будет находиться в равновесии. Если же вместо нити мы возьмем твердый стержень, то в обоих случаях, изобра­женных на рис. 3, он будет находиться в равновесии.

Вторая аксиома. Не нарушая действия данной системы сил на абсолютно твердое тело, можно добавить к этой системе сил или исключить из нее любую уравнове­шенную систему сил.

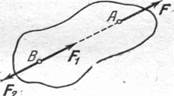Другими словами, присоединяя к данной системе сил, действующих на твердое тело, любую уравновешенную систему сил, мы получаем систему, эквивалентную данной. Наоборот, если в состав данной системы входит несколько сил, образующих в отдельности уравновешенную группу, то можно отбросить такую группу сил. Оставшаяся система эквивалентна данной. Доказательство. Пусть на тело действует сила F, приложенная в точке А (рис. 4). Возьмем на линии действия этой силы какую-нибудь произвольную точку В и приложим к ней две силы F_t и F₂, равные по модулю силе F (F = F₁ = F₂) и действующие по одной с ней прямой АВ в противоположные стороны. Силы F₁ и F₂ равны по модулю и направлены противоположно. По первой аксиоме статики они взаимно уравновешиваются; следовательно, на основании второй аксиомы от их присоединения состояние абсолютно твердого тела не изменится. Но силы F₁ и F₂ также взаимно уравновешиваются (на основании первой Рис.4.

аксиомы), и их поэтому можно отбросить, не изменяя состояния абсолютно твердого тела. Остается одна сила F₂ равная данной силе F и лежащая на линии ее действия. Так как точка приложения силы F₁ (точка В) была выбрана на линии действия данной силы произвольно, то аксиома доказана.

Следствие первое. Всякую силу, приложенную в какой-либо точке абсолютно твердого тела, можно, не изменяя ее действия, переносить в любую другую точку, лежащую на линии действия этой силы.

Мы видим, что для абсолютно твердого тела точка при­ложения перестает быть существенным элементом силы, ее заменяет линия действия силы. Вспоминая сказанное о типах векторов (стр. 22), можно заметить, что сила, при­ложенная к абсолютно твердому телу, является скользящим вектором.

Таким образом, действие силы на абсолютно твердое тело определяется следующими элементами: 1) модулем, 2) линией действия и 3) направлением силы по линии ее действия. Конечно, в каждом отдельном случае можно при­писать силе и некоторую точку приложения, но эта точка всегда может быть заменена другой точкой, лежащей на линии действия силы.

Необходимо заметить, что присоединение и отбрасыва­ние уравновешенных сил, так же как и перенос силы вдоль линии ее действия, изменяют картину распределения вну­тренних сил в теле. Так, например, изменение расположе­ния сил, приложенных к концам стержня, изображенного на рис. 3, а, в расположение, изображенное на рис. 3, б, может быть получено путем переноса сил F_x и F₂. вдоль их линий действия в соответственно противоположные концы стержня. Ясно, что такой перенос в случае дефор­мируемого стержня существенно изменяет его внутреннее состояние, так как в первом случае стержень растягивается, а во втором – сжимается.

В применении к реальным физическим телам данными приемами можно пользоваться только тогда, когда рас­сматривается лишь внешнее действие сил на данное тело, т. е. когда определяются лишь необходимые условия равно­весия этого тела. При рассмотрении этих условий мы при­нимаем тело за абсолютно твердое, и внутренние силы можно вообще не принимать во внимание. В самом деле, по закону равенства действия и противодействия любые две частицы тела действуют друг на друга с силами, равными по модулю и направленными по од­ной прямой в противоположные стороны. Следовательно, в своей совокупности эти силы всегда представляют уравновешенную систему, и в случае абсолютно твердого тела их можно отбро­сить.

Так как в статике рассмат­ривается равновесие именно аб­солютно твердых тел, то в дальнейшем под силами, действующими на тело, мы всегда будем понимать только внешние силы (если не будет сде­лано специальной оговорки).

Следствие второе. Равнодействующая и уравно­вешивающая силы равны по модулю и направлены по одной прямой в противоположные стороны.

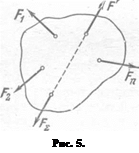
Доказательство. Положим, что сила F_Σ есть равнодействующая сил F₁, F₂,…, F_n. (рис. 5). Приложим по линии действия равнодействующей равную ей по мо­дулю, но направленную в противоположную сторону силу F'. Как силы, равные по модулю и противоположно на­правленные, силы F_Σ и F' взаимно уравновешиваются. ⁴ Не нарушая состояния тела, мы можем заменить рав­нодействующую F_Σ, ее составляющими, т. е. эквива­лентной ей системой сил F₁, F₂,…, F_n. А так как си­ла F' уравновешивает равнодействующую F_Σ, то она будет являться уравновешивающей и для системы сил.

Так как по условию сила F' равна по модулю и направ­лена противоположно силе F_Σ,, то требуемое положение доказано. Из данного следствия вытекает, что нахождение.

силы, уравновешивающей данную систему сил, можно свести к определению равнодействующей этой системы.

Третья аксиома. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и изображается диагональю параллелограмма, построен­ного на данных силах, как на сторонах.

Параллелограмм, построенный на данных силах, на­зывается параллелограммом сил, а сам способ нахождения равнодействующей путем построения параллелограмма на­зывается правилом параллелограмма.

Сложение сил, как и других векторных величин, по пра­вилу параллелограмма называют геометрическим (вектор­ным) сложением.

Геометрическое сложение сил, как и сложение любых векторов, обозначается обычным знаком сложения (+), стоящим между жирными буквами (или буквами со стрел­ками над ними), обозначающими силы.

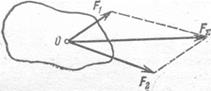
Если обозначить через F_Σ равнодей- ствующую двух сил F₁ и F₂, приложенных к одной точке О тела (рис. 6), то на основании данной аксиомы имеем

F_Σ = F₁ + F₂.

Рис.6

Если две силы приложены в различных точках тела, но линии их действия пересекаются, то, пользуясь следствием 1, мы можем перенести обе силы в точку пересечения их ли­ний действия и затем сложить по правилу параллелограмма. Если линии действия сил пересекаются где-либо вне тела, то, перенося обе силы в их точку пересечения и определив равнодействующую, нужно затем перенести ее по линии действия в одну из точек тела ¹).

') Последнее может оказаться невозможным, если линия дей­ствия равнодействующей пройдет вне тела. Но и в этом случае мы можем какую-либо точку, лежащую на линии действия равнодей­ствующей, связать (мысленно) неразрывным образом с телом и при­нять ее за точку приложения равнодействующей,

Четвертая аксиома (принцип отвер­девания). Если нетвердое тело находится в равновесии, то это равновесие не нарушится и в том случае, когда тело станет абсолютно твердым.

Аксиома очевидна, так как превращение находящегося в равновесии нетвердого деформируемого тела в абсолютно твердое тело может только еще более ограничивать возмож­ные движения тела, только еще более закреплять равно­весие тела, а не нарушать его.

Принцип отвердевания позволяет применять к любому нетвердому телу и к любой изменяемой конструкции усло­вия равновесия, устанавливаемые статикой для абсолютно твердого тела. Эти условия являются необходимыми усло­виями равновесия и для нетвердых тел, но не всегда доста­точными.

Как мы уже говорили выше, для равновесия гибкой нити недостаточно того, чтобы приложенные к ее концам силы были равны по модулю и направлены по одной пря­мой в противоположные стороны, нужно еще, чтобы они растягивали нить, а не сжимали.

Таким образом, учет деформаций, возникающих в реаль­ном теле под действием приложенных к нему сил, лишь дополняет результаты, полученные в механике абсолютно твердого тела, но не уничтожает их.

1.2. Связи и реакции связей

При решении большинства задач механики приходится иметь дело с телами несвободными, т. е. с такими, которые соприкасаются или скреплены с другими телами, благодаря чему становятся невозможными те или иные перемещения данного тела.

Если тело несвободно, то говорят, что на него наложены связи. Связями называются тела, ограничивающие свободу перемещения данного тела.

Так, для тела, лежащего на столе, связью является стол, для вала, лежащего в подшипниках, связями явля­ются подшипники, для лестницы, приставленной к стене, связями являются стена и пол.

Если под действием приложенных к нему сил тело будет давить на связь, то связь в свою очередь будет дей­ствовать на данное тело.

Сила, с которой связь действует на тело, препятствуя его перемещению в том или ином направлении, называется силой реакции (противодействия) этой связи.

По закону равенства действия и противодействия сила реакции связи равна по модулю силе давления на связь и направлена в сторону, противоположную этой силе, т. е. в сторону, противоположную тому направлению, в котором данная связь препятствует перемещению тела.

Все действующие на тело силы можно разделить на ак­тивные силы и силы реакции связей. К активным силам относятся все силы, не являющиеся реакциями связей.

В отличие от активных сил, сила реакции связи зависит как от других, действующих на данное тело сил, так и от движения тела и характера наложенных на него связей. Она существует лишь тогда, когда тело под действием прило­женных к нему активных сил оказывает давление на дан­ную связь. Если нет действия на связь, то не будет и проти­водействия связи (силы реакции связи).

Модуль силы реакции связи всегда заранее неизвестен. Направление этой силы заранее известно в том случае, когда данная связь может препятствовать движению тела лишь в одном определенном направлении. В противных случаях направление силы реакции связи также заранее неизвестно и оно определяется только в результате решения соответствующей задачи.

Задачи на равновесие несвободных тел решаются в ста­тике на основании следующего очевидного обстоятельства: всякое несвободное тело можно рассматривать как свобод­ное, если мысленно освободить его от связей и заменить их действие на тело силами реакций этих связей (принцип освобождаемости, или аксиома связей).

Пользуясь этим принципом, можно применять к несво­бодному телу условия равновесия, устанавливаемые в ста­тике для свободного тела. Нужно только в число сил, дей­ствующих на тело, обязательно включать и силы реакций отброшенных связей.

Большинство технических задач статики как раз и за­ключается в определении сил реакций связей. Зная их, мы будем знать и силы давления на связи, т. е. будем иметь данные, необходимые для расчета на прочность соответ­ствующих конструкций.

Рассмотрим, как определяется направление реакций не­которых основных типов связей.

1. Гладкая опорная поверхность. Гладкой называется поверхность, трением тела о которую можно пренебречь. Связи без трения относятся к так называемым идеальным свя­зям. Рассмотрением таких связей мы пока и ограничимся.

'Гак как гладкая опорная поверхность не препятствует скольжению по ней поверхности тела, то реакция R гладкой поверхности (рис. 7) направлена всег­да по общей нормали) к поверхности тела и поверхности связи в их точке касания. Нормалью к поверхности называется перпендикуляр к каса^ тельной плоскости, проведенный через точку касания,

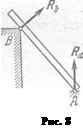
Если одна из соприкасающихся поверхностей имеет заострение (рис.8), то реакция должна быть направлена по нормали к другой. Например, к гладкому брусу АВ (рис. 8), опирающемуся в точке А на пол и в точке В на столб, приложены реакции R_a пола и R_b столба, направленные так, как это изображено на рисунке.

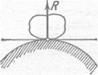Рис.7

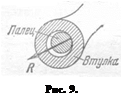2. Неподвижный цилиндрический шарнир или подшипник. Цилиндри­ческим шарниром называется соеди­нение двух тел посредством пальца (болта), проходящего через отверстия в этих телах. Диаметр отверстия во втулке (рис. 9) несколько больше диаметра пальца. Тело, жестко скреп­ленное с втулкой, может только вра­щаться вокруг оси шарнира (оси пальца), перпендикуляр­ной к плоскости рисунка.

Во многих случаях можно пренебречь трением в шар­нире (между поверхностями пальца и втулки). В таком шарнире (называемом «идеальным») нет препятствий ни для поворота втулки вокруг оси паль­ца, ни для ее перемещения вдоль этой оси. Идеальный шарнир препятствует лишь перемещению втулки в направ­лении нормали к поверхности втулки и пальца, и, следовательно, его реак­ция может быть направленной толь­ко по этой нормали (по радиусу паль­ца). Но так как втулка в зависимо­сти от ее расположения и приложенных к ней сил может прижиматься к любой точке пальца, то указать заранее направление реакции цилиндрического шарнира нельзя. Единственное, что можно утверждать (если пренебречь трением в шарнире), это то, что реакция неподвижного цилиндрического шарнира лежит в плоскости, перпендику­лярной к его оси, и имеет радиальное направление.

Для определения реакции связи в тех случаях, когда ее направление оказывается неопределенным, очень часто полезно заменить искомую реакцию несколькими состав­ляющими реакциями, неизвестными уже только по модулю. Например, реакции шарнира А (рис. 10, а) или упора А (рис. 10, б) удобно разложить на горизонтальную R₁ и вертикальную R₂ составляющие. В обоих случаях можно считать, что связь А (шарнир или упор) препятствует пере­мещению тела как в горизонтальном, так и в вертикальном направлениях.

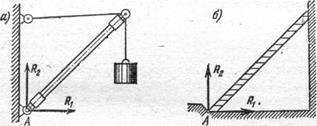
Рис. 10.

После того, как будут найдены модули каждой из со­ставляющих реакций, можно найти (при необходимости) и полную реакцию связи как равнодействующую ее со­ставляющих.

Заметим, что, разлагая реакцию на составляющие (в данных примерах на горизонтальную и вертикальную), можно не заботиться о правильности выбора направлений по намеченным линиям их действия. В случае, если в дей­ствительности та или иная составляющая окажется на­правленной в сторону, противоположную предложенной, мы будем (как это увидим дальше) получать для нее в от­вете отрицательное значение.

Шарнирно-неподвижная опора часто схематически изоб­ражается двумя стержнями (рис. 11, а и б), соединенными между собой на одном конце общим шарниром А, ось ко­торого, очевидно, будет неподвижной. Реакция такой опоры проходит через ось шарнира, но не известна ни по модулю, ни по направлению и, следовательно, характеризуется двумя неизвестными элементами.

Определение модуля и направления реакции шарнирно-неподвижной опоры можно, как было сказано выше, заме­пить определением модулей двух составляющих этой реак­ции. Наличие в схеме шарнирно-неподвижной опоры двух стержней указывает на то, что неизвестны два элемента реакции данной связи.

По ГОСТу 2.770-68 шарнирно-неподвижная опора для стержня изображается так, как показано на рис. 11.

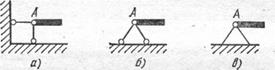
Рис. 11.

3. Опора на катках. Мы говорили до сих пор о связях, осуществляемых абсолютно гладкими поверхностями. Эти связи препятствуют перемещению тел только в направле­нии, нормальном к поверхности, и характеризуются одной нормальной реакцией. Негладкая поверхность не только препятствует перемещению, нарушающему связь, но и за­трудняет перемещение по самой поверхности. Следова­тельно, реакция негладкой поверхности имеет две состав­ляющие: одну – нормальную к поверхности, и другую – лежащую в плоскости скольжения.(в общей касательной плоскости к поверхности тела и опорной поверхности) и направленную в сторону, противоположную той, в которую двигают или пытаются сдвинуть тело. Первая составля­ющая является нормальной реакцией, вторая носит назва­ние силы трения. Следовательно, негладкие опорные по­верхности отличаются тем, что для них приходится допол­нительно учитывать силу трения.

О том, как это делается, мы будем говорить дальше, в главе о трении. Сейчас отметим только, что хотя идеально гладких поверхностей, а следовательно, и идеальных связей в действительности не существует, но на практике во мно­гих случаях силой трения можно пренебречь и практически считать связи идеальными.

Примером такой связи является часто применяемая опора на катках (рис. 12, а). Подвижность катка настолько велика и, следовательно, сила трения настолько мала, что можно считать данную связь препятствующей лишь перемещению, перпендикулярному к опорной плоскости, почему она и характеризуется всегда лишь одной нормальной реакцией.

Опора на катках не препятствует перемещению оси шарнира параллельно опорной плоскости и представляет собой так называемую шарнирно-подвижную опору.

Такая опора часто схематически изображается одним стержнем с шарниром на конце (рис. 12, б). Реакция по­добной опоры проходит через ось шарнира и направлена

по нормали к опорной поверхности. Наличие в схеме опоры одного стержня указывает на то, что неизвестен лишь один элемент реакции шарнирно-подвижной опоры – ее мо­дуль.

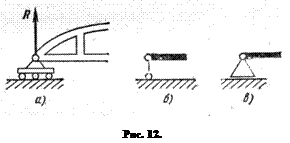По ГОСТу 2.770-68 шарнирно-подвижная опора для стержня изображается так, как показано на рис. 12, в.

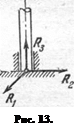4. Подпятник. Подпятник (рис. 13) представляет собой
соединение цилиндрического шарнира с опорной плоскостью. Такая связь позволяет вращаться валу (цилиндру) вокруг его оси и перемещаться вдоль нее, но только в одном направлении.

Реакция подпятника складывается из реакции цилиндрического подшипника, лежащей в плоскости, перпендикулярной к его оси (в общем случае она может быть разложена на составляющие R₁ и R₂ (рис. 13)), и нормальной реакции R₃ опорной плоскости.

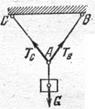5. Гибкая связь. Пусть груз весом G подвешен в точке А
на нитях так, как показано на рис. 14.

Если считать нити нерастяжимыми, то они не дают точке А удаляться от точки С по направлению нити СА и от точки В по направлению нити ВА. Следовательно, реакции ¹) Т_C и Т_S нерастяжимых гибких нитей всегда направлены вдоль нитей к точке их подвеса.

Гибкой связью, очевидно, может служить не только нить, но и трос, цепь и др. Рис.14

¹) Реакции гибких связей принято обозначать буквой Т.

6. Невесомый стержень. Нити на рис. 14 могут быть без изменения направлений реакций заменены твердыми стержнями, если пренебречь их весом и считать стержни соединенными по­средством идеальных шарниров. При отсутствии трения в идеальных шар­нирах приложенные к концам стержней силы всегда окажутся направленными вдоль этих стержней. Эти силы могут только растягивать или сжимать стерж­ни. В самом деле, как мы знаем, идеальный шарнир характеризуется только одной, нормальной к оси шарнира, реакцией. Но две силы, приложенные к стержню в его концах, могут уравновешиваться только тогда, когда они равны по модулю и направлены по одной прямой в проти­воположные стороны. Следовательно, реакция невесомого и шарнирно закрепленного стержня направлена вдоль линии, соединяющей центры шарниров.

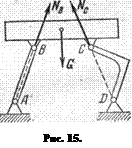Подобным же образом, оче­видно, направлены и реакции шарнирно закрепленных стерж­ней, подпирающих тело (рис. 15). Алгебраическое значение си­лы, действующей вдоль стержня и растягивающей или сжимаю­щей его, называется усилием в стержне; при растяжении уси­лие обычно считается положи­тельным, а при сжатии – отри­цательным ²).

В последующем изложении мы рассмотрим сначала сложение, разложение и равновесие сил в тех случаях, когда линии действия этих сил лежат в одной плоскости, а затем уже в тех случаях, когда они не лежат в одной плоскости. Изучение плоской системы мы начнем с так называемой системы сходящихся сил.

^а) Реакции стержней часто обозначают буквой N,