I.  , С - постоянная. II.
, С - постоянная. II.  .
.
III.  . IV.
. IV.  .
.
V. 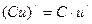 , С – постоянная. V.
, С – постоянная. V.  .
.
VII. 
Формулы дифференцирования
| Основные элементарные функции | Сложные функции |

| 
|

| 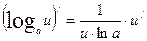
|

| 
|

| 
|
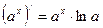
| 
|

| 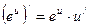
|

| 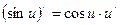
|

| 
|

| 
|

| 
|

| 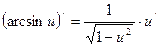
|

| 
|
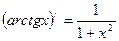
| 
|

| 
|
Примеры вычисления производных:
Пример 1.
 ;
; 
Решение:

Пример 2.
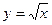 ;
; 
Решение:

Пример 3.
 ;
; 
Решение:
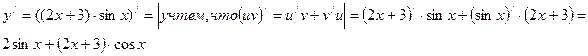
Пример 4.
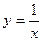 ;
; 
Решение:

Пример 5.
 . . 
|
Решение:
Для нахождения производной данной функции используем правила дифференцирования и таблицу производных. Так как производная суммы/разности равна сумме/разности производных, то
 постоянный множитель можно вынести за знак производной
постоянный множитель можно вынести за знак производной
 Воспользуемся формулой для производной степенной функции:
Воспользуемся формулой для производной степенной функции:

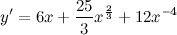

|
Пример 6.
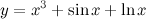 . . 
|
Решение:
Производная суммы равна сумме производных
 Воспользуемся формулами из таблицы производных - формулы производных степенной, тригонометрической и логарифмической функций:
Воспользуемся формулами из таблицы производных - формулы производных степенной, тригонометрической и логарифмической функций:


|
Пример 7.
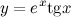 . .  Решение:
Решение:
|
По свойству дифференцирования произведения
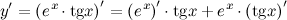 теперь воспользуемся формулами из таблицы производных - формулами для производных показательной и тригонометрической функций:
теперь воспользуемся формулами из таблицы производных - формулами для производных показательной и тригонометрической функций:


|
Найти производную функции 
|
Воспользуемся правилом дифференцирования частного:
 Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем:
Производная суммы/разности равна сумме/разности производных и константу можно выносить за знак производной, поэтому имеем:


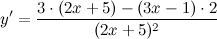


|
Пример 8.
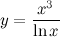 . . 
|
Решение:
По свойству дифференцирования частного получаем:
 Далее пользуясь формулами для производных логарифмической и степенной функции, получим:
Далее пользуясь формулами для производных логарифмической и степенной функции, получим:


 Для вычисления производной функции использовались правила дифференцирования и таблица производных функций.
Для вычисления производной функции использовались правила дифференцирования и таблица производных функций.
|
Пример 9.
 . .  Решение:
Решение:
|
По свойству дифференцирования сложной функции вначале находим производную натурального логарифма и домножаем на производную подлогарифмической функции:
 Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем:
Производная суммы равна сумме производных и константу можно выносить за знак производной, поэтому имеем:

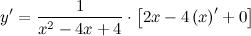

 Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки:
Знаменатель дроби можно свернуть по формуле квадрат разности, а в числителе двойку вынесем как общий множитель за скобки:
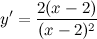 сокращаем:
сокращаем:

|
Пример 10.
 . .  .
Решение: .
Решение:
|
По свойству дифференцирования сложной функции производная от данной функции сначала берется как от арксинуса, а затем умножается на производную от корня:
 Производная
Производная  так же берется по правилам дифференцирования сложной функции, сначала производная от корня, а затем умножается на производную от подкоренного выражения: так же берется по правилам дифференцирования сложной функции, сначала производная от корня, а затем умножается на производную от подкоренного выражения:
 производная разности равна разности производных, тогда
производная разности равна разности производных, тогда




|
Задания
|
|
|
Вычислить производные, используя правила и формулы дифференцирования:
1)  6)
6)  11)
11) 
2)  7)
7)  12)
12) 
3)  8)
8)  13)
13) 
|
|
|
4) 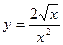 9)
9)  14)
14) 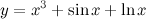
5) 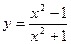 10)
10)  15)
15) 
 2015-10-22
2015-10-22 655
655








