Приклад 1. Три однакові точкові заряди по 1 нКл кожен розміщені у вершинах рівностороннього трикутника. Який негативний заряд потрібно помістити в центрі трикутника, щоб зазначена система зарядів знаходилася у рівновазі?
Дано: q 1 = q 2 = q 3 = 10-9 Кл;  =
=  =
=  = 600.
= 600.
Знайти: q 4.
Розв’язок. Оскільки всі три заряди у вершинах трикутника знаходяться в однакових умовах, досить з’ясувати, який заряд потрібно помістити в центр трикутника, щоб який-небудь один із трьох зарядів знаходився в рівновазі. Заряд q 1 буде знаходитись в рівновазі, якщо векторна сума діючих на нього сил дорівнює нулю (рис. 3.1)
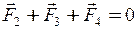 , (1) де , (1) де  , ,  і і 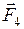 – сили, з якими діють на обраний заряд q 1 відповідно заряди q 2, q 3 і q 4. Введемо допоміжну силу – сили, з якими діють на обраний заряд q 1 відповідно заряди q 2, q 3 і q 4. Введемо допоміжну силу 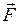 , що є рівнодіючою сил , що є рівнодіючою сил  і і  , і спрямована уздовж прямої, що з’єднує центр трикутника з даним зарядом , і спрямована уздовж прямої, що з’єднує центр трикутника з даним зарядом  . (2) . (2) | 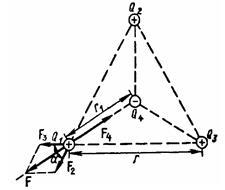 Рис. 3.1. Рис. 3.1. |
Сили 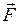 і
і 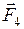 спрямовані уздовж однієї прямої, але в протилежні боки, тому, з урахуванням виразу (2), можна перейти до скалярної форми рівняння (1)
спрямовані уздовж однієї прямої, але в протилежні боки, тому, з урахуванням виразу (2), можна перейти до скалярної форми рівняння (1)
 або
або  . (3)
. (3)
Із симетрії задачі випливає, що сили F 2 і F 3 однакові за величиною. Тому, застосовуючи закон Кулона для величин, що входять у (3), легко одержати (рис. 3.1)
 ; (4 а)
; (4 а)
 , (4 б)
, (4 б)
де відстань r 1 можна знайти з геометрії трикутника
 . (5)
. (5)
Підставляючи вираз (4) у (3), одержимо
 . (6)
. (6)
Звідси, використовуючи (5), можна одержати остаточно
 . (7)
. (7)
Обчислення.
 = 5,77·10-9 Кл.
= 5,77·10-9 Кл.
Відповідь: q 4 = 5,77·10-9 Кл.
Приклад 2. Два точкові електричні заряди 1 нКл і –2 нКл знаходяться у повітрі на відстані 10 см один від одного. Визначити напруженість і потенціал електричного поля, створюваного цими зарядами, у точці, віддаленій від першого заряду на 9 см і від другого – на 7 см.
Дано: q 1= 10-9 Кл; q 2= –2·10-9 Кл; d = 0,1 м; r 1= 9·10-2 м; r 2= 7·10-2 м.
Знайти: E;  .
.
Розв’язок. Відповідно до принципу суперпозиції, напруженість електричного поля 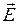 в пошукуваній точці дорівнює векторній сумі полів
в пошукуваній точці дорівнює векторній сумі полів  і
і  , створених кожним зарядом q 1 і q 2 окремо
, створених кожним зарядом q 1 і q 2 окремо
 , (1)
, (1)
де
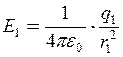 ; (2 а)
; (2 а)
 . (2 б)
. (2 б)
Вектор  (рис. 3.2) спрямований уздовж силової лінії від заряду
(рис. 3.2) спрямований уздовж силової лінії від заряду
q 1, оскільки цей заряд позитивний; вектор  спрямований за силовою лінії до заряду q 2, тому що цей заряд негативний. Модуль результуючого вектора спрямований за силовою лінії до заряду q 2, тому що цей заряд негативний. Модуль результуючого вектора  знайдемо за теоремою косинусів знайдемо за теоремою косинусів  . (3) . (3) |  Рис. 3.2. Рис. 3.2. |
Тут  – кут між векторами
– кут між векторами  і
і  , що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r 1 і r 2
, що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r 1 і r 2
 . (4)
. (4)
Підставляючи в (3) вираз (2) і (4), одержимо
 . (5)
. (5)
Потенціал результуючого поля, відповідно до принципу суперпозиції, дорівнює алгебраїчній сумі потенціалів
 . (6)
. (6)
Тут 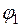 і
і  – потенціали полів точкових зарядів q 1 і q 2 у пошукуваній точці
– потенціали полів точкових зарядів q 1 і q 2 у пошукуваній точці
 ; (7 а)
; (7 а)
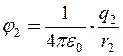 . (7 б)
. (7 б)
Таким чином, з (6) і (7) одержимо
 , (8)
, (8)
де варто враховувати знаки зарядів q 1 і q 2.
При обчисленнях візьмемо до уваги, що в одиницях СІ загальний множник виразів (5) і (8) дорівнює
 = 9·109 м/Ф.
= 9·109 м/Ф.
Обчислення.
 = 3,58·103 В/м;
= 3,58·103 В/м;
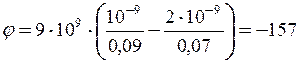 В.
В.
Відповідь: E = 3,58·103 В/м;  В.
В.
Приклад 3. Уздовж тонкого кільця рівномірно розподілений заряд у 40 нКл з лінійною густиною 50 нКл/м. Визначити напруженість електричного поля, створеного цим зарядом у точці, що лежить на осі кільця і віддалена від його центра на відстань, що дорівнює половині радіуса.
Дано: q = 4·10-8 Кл;  = 5·10-8 Кл/м; h = R /2.
= 5·10-8 Кл/м; h = R /2.
Знайти: E.
Розв’язок. Виділимо на кільці малу ділянку довжиною dl (рис. 3.3). Оскільки заряд dq 1 =  dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля 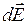 , що створено цим зарядом, можна записати у вид , що створено цим зарядом, можна записати у вид  . (1) . (1) | 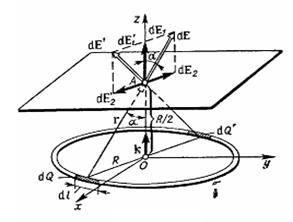 Рис. 3.3. Рис. 3.3. |
Розкладемо вектор 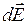 на дві складові:
на дві складові: 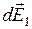 , перпендикулярну площини кільця, і
, перпендикулярну площини кільця, і  , паралельну до площини кільця, тобто
, паралельну до площини кільця, тобто
 . (2)
. (2)
Напруженість E електричного поля в пошукуваній точці знайдемо інтегруванням
 ,
,
де інтегрування ведеться по всіх елементах зарядженого кільця. З рисунка бачимо, що для кожної пари зарядів dq і dq ′, розташованих симетрично щодо центра кільця, складові  і
і  однакові за модулем і протилежні за напрямком:
однакові за модулем і протилежні за напрямком:  . Тому векторна сума
. Тому векторна сума  . Складові
. Складові 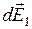 для всіх елементів кільця напрямлені уздовж осі кільця, тому
для всіх елементів кільця напрямлені уздовж осі кільця, тому
 , (3)
, (3)
де 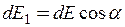 , або з урахуванням (1)
, або з урахуванням (1)  ,
,  ,
,  .
.
З урахуванням цього
 . (4)
. (4)
Із співвідношення  визначимо радіус кільця
визначимо радіус кільця  . Тоді
. Тоді
 . (5)
. (5)
Зробимо обчислення.
 = 7,92·103 В/м.
= 7,92·103 В/м.
Відповідь: E = 7,92·103 В/м.
Приклад 4. Нескінченна площина, розташована вертикально, заряджена рівномірно з поверхневою густиною заряду 40 мкКл/м2. На шовковій нитці, один з кінців якої закріплений у точці на цій площині, підвішена кулька масою 1 г, що несе заряд 1 нКл. Який кут із площиною утворить нитка, на якій висить кулька?
Дано:  = 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
= 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
Знайти:  .
.
Розв’язок. У стані рівноваги результуюча усіх сил, що діють на кульку (рис. 3.4), дорівнює нулю
 . (1)
. (1)
Тут  , ,  і і 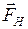 – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки. Векторна сума взаємно перпендикулярних сил – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки. Векторна сума взаємно перпендикулярних сил  і і  (на рис. 3.4 – сила (на рис. 3.4 – сила 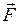 ) спрямована уздовж нитки і в стані рівноваги урівноважується силою ) спрямована уздовж нитки і в стані рівноваги урівноважується силою 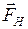 . З цього випливає, що пошукуваний кут дорівнює кутові між векторами . З цього випливає, що пошукуваний кут дорівнює кутові між векторами  і і 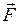 , тому , тому |  Рис. 3.4. Рис. 3.4. |
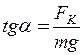 . (2)
. (2)
Кулонівська сила, що діє на заряджену кульку в однорідному електричному полі площини, дорівнює
 . (3)
. (3)
Тут E – напруженість електричного поля, створювана рівномірно зарядженою площиною
 . (4)
. (4)
Таким чином, з (2)–(4) можна одержати остаточний вираз для пошукуваного кута
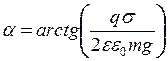 . (5)
. (5)
Обчислення.
 = 130.
= 130.
Відповідь:  = 130.
= 130.
Приклад 5. Електричне поле створене довгим циліндром радіусом 1 см, рівномірно зарядженим з лінійною густиною 20 нКл/м. Визначити швидкість, яку одержить електрон під дією поля, наблизившись до циліндра з відстані 2 см до відстані 0,5 см від поверхні циліндра.
Дано: R = 10-2 м;  = 2·10-8 Кл/м; a 1 = 2·10-2 м; a 2 = 5·10-3 м;
= 2·10-8 Кл/м; a 1 = 2·10-2 м; a 2 = 5·10-3 м; 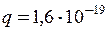 Кл; m = 9,1·10-31 кг;
Кл; m = 9,1·10-31 кг;  = 0.
= 0.
Знайти:  .
.
Розв’язок. Електрон рухається під дією електростатичного поля, створеного зарядженим циліндром. У довільній точці на відстані r від осі циліндра ( ) напруженість E його електростатичного поля визначається формулою
) напруженість E його електростатичного поля визначається формулою
 . (1)
. (1)
Робота переміщення електрона в електростатичному полі дорівнює добуткові заряду на різницю потенціалів
 . (2)
. (2)
Тут 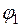 і
і  – потенціал електростатичного поля циліндра відповідно у точках, що знаходяться на відстані r 1 і r 2 від осі, де
– потенціал електростатичного поля циліндра відповідно у точках, що знаходяться на відстані r 1 і r 2 від осі, де
 ; (3 а)
; (3 а)
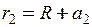 . (3 б)
. (3 б)
Ця робота витрачається на зміну кінетичної енергії електрона, отже
 , (3)
, (3)
де  .
.
Для визначення різниці потенціалів скористаємось співвідношенням між напруженістю поля і зміною потенціалу
 . (4)
. (4)
Підставивши в це рівняння вираз для напруженості поля, створюваного нескінченно довгим циліндром, одержимо
 . (5)
. (5)
Остаточно, підставляючи (4) у (3), можна одержати пошукувану розрахункову формулу
 . (5)
. (5)
Обчислення.
 м/с.
м/с.
Відповідь: 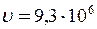 м/с.
м/с.
Приклад 6. На плаский повітряний конденсатор подається різниця потенціалів 2 кВ. Розміри пластин 40х60 см2, відстань між ними
0,5 см. Після зарядки конденсатор відключають від джерела і потім розсувають пластини так, що відстань між ними збільшується вдвічі. Визначити: роботу з розсування пластин; густину енергії електричного поля до і після розсування обкладок.
Дано: U 1 = 2·103 В; S = 0,24 м2; d 1 = 5·10-3 м; d 2 = 2 d 1;  = 1.
= 1.
Знайти: A, w 1, w 2.
Розв’язок. Робота з розсування пластин дорівнює зміні енергії зарядженого конденсатора
A = W 2 – W 1. (1)
Енергія конденсатора визначається формулами
 ;
;  , (2)
, (2)
де C 1 і C 2 – ємність конденсатора до і після розсування обкладок
 ;
;  . (3)
. (3)
Вважаючи на те, що конденсатор було відключено від джерела, заряд q на його обкладках не змінився, тобто
q = C 1 U 1 = C 2 U 2. (4)
Підставляючи вираз (3) у (4), легко одержати:
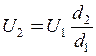 . (5)
. (5)
Підставивши (2), (3) і (5) у (1), знайдемо:
 . (6)
. (6)
Об’ємну густину енергії електричного поля в конденсаторі можна знайти, розділивши його енергію на об’єм
 ; (7 а)
; (7 а)
 . (7 б)
. (7 б)
У даній задачі зв’язок між напругами конденсатора в двох станах виражається формулою (5). Підставляючи її в (7 б) одержимо
 . (8)
. (8)
Обчислення.
 = 8,45·10-4 Дж;
= 8,45·10-4 Дж;
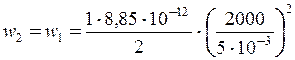 = 0,7 Дж·м-3.
= 0,7 Дж·м-3.
Відповідь: А = 8,45·10-4 Дж; w 2 = w 1 = 0,7 Дж·м-3.
Приклад 7. Конденсатор ємністю 3 мкФ було заряджено до різниці потенціалів 40 В. Після відключення від джерела струму конденсатор з’єднали паралельно з іншим незарядженим конденсатором об’ємом 5 мкФ. Яка енергія була витрачена на утворення іскри у момент приєднання другого конденсатора?
Дано: C 1 = 3·10-6 Ф; C 2 = 5·10-6 Ф; U 1 = 40 В; U 2 = 0 В.
Знайти:  .
.
Розв’язок. Енергія, витрачена на утворення іскри
 , (1)
, (1)
де  – енергія конденсатора;
– енергія конденсатора;  – енергія батареї паралельно з’єднаних конденсаторів.
– енергія батареї паралельно з’єднаних конденсаторів.
З огляду на те, що заряд після приєднання другого конденсатора залишився попереднім, виразимо різницю потенціалів U 2 у такий спосіб
 . (2)
. (2)
Підставивши вираз для U 2, знайдемо
 або
або  . (3
. (3
Обчислення.
 Дж = 1,5·10-3 Дж.
Дж = 1,5·10-3 Дж.
Відповідь: 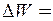 1,5·10-3 Дж.
1,5·10-3 Дж.
Приклад 8. Батарея складається з п’яти однакових гальванічних елементів, з’єднаних послідовно. Кожен з цих елементів має ЕРС 1,4 В и внутрішній опір 0,3 Ом. При якому струмі корисна потужність батареї буде дорівнювати 8 Вт? Яку найбільшу корисну потужність може віддавати ця батарея?
Дано:  = 1,4 В; r = 0,3 Ом; n =5; PR = 8 Вт.
= 1,4 В; r = 0,3 Ом; n =5; PR = 8 Вт.
Знайти: I; PR,max.
Розв’язок. При послідовному з’єднанні декількох гальванічних елементів їх можна замінити в розрахунках одним еквівалентним елементом. Внутрішній опір цього еквівалентного елемента дорівнює сумі внутрішніх опорів тих елементів, з яких він складений, а його ЕРС дорівнює алгебраїчній сумі ЕРС елементів. Це дозволяє записати закон Ома для даної задачі у такому вигляді
 . (1)
. (1)
Корисна потужність, тобто потужність, що виділяється у навантаженні з опором R, дорівнює
 . (2)
. (2)
Якщо тепер виразити опір R з рівняння (2) і підставити результат у вираз (1), після нескладних перетворень можна одержати таке квадратне (по струму I) рівняння
 . (3)
. (3)
Рішення цього рівняння має стандартний вигляд
 . (4)
. (4)
Щоб знайти найбільшу корисну потужність, що віддається цією батареєю в зовнішнє коло, спочатку запишемо потужність як функцію опору навантаження, для чого підставимо вираз (1) у (2)
 . (5)
. (5)
Тепер скористаємося умовою екстремуму (максимуму) цієї функції, для чого знайдемо похідну від виразу (5) від змінної R, і дорівняємо її нуля
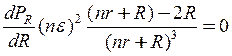 . (6)
. (6)
З розв’язку цього рівняння випливає
 . (7)
. (7)
Підставляючи це рішення у вираз (5), одержимо остаточну формулу для обчислення максимальної потужності, що віддається даною батареєю в навантаження
 . (8)
. (8)
Обчислення.
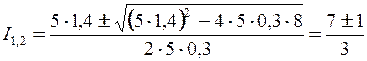 ,
,
звідки
I 1 = 2,66 A; I 2 = 2,0 A;  = 8,16 Вт.
= 8,16 Вт.
Відповідь: I 1 = 2,66 A; I 2 = 2,0 A; P R,max = 8,16 Вт.
Приклад 9. З яким коефіцієнтом корисної дії працює акумулятор, ЕРС якого 2,15 В, якщо у зовнішньому колі опором 0,25 Ом тече струм 5 А?
Дано:  = 2,15 В; R = 0,25 Ом; I = 5 А.
= 2,15 В; R = 0,25 Ом; I = 5 А.
Знайти:  .
.
Розв’язок. Корисна потужність PR, що виділяється у навантаженні опором R, може бути визначена з виразом
 . (1)
. (1)
Повну потужність P Σ, що віддається акумулятором, знайдемо з виразу
P Σ = I  . (2)
. (2)
Коефіцієнт корисної дії, мабуть, дорівнює відношенню корисної потужності до повної. Таким чином, з (1) і (2) легко одержати остаточну розрахункову формулу
 . (3)
. (3)
Обчислення.
 = 0,58.
= 0,58.
Відповідь:  = 58 %.
= 58 %.
Приклад 10. У провіднику опором 20 Ом сила струму зростає за лінійним законом від нуля до 6 А за 2 с. Визначити кількість теплоти, що виділяється в цьому провіднику за першу секунду і за другу секунду. У скільки разів теплота, виділена за другу секунду, більша від теплоти, виділеної за першу секунду?
Дано: R = 20 Ом; t 0 = 0; t k = 2 c; I 0 = 0; I = 6 А; 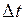 = 2 c.
= 2 c.
Знайти: Q 1, Q 2, Q 2, Q 1.
Розв’язок. Закон Джоуля-Ленца у виді  справедливий для постійного струму. Якщо сила струму в провіднику змінюється, то цей закон справедливий для нескінченно малого інтервалу часу і записується так
справедливий для постійного струму. Якщо сила струму в провіднику змінюється, то цей закон справедливий для нескінченно малого інтервалу часу і записується так
 . (1)
. (1)
Тут сила струму I є деякою функцією часу 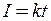 , де k – коефіцієнт пропорційності, що характеризує швидкість зміни сили струму
, де k – коефіцієнт пропорційності, що характеризує швидкість зміни сили струму
 А/с = 3 А/с. (2)
А/с = 3 А/с. (2)
Тоді  .
.
Для визначення теплоти, що виділяється за час Δ t, проінтегруємо цей вираз
 . (3)
. (3)
Тоді
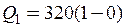 Дж = 60 Дж;
Дж = 60 Дж;
 Дж = 420 Дж.
Дж = 420 Дж.
Отже,  , тобто за другу секунду виділяється теплоти в 7 разів більше, ніж за першу.
, тобто за другу секунду виділяється теплоти в 7 разів більше, ніж за першу.
Відповідь: Q 1 = 60 Дж; Q 2 = 420 Дж; n = 7.
Приклад 11. Визначити силу струму в усіх ділянках кола, вказаного на рис. 3.5, і що включають ЕРС ( = =  = 3 В, = 3 В,  = 1 В), а також провідники, що мають опори R 1 = 5 Ом, R 2 = 3 Ом, R 3 = 1 Ом. = 1 В), а також провідники, що мають опори R 1 = 5 Ом, R 2 = 3 Ом, R 3 = 1 Ом. |  Рис. 3.5. Рис. 3.5. |
Дано:  =
=  = 3 В;
= 3 В;  = 1 В; R 1 = 5 Ом; R 2 = 3 Ом; R 3 = 1 Ом.
= 1 В; R 1 = 5 Ом; R 2 = 3 Ом; R 3 = 1 Ом.
Знайти: I 1, I 2, I 3.
Розв’язок. Для розв’язку задачі використовуються закони Кірхгофа. Якщо напрямок струмів вибрати так, як показано на рис. 3.5, то за першим законом Кірхгофа для вузла а одержимо
I 2 – I 1 – I 3 = 0. (1)
За другим законом Кірхгофа для контуру ( ,
,  , R 2 і R 3), лівого на схемі, можна записати рівняння
, R 2 і R 3), лівого на схемі, можна записати рівняння
 . (2)
. (2)
Для іншого контуру (e 1, R 1 і R 3), правого на схемі, маємо аналогічне рівняння
 . (3)
. (3)
Отримані рівняння являють собою систему трьох рівнянь із трьома невідомими, котру нескладно розв’язати. Зокрема, із другого рівняння можна вивести струм I 2 через струм I 3 і відомі величини, а з третього – струм I 1 через струм I 3 і відомі величини
 ; (4 а)
; (4 а)
 . (4 б)
. (4 б)
Після підстановки цих виразів у перше рівняння легко одержати остаточну формулу для струму I 3
 . (4 в)
. (4 в)
Зробимо обчислення.
 = 0,826 А.
= 0,826 А.
Підставляючи отриманий результат у формули для I 1 і I 2, одержимо
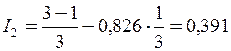 А;
А;
 А.
А.
Для перевірки отримані результати підставимо у вихідне рівняння, записане за першим законом Кірхгофа
0,391 – (–0,435) – 0,826 = 0.
Таким чином, ми переконалися, що задача розв’язана вірно. Для I 1 отримано негативне значення. Це означає, що в дійсності напрямок даного струму виявився протилежним до того, який було обрано нами довільно (див. рис. 3.5).
Відповідь: I 1 = –0,435 А; I 2 = 0,391 А; I 3 = 0,826 А.
 2015-10-22
2015-10-22 7998
7998
