Варианты контрольных заданий
В табл. 1 приведены варианты задач, входящих в контрольную работу № 11 “Специальные главы высшей математики”. Студент должен выполнять контрольную работу по варианту, номер которого совпадает с последней цифрой номера его зачетной книжки. Первая цифра номера задачи соответствует номеру контрольной работы, а последняя - номеру варианта.
Таблица 1
Контрольная работа № 11
| Вариант | Задача | |||||
| 11.1 | 11.11 | 11.21 | 11.31 | 11.41 | 11.51 | |
| 11.2 | 11.12 | 11.22 | 11.32 | 11.42 | 11.52 | |
| 11.3 | 11.13 | 11.23 | 11.33 | 11.43 | 11.53 | |
| 11.4 | 11.14 | 11.24 | 11.34 | 11.44 | 11.54 | |
| 11.5 | 11.15 | 11.25 | 11.35 | 11.45 | 11.55 | |
| 11.6 | 11.16 | 11.26 | 11.36 | 11.46 | 11.56 | |
| 11.7 | 11.17 | 11.27 | 11.37 | 11.47 | 11.57 | |
| 11.8 | 11.18 | 11.28 | 11.38 | 11.48 | 11.58 | |
| 11.9 | 11.19 | 11.29 | 11.39 | 11.49 | 11.59 | |
| 11.10 | 11.20 | 11.30 | 11.40 | 11.50 | 11.60 |
Условия заданий для контрольной работы
Специальные главы высшей математики (к. р. №11)
11.1–11.10. Представить заданную функцию 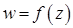 , где
, где 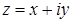 в виде
в виде 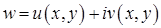 . Проверить ее на дифференцируемость и аналитичность. Найти производную, если она существует.
. Проверить ее на дифференцируемость и аналитичность. Найти производную, если она существует.
11.1. 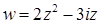 .
.
11.2. 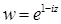 .
.
11.3. 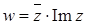 .
.
11.4. 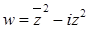 .
.
11.5. 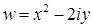 .
.
11.6. 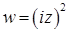 .
.
11.7. 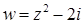 .
.
11.8. 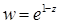 .
.
11.9. 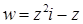 .
.
11.10. 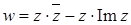 .
.
11.11–11.20. Вычислить интеграл, используя интегральную формулу Коши или теорему Коши. Изобразить контуры интегрирования.
11.11. 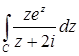 , где
, где 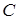 : 1)
: 1) 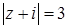 ; 2)
; 2) 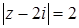 .
.
11.12. 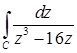 где
где 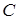 : 1)
: 1) 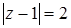 ; 2)
; 2) 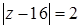 .
.
11.13. 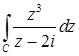 , где
, где 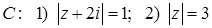 .
.
11.14. 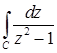 , где
, где 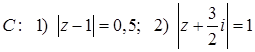 .
.
11.15. 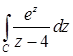 , где
, где 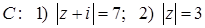 .
.
11.16. 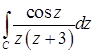 , где
, где 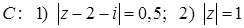 .
.
11.17. 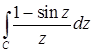 , где
, где 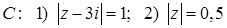 .
.
11.18. 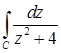 , где
, где 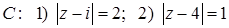 .
.
11.19. 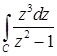 , где
, где 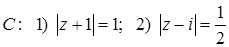 .
.
11.20. 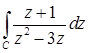 , где
, где 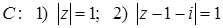 .
.
11.21–11.30. Данную функцию 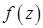 разложить в ряд Лорана в окрестности точки
разложить в ряд Лорана в окрестности точки 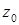 . Определить характер особой точки. Найти вычет функции в точке
. Определить характер особой точки. Найти вычет функции в точке 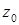 .
.
11.21. 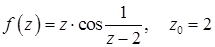 .
.
11.22. 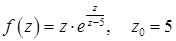 .
.
11.23. 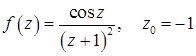 .
.
11.24. 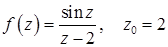 .
.
11.25. 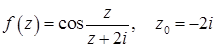 .
.
11.26. 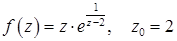 .
.
11.27. 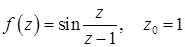 .
.
11.28. 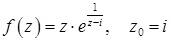 .
.
11.29. 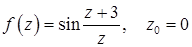 .
.
11.30. 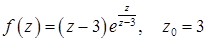 .
.
11.31–11.40. Методами операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
11.31. 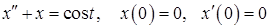 .
.
11.32. 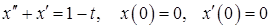 .
.
11.33. 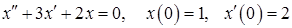 .
.
11.34. 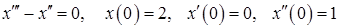 .
.
11.35. 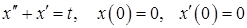 .
.
11.36. 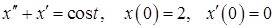 .
.
11.37. 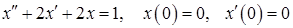 .
.
11.38. 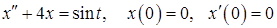 .
.
11.39. 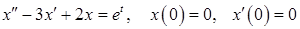 .
.
11.40. 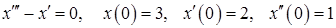
11.41–11.50. Методами операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
11.41. 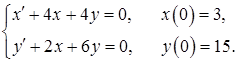
11.42. 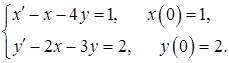
11.43. 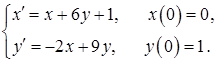
11.44. 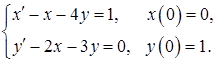
11.45. 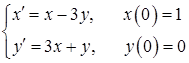
11.46. 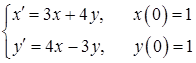
11.47. 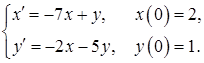
11.48. 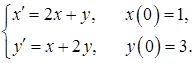
11.49. 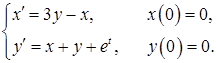
11.50. 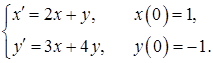
11.51–11.60. Дан тонкий однородный стержень 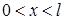 , боковая поверхность которого теплоизолирована. Найти распределение температуры
, боковая поверхность которого теплоизолирована. Найти распределение температуры 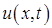 в стержне, если задана его начальная температура
в стержне, если задана его начальная температура 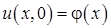 и дополнительные краевые условия.
и дополнительные краевые условия.
11.51. Правый конец стержня теплоизолирован, левый конец поддерживается при постоянной температуре 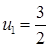 ,
, 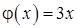 .
.
11.52. Концы стержня поддерживаются при постоянной температуре равной нулю, 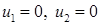 ,
, 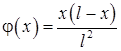 .
.
11.53. Правый конец стержня теплоизолирован, левый конец поддерживается при постоянной температуре 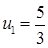 ,
, 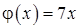 .
.
11.54. Концы стержня поддерживаются при постоянной температуре равной нулю, 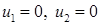 ,
, 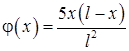 .
.
11.55. Левый конец стержня теплоизолирован, правый конец поддерживается при постоянной температуре 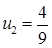 ,
, 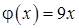 .
.
11.56. Концы стержня поддерживаются при постоянной температуре равной нулю, 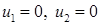 ,
, 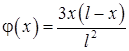 .
.
11.57. Левый конец стержня теплоизолирован, правый стержня поддерживается при постоянной температуре 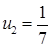 ,
, 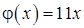 .
.
11.58. Концы стержня поддерживаются при постоянной температуре равной нулю, 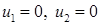 ,
, 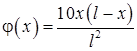 .
.
11.59. Правый конец стержня теплоизолирован, левый стержня поддерживается при постоянной температуре 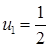 ,
, 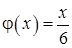 .
.
11.60. Левый конец стержня теплоизолирован, правый стержня поддерживается при постоянной температуре 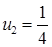 ,
, 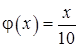 .
.
 2015-10-22
2015-10-22 599
599







