(только для студентов заочной формы, со сроком обучения 5 лет)
Вариант 1
1. Вычислить матрицу 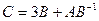 , где
, где 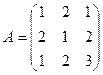 и
и 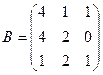 .
.
2. Даны матрицы:
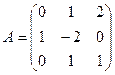 и
и 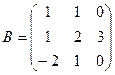 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. По координатам вершин пирамиды 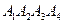 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 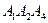 .
.
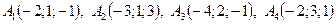 .
.
5. Привести уравнение кривой второго порядка 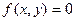 к каноническому виду и найти точки пересечения её с прямой
к каноническому виду и найти точки пересечения её с прямой  . Построить в одной системе координат графики кривой и прямой.
. Построить в одной системе координат графики кривой и прямой.
 .
.
6. Построить графики функций: 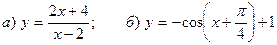 .
.
7. Вычислить пределы функций:
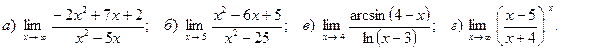
Вариант 2
1. Вычислить матрицу 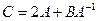 , где
, где 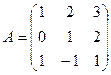 и
и 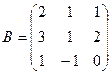 .
.
2. Даны матрицы:
 и
и 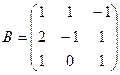 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
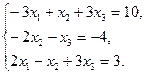
4. По координатам вершин пирамиды 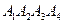 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 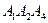 .
.
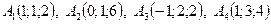 .
.
5. Привести уравнение кривой второго порядка 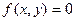 к каноническому виду и найти точки пересечения её с прямой
к каноническому виду и найти точки пересечения её с прямой  . Построить в одной системе координат графики кривой и прямой.
. Построить в одной системе координат графики кривой и прямой.
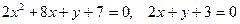 .
.
6. Построить графики функций: 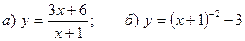 .
.
7. Вычислить пределы функций:
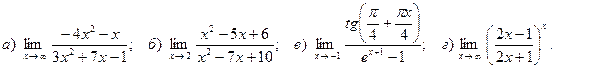
Вариант 3
1. Вычислить матрицу  , где
, где 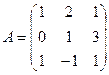 и
и 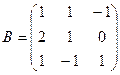 .
.
2. Даны матрицы:
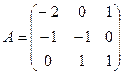 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
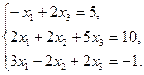
4. По координатам вершин пирамиды 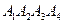 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 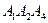 .
.
 .
.
5. Привести уравнение кривой второго порядка 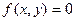 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
 .
.
6. Построить графики функций: 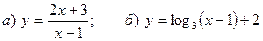 .
.
7. Вычислить пределы функций:
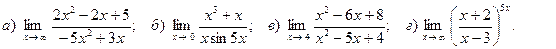
Вариант 4
1. Вычислить матрицу  , где
, где 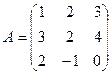 и
и 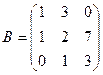 .
.
2. Даны матрицы:
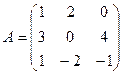 и
и 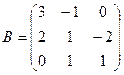 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
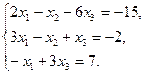
4. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
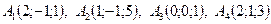 .
.
5. Привести уравнение кривой второго порядка 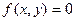 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
 .
.
6. Построить графики функций:  .
.
7. Вычислить пределы функций:

Вариант 5
1. Вычислить матрицу  , где
, где 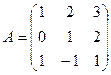 и
и 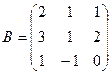 .
.
2. Даны матрицы:
 и
и 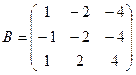 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
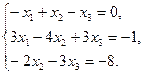
4. По координатам вершин пирамиды 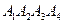 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 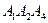 .
.
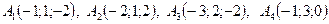 .
.
5. Привести уравнение кривой второго порядка 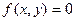 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
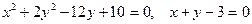 .
.
6. Построить графики функций: 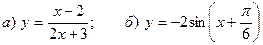 .
.
7. Вычислить пределы функций:
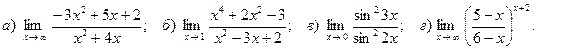
Вариант 6
1. Вычислить матрицу 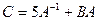 , где
, где 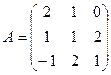 и
и 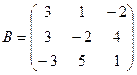 .
.
2. Даны матрицы:
 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. По координатам вершин пирамиды 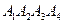 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 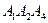 .
.
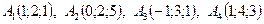 .
.
5. Привести уравнение кривой второго порядка 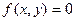 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
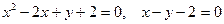 .
.
6. Построить графики функций: 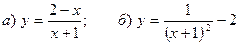 .
.
7. Вычислить пределы функций:
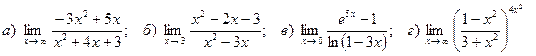
Вариант 7
1. Вычислить матрицу 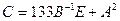 , где
, где 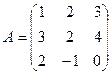 и
и 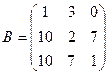 .
.
2. Даны матрицы:
 и
и 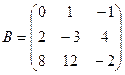 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
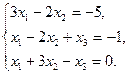
4. По координатам вершин пирамиды 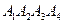 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 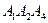 .
.
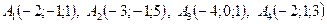 .
.
5. Привести уравнение кривой второго порядка 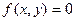 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
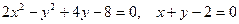 .
.
6. Построить графики функций:  .
.
7. Вычислить пределы функций:
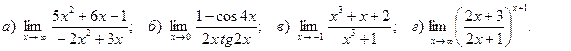
Вариант 8
1. Вычислить матрицу 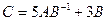 , где
, где 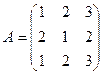 и
и 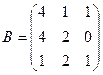 .
.
2. Даны матрицы:
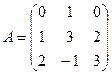 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. По координатам вершин пирамиды 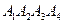 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 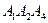 .
.
 .
.
5. Привести уравнение кривой второго порядка 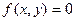 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
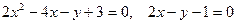 .
.
6. Построить графики функций:  .
.
7. Вычислить пределы функций:
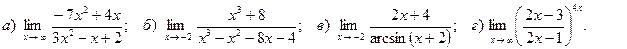
Вариант 9
1. Вычислить матрицу  , где
, где 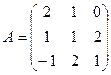 и
и 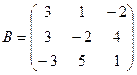 .
.
2. Даны матрицы:
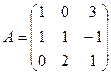 и
и  . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.
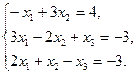
4. По координатам вершин пирамиды 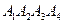 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 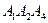 .
.
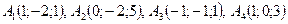 .
.
5. Привести уравнение кривой второго порядка 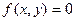 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
 .
.
6. Построить графики функций:  .
.
7. Вычислить пределы функций:

Вариант 10
1. Вычислить матрицу  , где
, где 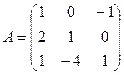 и
и 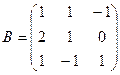 .
.
2. Даны матрицы:
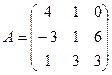 и
и 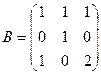 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. По координатам вершин пирамиды  найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и  .
.
 .
.
5. Привести уравнение кривой второго порядка 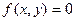 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
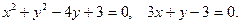
6. Построить графики функций: 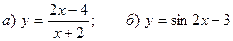 .
.
7. Вычислить пределы функций:
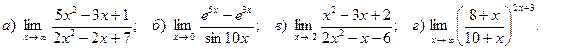
Демонстрационный вариант контрольной работы №1
1. Вычислить матрицу 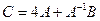 , где
, где  и
и 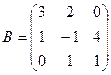 .
.
2. Даны матрицы:
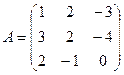 и
и 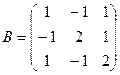 . Найти произведение
. Найти произведение  . Проверить на данном
. Проверить на данном
примере, что определитель произведения матриц равен произведению их определителей.
3. Найти решение системы линейных уравнений: 1) методом Гаусса, 2) методом Крамера, 3) методом обратной матрицы, для чего записать систему в матричной форме и решить ее средствами матричного исчисления, при этом правильность вычисления обратной матрицы проверить, используя матричное умножение.

4. По координатам вершин пирамиды 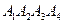 найти:
найти:
1) длины рёбер  и
и  ;
;
2) угол между рёбрами  и
и  ;
;
3) площадь грани  ;
;
4) объём пирамиды;
5) уравнение плоскостей  и
и 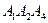 .
.
 .
.
5. Привести уравнение кривой второго порядка 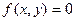 к каноническому виду и найти
к каноническому виду и найти
точки пересечения её с прямой  . Построить в одной системе координат
. Построить в одной системе координат
графики кривой и прямой.
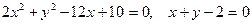 .
.
6. Построить графики функций: 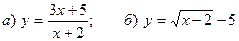 .
.
7. Вычислить пределы функций:
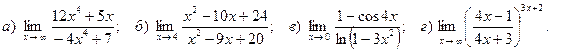
Решение демонстрационного варианта контрольной работы № 1
Решение задачи 1
1) вычислим  :
:
4  =
= 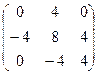
2) Найдём 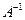 :
:
Найдём определитель матрицы  :
: 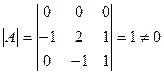 , следовательно, обратная матрица существует.
, следовательно, обратная матрица существует.
Найдём алгебраические дополнения ко всем элементам матрицы  .
.


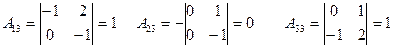
Составим матрицу из этих алгебраических дополнений 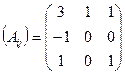 .
.
Запишем матрицу 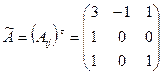 .
.  .
.
3) Вычислим произведение 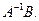
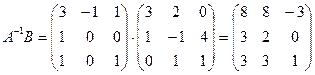 .
.
4)  .
.
Ответ:  .
.
Решение задачи 2
1) 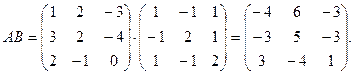
2) 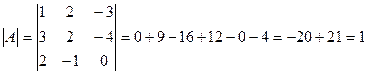
3) 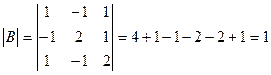
4) 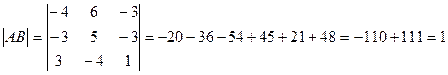
Из 2)-4) следует, что 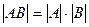 , т.к.
, т.к. 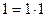 что и требовалось доказать.
что и требовалось доказать.
Ответ:  .
.
Решение задачи 3
1. Метод Крамера
Вычислим определитель системы: 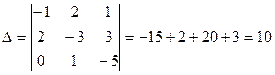 .
.
Найдём  :
:
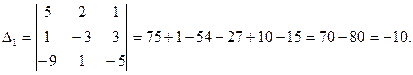

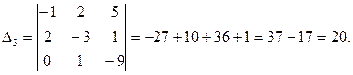
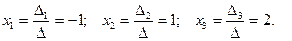
Проверка:
подставим полученные значения неизвестных в систему

Ответ:  .
.
2. Метод обратной матрицы
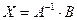 , где
, где 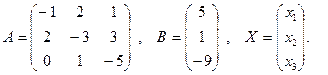
Так как определитель матрицы системы отличен от нуля: 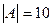 , то матрица
, то матрица  имеет обратную. Для нахождения обратной матрицы
имеет обратную. Для нахождения обратной матрицы 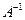 вычислим алгебраические дополнения элементов матрицы
вычислим алгебраические дополнения элементов матрицы  .
.

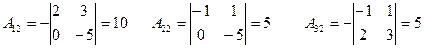
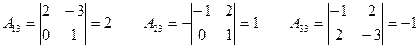
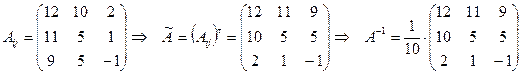
Матричное решение системы имеет вид
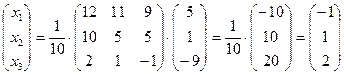
откуда следует (из условия равенства двух матриц), что 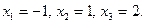
Ответ:  .
.
3. Метод Гаусса
Составим расширенную матрицу и применим к ней преобразования:
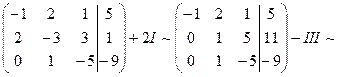

Итак, расширенная матрица с помощью элементарных преобразований сведена к ступенчатому виду. Перейдём к равносильной системе
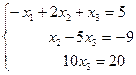 отсюда
отсюда 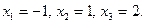
Ответ: 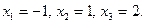
Решение задачи 4
1) Находим векторы 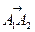 и
и 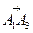 :
:
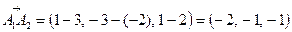
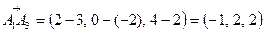
Длины этих векторов, т.е. длины рёбер  и
и  , таковы:
, таковы:

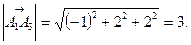
2) Найдём скалярное произведение векторов 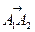 и
и 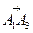
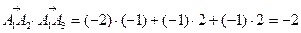
косинус угла между ними вычисляется по формуле:

Отсюда следует, что 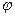 - тупой угол, равный
- тупой угол, равный 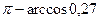 . Это и есть искомый угол между рёбрами
. Это и есть искомый угол между рёбрами  и
и  .
.
3) Площадь грани  равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах  и
и  , т.е. половине модуля векторного произведения этих векторов
, т.е. половине модуля векторного произведения этих векторов
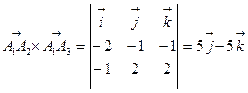 .
.
Следовательно, 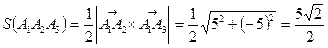 (кв.ед.)
(кв.ед.)
4) Объём пирамиды равен 1/6 объёма параллелепипеда, построенного на векторах
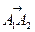 ,
, 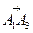 ,
,  . Вектор
. Вектор  (3, -2,4).
(3, -2,4).
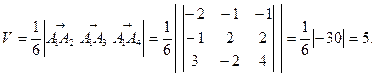 (куб. ед.)
(куб. ед.)
5) Используем способ задания плоскости через три точки:
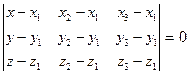 .
.
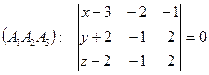 ;
;
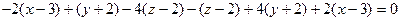
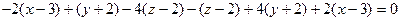
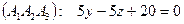 .
.
 ;
;
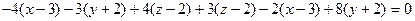
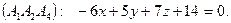
Решение задачи 5
Приведём уравнение кривой второго порядка к каноническому виду:
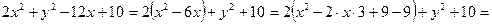
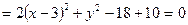
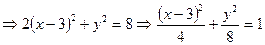
Это уравнение эллипса с центром в точке (3; 0), большой полуосью 2
и малой равной  .
.
Найдём точки пересечения прямой и эллипса, для этого надо решить следующую систему:
 .
.
Подставив вместо х в первое уравнение выражение (2-у), получим
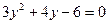 . Отсюда
. Отсюда 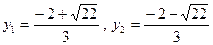 . Значения х находим, используя второе уравнение системы
. Значения х находим, используя второе уравнение системы 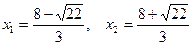 .
.
Построим графики
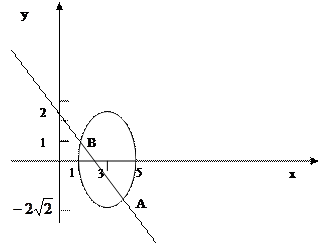 |
Ответ: рис.; 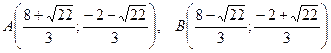 .
.
Решение задачи 6
Построить графики функций
1) 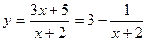 - этот график получается из графика
- этот график получается из графика 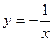 сдвигом по оси Ох на 2 единицы влево и на 3 единицы вверх по оси Оу.
сдвигом по оси Ох на 2 единицы влево и на 3 единицы вверх по оси Оу.
 |
2) 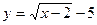 - этот график получается из графика
- этот график получается из графика 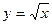 сдвигом по оси Ох на 2 единицы вправо и на 5 единиц вниз по оси Оу.
сдвигом по оси Ох на 2 единицы вправо и на 5 единиц вниз по оси Оу.
 |
Решение задачи 7
1) 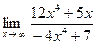 ;
;
Подстановка предельного значения аргумента приводит к неопределённости вида 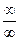 .
.
Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т.е. на 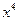 . В результате получим
. В результате получим
 , поскольку при
, поскольку при 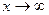 функции
функции  и
и 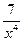 являются бесконечно малыми.
являются бесконечно малыми.
2) 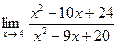 ;
;
Подстановка предельного значения аргумента приводит к неопределённости вида  . Разложим числитель и знаменатель дроби на множители. Получим
. Разложим числитель и знаменатель дроби на множители. Получим
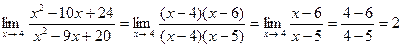 .
.
3) 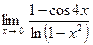 ;
;
Для раскрытия получающейся здесь неопределённости вида  используем метод замены бесконечно малых эквивалентными. Так как
используем метод замены бесконечно малых эквивалентными. Так как 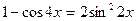 , то
, то
при 
 , а
, а
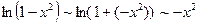 . Итак, получаем
. Итак, получаем 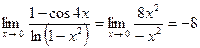 .
.
4) 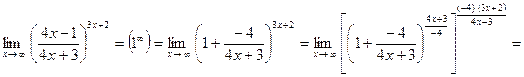
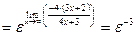 .
.
Ответ: 1) –3; 2) 2; 3) –8; 4) 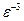
 2015-10-22
2015-10-22 1108
1108







