Примерное решение курсовой работы

Пример 1. Найти матрицу С = , где А = , B = .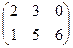

Решение: Матрицу А транспонируем

А = ; B = 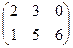; С=А+В= .

Пример 2. Решить матричное уравнение Х = .

Решение. Обозначим А = , В = 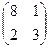. Тогда исходное уравнение принимает вид А Х = В. Имеем

Умножим обе части уравнения А Х = В слева на матрицу и получим 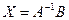. Итак .

.

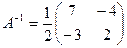Сделаем проверку:

А Х = В .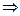

Пример 3.

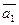Даны векторы = 3; = 4; угол между векторами и .

Вычислить

а) ;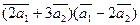

б) .

Решение:

а) Используем свойство , получаем 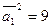и .

Используя, определение скалярного произведения получаем .

= = .

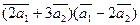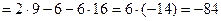б) .

Пример 4.

Даны векторы 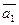(1; 2; -2) и (3; -3;0).

Вычислить

а) ;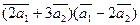

б) .

Решение:

а) Используя, свойство 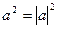получаем , .

Используя, свойство 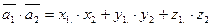получаем

= = .

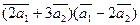б) .

Пример 6.

Составить и построить уравнения прямой, проходящей через две точки А (3;-8) и В (-2; 3).

Решение. Уравнение прямой имеет вид , откуда после преобразований получим 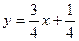- уравнение прямой с угловым коэффициентом и - общее уравнение прямой на плоскости.

Пример 7. Решить систему уравнений .

Решение: Применим метод Гаусса. Преобразуем расширенную матрицу системы .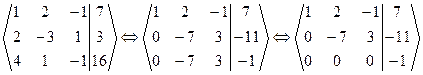

Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво, так как в результате преобразований получено неверное равенство: 0 = -1, следовательно, данная система несовместная. Система решений не имеет.