2015-10-22
308
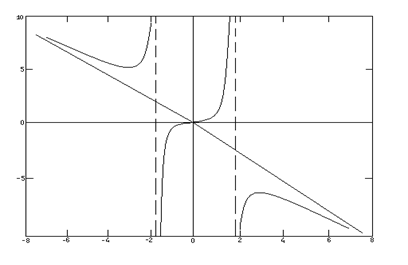
Общая схема исследования функции и построения графика.
1. Найти область определения функции.
2. Определить тип функции (четность, нечетность).
3. Найти точки пересечения с осями координат и интервалы
знакопостоянства функции.
4. Найти асимптоты графика функции:
а) вертикальные; б) невертикальные (наклонные).
5. Найти точки возможного экстремума и интервалы возрастания и
убывания функции.
6. Найти точки перегиба и интервалы выпуклости, вогнутости функции.
7. Найти дополнительные точки.
8. Построить график функции, учитывая проведенные исследования.
Пример. Исследовать функцию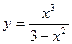 
и построить ее график.
Решение
1. 
, 
.
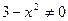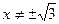Область определения функции: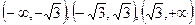 
.
Точки разрыва: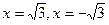 
.
2. 
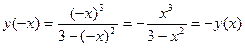. Так как 
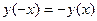, то функция нечетная. Следовательно, ее график симметричен относительно точки О.
3. 
.
| 
| 
| 
| 
| |
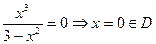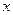
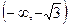
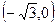
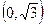
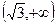
знак 
| + | - | + | - | |
| Расположение графика | Выше оси Ох | Ниже оси Ох | Пересекает ось Ох | Выше оси Ох | Ниже оси Ох |
4. а). Вертикальные асимптоты:
; 
.
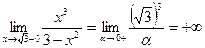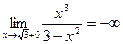Следовательно,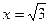 
- точка разрыва второго рода. По свойству симметрии функции 
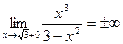. Поэтому уравнения вертикальных асимптот 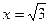и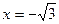 
.
Других вертикальных асимптот график не имеет.
б). Наклонные асимптоты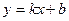 
:
;
. 
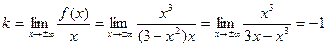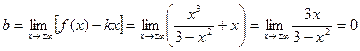Итак,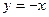 
- уравнение наклонной асимптоты графика функции.
5. 
.
, 
, 
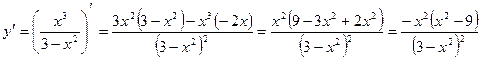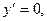
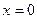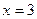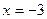- критические точки.
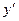не существует при 
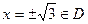, поэтому 
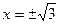не является критическими точками.
| X |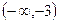 
| -3 |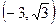 
|
|
| 
| 
| ||
|
| - | + | + | + | + | - | |||
|
|  
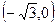
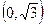
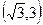
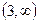
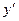
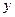
| 4,5 min |
| 
| Нет экст. | 
| 
| -4,5 max | 
|
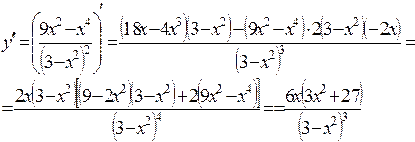
6. 
; 
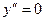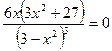при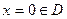 
критическая точка.
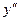не существует при 
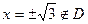. Следовательно, имеется одна критическая точка .
|
|
|
|
|
| |
|
| + | - | + | - | |
|
| 
| 
|
|
|
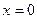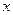
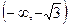
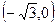
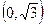
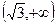
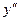
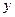
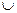
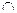
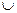
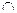
7. Дополнительные точки
|
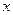
| 0,5 | 1,5 | 3,5 | |||
|
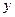
| 0,05 | 0,5 | 4,5 | -8 | -4,6 | -5 |
8.Строим график функции.
