Перпендикулярные и паралельные прямые

Теорема - высказывание, правильность которого установлена при помощи рассуждения, доказательства. Примером теоремы может служить утверждение о том, что сумма величин углов произвольного треугольника равна 180°. Проверить это можно было бы опытным путем: начертить треугольник, измерить транспортиром величины его углов и, сложив их, убедиться, что сумма равна 180° (во всяком случае, в пределах той точности измерения, которую допускает транспортир). Такую проверку можно было бы повторить несколько раз для различных треугольников. Однако справедливость этого утверждения устанавливается в курсе геометрии не опытной проверкой, а при помощи доказательства, которое убеждает нас в том, что это утверждение справедливо для любого треугольника. Таким образом, утверждение о сумме углов треугольника является теоремой.

В формулировках теорем, как правило, встречаются слова «если..., то...», «из... следует...» и т.д. В этих случаях для сокращения записи используют знак 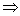. Возьмем в качестве примера теорему о том, что точка 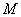, одинаково удаленная от двух точек 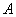и 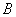, принадлежит оси симметрии этих точек (рис. 1). Ее можно подробнее сформулировать так: (для любых точек 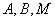) 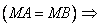( 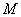принадлежит оси симметрии точек 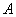и ).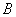

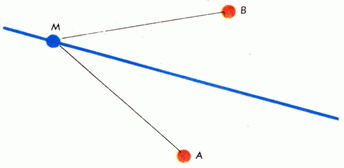
Рис. 1

Аналогичным образом могут быть записаны и другие геометрические теоремы: сначала идет разъяснительная часть теоремы (описывающая, какие точки или фигуры рассматриваются в теореме), а затем - два утверждения, соединенные знаком 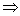. Первое из этих утверждений, стоящее после разъяснительной части и перед знаком 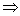, называется условием теоремы, второе, стоящее после знака 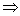, называется заключением теоремы.

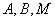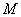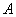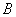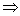
Меняя местами условие и заключение и оставляя без изменения разъяснительную часть, мы получаем новую теорему, которая называется обратной первоначальной. Например, для рассмотренной выше теоремы обратной будет следующая: (для любых точек ) (точка принадлежит оси симметрии точек и ) 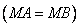. Короче: если точка 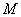принадлежит оси симметрии точек 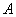и 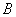, то точка 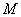одинаково удалена от точек 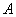и 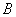. В данном случае и исходная теорема, и обратная ей теорема справедливы.

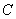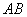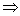
Однако из того, что некоторая теорема верна, не всегда следует, что обратная ей теорема также верна. Например, теорема: (точка не принадлежит прямой ) 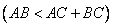справедлива, но обратная ей теорема: 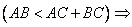(точка 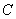не принадлежит прямой 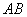) - неверна, так как при условии 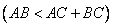точка 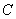может быть расположена на прямой 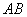, но вне отрезка 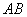(рис. 2).

Рис. 2

Таким образом, доказав некоторую теорему, мы еще не можем утверждать, что верна и обратная теорема. Справедливость обратной теоремы требует отдельного доказательства.

В алгебре примерами теорем могут служить различные тождества, например равенства:

,

,

.

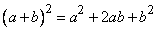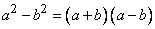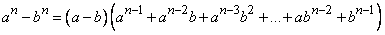Они выводятся (доказываются), исходя из аксиом, и потому являются теоремами. Другим примером теорем в алгебре может служить теорема Виета о свойствах корней квадратного уравнения.

Большую роль в математике играют так называемые теоремы существования, в которых утверждается лишь существование какого-либо числа, фигуры и т.п., но не указывается, как это число (или фигура) могут быть найдены. Например: всякое уравнение 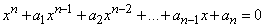с действительными коэффициентами имеет при нечетном 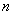хотя бы один действительный корень, т.е. существует число 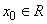, являющееся корнем этого уравнения.

Некоторым видам теорем дают особые названия, например лемма, следствие. Они имеют дополнительный оттенок. Леммой обычно называют вспомогательную теорему, саму по себе мало интересную, но нужную для дальнейшего. Следствием называют утверждение, которое может быть легко выведено из чего-то ранее доказанного.

Иногда теоремой называют то, что правильнее было бы называть гипотезой. Например, «великая теорема Ферма» (см. Ферма великая теорема), утверждающая, что уравнение 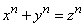не имеет целых положительных решений при 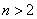, пока не доказана.

Посмотрите вокруг. Как много разных предметов окружает нас в нашей жизни! Большие и маленькие, светлые и темные, деревянные и металлические. И люди вокруг нас отличаются друг от друга. Взрослые и малыши, высокие и низкие, мальчики и девочки. Вот две книги на моем столе. У них, казалось бы, так много общего. Назовите, чем они похожи? (материал, форма) И все-таки они разные. Чем они отличаются друг от друга? (размер)
Вы сказали о материале, форме, размере этих книг. Как назвать эти понятия одним словом? (признаки) А что такое признак предмета?
Признак – это отличительная черта, та особенность, которая отличает этот предмет от сотен и тысяч ему подобных.
— А по каким признакам можно сгруппировать предметы? (цвет, форма и т.д.)

На уроках, чтобы объяснить, чем отличается свойство от признака, кажется, можно обойти противоречия с нематематической терминологией, вводя не очень-то распространённое понятие «характеристика», которое дети будут понимать как «перечисление черт объекта, отвечающих на вопрос «Какой?»». При этом одна и та же характеристика может играть роль необходимого условия (свойства) или достаточного условия (признака) в зависимости от того, служит она для описания наблюдаемого объекта или для идентификации его в некотором множестве объектов.
Это можно подать, например, в виде игры, когда двое учащихся становятся друг к другу спиной. Перед ними одинаковые наборы фигур. Первому предлагается взять фигуру и, не произнося её название, описать такие её черты, по которым второй найдет её в своём наборе. Для первого называемые характеристики будут свойствами наблюдаемой им фигуры, а для второго – признаками в нематематическом смысле, по которым эту фигуру нужно идентифицировать. При этом достаточный для идентификации признак (или совокупность признаков) можно будет назвать характеристическим признаком и объяснить, что математики именно его и только его и называют признаком. Первый ученик вполне обоснованно назовёт соответствующее свойство аналогично – характеристическим свойством.