Опорный конспект
1. Определение степени с целым отрицательным показателем
Если а≠0, n – натуральное число, то а-n = 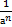
Например,
1) 3-2= 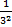 =
= 
2)  =
= 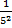 = 5-2
= 5-2
2. Если  ≠0, и n – натуральное число, то
≠0, и n – натуральное число, то  -n
-n 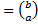 n
n
Например, 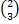 -2 =
-2 = 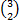 2 =
2 =  = 2
= 2 
Замечание. Если а ≠ 0, то а 0 = 1
3. Найти значения выражения
 -1 + 9-2 - (-2,6) 0 =
-1 + 9-2 - (-2,6) 0 =
Шаг 1. Замените степени с отрицательным показателем на степени с натуральным показателем:
=  +
+ 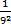 - (-2,6) 0 =
- (-2,6) 0 =
Шаг 2. Выполните возведение в степень
=  +
+ 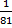 - 1 =
- 1 =
Шаг 3. Выполните действия с дробями:
= 2  - 1 +
- 1 + 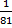 = 1
= 1 
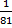 = 1
= 1  +
+ 
4. Свойства степени с целым отрицательным показателем
Если m и n целые числа, а 
1) a m  а n = am+n
а n = am+n
2) a m 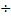 а n = am-n
а n = am-n
3) (am)n = amn
4) (ab)m = am bm
5) 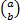 n =
n = 
5. Применение свойств степени с целым отрицательным показателем
Пример 1. Упростить
6 х-2с 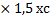 -3 = 6
-3 = 6 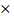 1,5
1,5 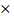 Х-2
Х-2  -3 = 9Х-1
-3 = 9Х-1 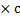 -2 = 9
-2 = 9 
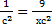
III. Закрепление изученного материала
1. Открыть учебник алгебры, параграф 10, стр. 96 – 97 прочитать и записать определение степени с произвольным целым показателем стр.97.
2. Самостоятельно в тетрадях выполнить следующие задания
1-й вариант решает 1, 3, 5 столбцы
2-1 вариант решает 2, 4, 6 столбцы
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | (-5) -2 | -5-2 | (-2  )2 )2
| 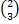 2 2
| -(2  )-2 )-2
| 23  -7 -7
|
| 2 | 63 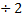
| (6  3 3
| -3 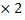 -2 -2
| -62  (-10)-1 (-10)-1
| (-0,4)2 | 53 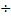 52 52
|
| 3 | (-1) -100 | -10-2 | (-1)-201 | -0,42 | 05 | (32 а)5 |
| 4 | 2 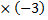 2 2
| -5 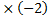 2 2
| 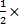 (-4)2 (-4)2
| -  (-3)2 (-3)2
| -  (-3)2 (-3)2
| (2  -1)2 -1)2
|
| 5 | 72 +3-3 | 10-5 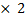 -3 -3
| (6+2)-2 | 102 -32 | 62-(-1)3 | (2ав)-3 |
IV. Домашние задание: параграф 10, стр.96-98, знать определение степени с отрицательным показателем т свойства степени, ответить на вопросы 1-6 на стр.98 устно, решить задание с таблицы свой вариант.
 2015-10-22
2015-10-22 644
644






