Примеры для самостоятельного решения

1. Решить системы линейных уравнений

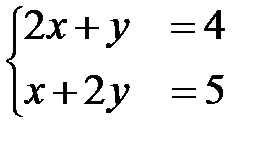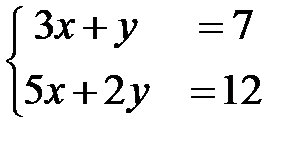1) ; 2) ; 3)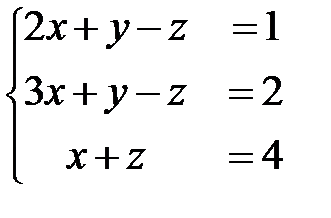

4) 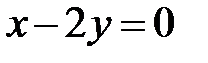; Ответ: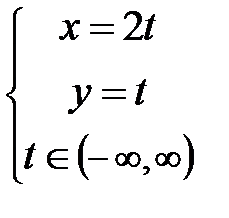

5) 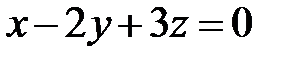; Ответ: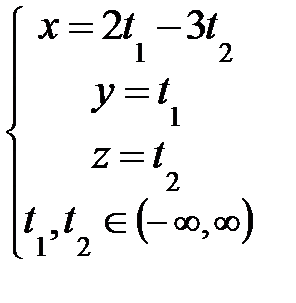

6) 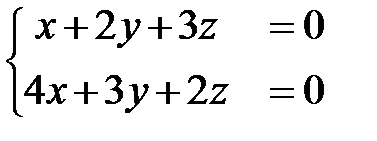; Ответ: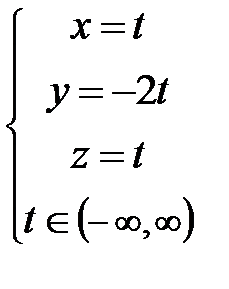

7) 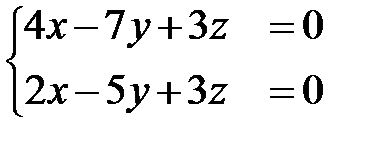; Ответ: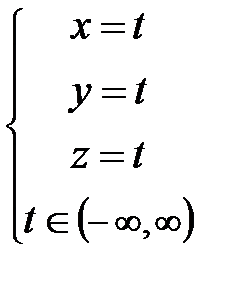

8) 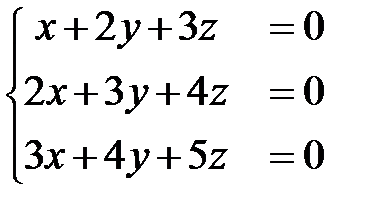; Ответ: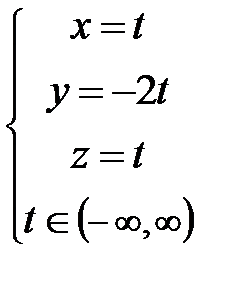

9) 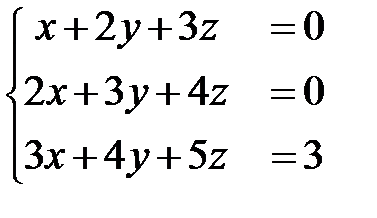; Ответ: Решений нет

10) 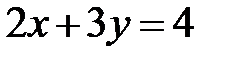; Ответ: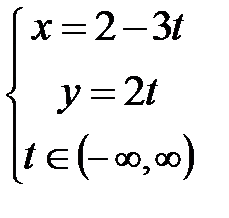

11) 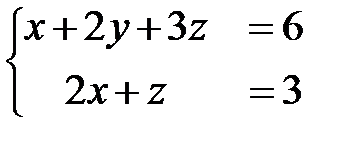; Ответ: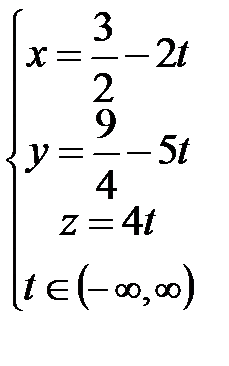

12) 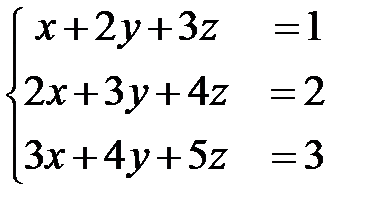; Ответ: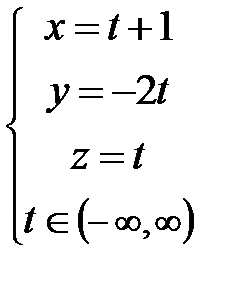

2. Проверить с помощью определителя линейную зависимость следующих систем столбцов

1) = , = , =

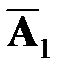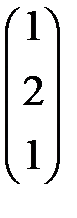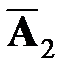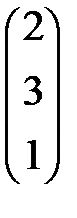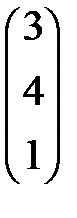
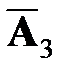2) = , = , =

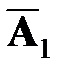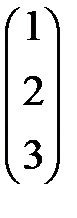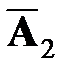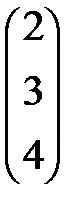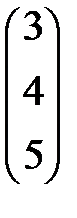
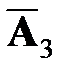3. Решить матричное уравнение

=

Практические занятия.

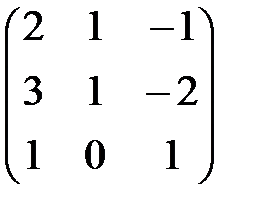
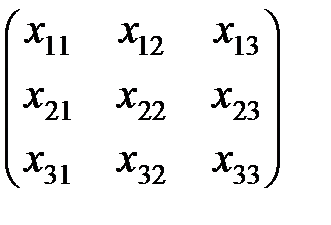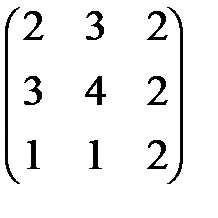
Практическое занятие № 1 Выполнение операций над матрицами.

Тема программы: Матрицы и определители.

Цель работы: научиться выполнять операции над матрицами.

Время выполнения: 2 часа.

Теоретические основы

Матрицы

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде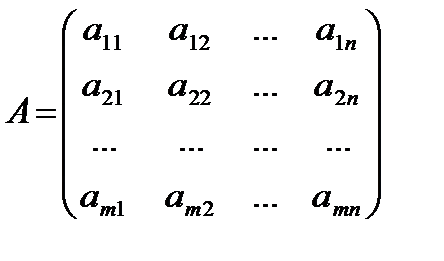

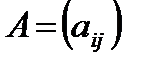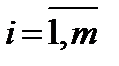или, сокращенно, , где (т.е. 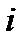=1,2,3,…, m) – номер строки, 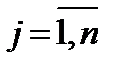(т.е. 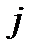=1,2,3,…, n) – номер столбца.

Матрицу 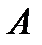называют матрицей размера 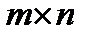и пишут 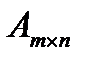. Числа 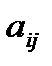, составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из левого верхнего угла, образуют главную диагональ матрицы.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е. 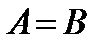, если 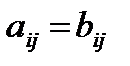, где , .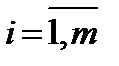

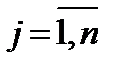Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера 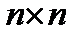называют матрицей 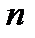-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой .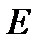

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой .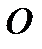

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка, соответственно).

Замечание: каждой квадратной матрице 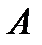можно поставить в соответствие определенное число, называемое определителем (детерминантом) этой матрицы. Неквадратная матрица определителя не имеет.

Определители

Определители 2-го порядка

Определитель (или иначе, детерминант) обозначается следующим образом: .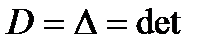

Простейшие из определителей – это так называемые определители 2-го порядка.

Определителем второго порядка, называется число, которое вычисляется по формуле: .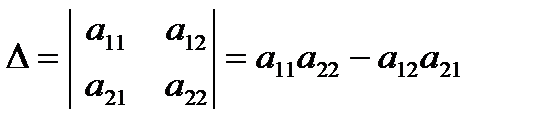

Элементы 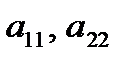образуют главную диагональ , 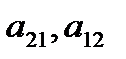– побочную. Вычисление определителя 2-го порядка иллюстрируется схемой: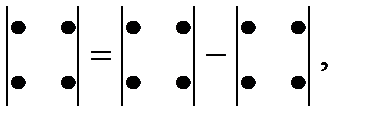

т.е. из произведения элементов главной диагонали вычитается произведение элементов побочной.

Основные свойства определителей.

1. Определитель не изменится, если его строки заменить столбцами, и наоборот.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых ряда равен нулю.

4. Если все элементы одного ряда умножить на некоторое число k, то весь умножится на это число.

Это свойство можно сформулировать иначе:

Общий множитель элементов какого-либо ряда можно вынести за знак .

5. Если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой равен 0.

6. Если элементы какого-либо ряда представляют собой

суммы двух слагаемых, то может быть разложен на сумму двух соответствующих определителей.

7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

Определители 3-го порядка

Определителем третьего порядка, называется число, которое вычисляется по формуле:

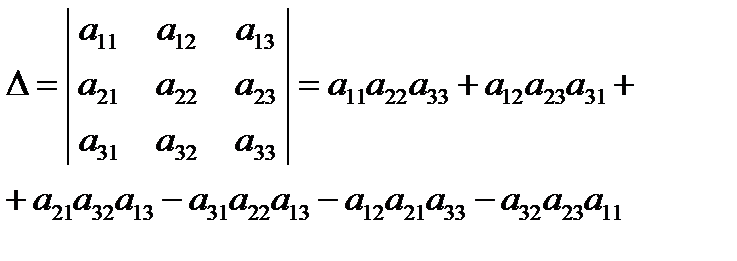
Элементы 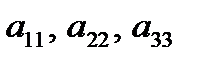образуют главную диагональ определителя, элементы 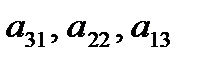- побочную.

Для нахождения значения определителя 3-го порядка удобно пользоваться правилом треугольников, которое символически можно записать так:

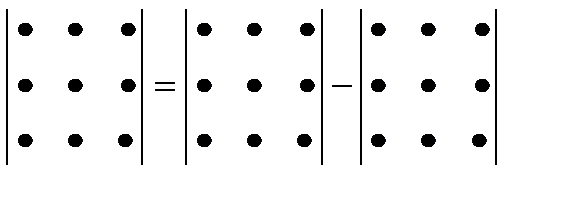
Определитель 3-го порядка представляет собой алгебраическую сумму шести произведений, причем три произведения берутся со знаком „ + “ и три – со знаком „ – “. Со знаком „ + “ берется произведение элементов, стоящих на главной диагонали, а также произведения элементов, стоящих на параллели к главной диагонали, с добавлением третьего множителя из противоположного угла таблицы. Со знаком „ – “ берется произведение элементов, стоящих на побочной диагонали, а также произведения элементов, стоящих на параллели к побочной диагонали, с добавлением третьего множителя из противоположного угла таблицы.

Определители n-го порядка

Определителем n -го порядка называется число, равное алгебраической сумме 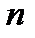! членов, каждый из которых является произведением 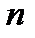элементов матрицы, взятых по одному из каждой строки и каждого столбца.

Заметим, что с ростом 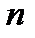резко увеличивается число членов определителя (n!), поэтому даже для 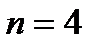использование формулы весьма трудоемко (получим 24 слагаемых!).

На практике при вычислении определителей высоких порядков используют другие формулы. Для их рассмотрения необходимо ввести новые понятия.

Минором некоторого элемента 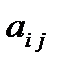определителя n-го порядка называется определитель (n-1)- го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается .

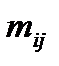Так, если 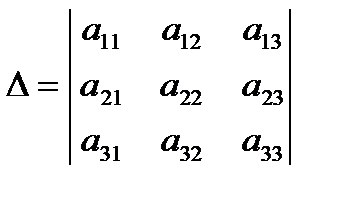, то .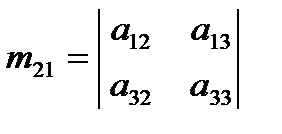

Алгебраическим дополнением элемента 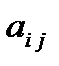определителя называется его минор, взятый со знаком 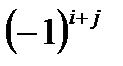, где i – номер строки, j – номер столбца, на пересечении которых находится выбранный элемент. Обозначается: . .

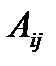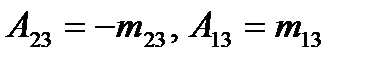Теорема: Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

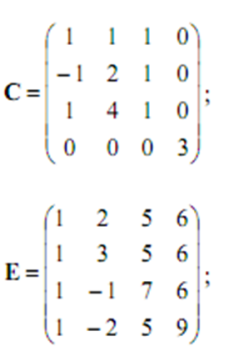Практическое задание

Вариант 1

1. Запишите элемент С₂₄ матрицы С

2. Вычислите минор М₄₄

3. Вычислить алгебраическое дополнение С₁₁

4. Вычислить произведение элементов главной диагонали

5. Разложите определитель по 3-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 2 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 2

1. 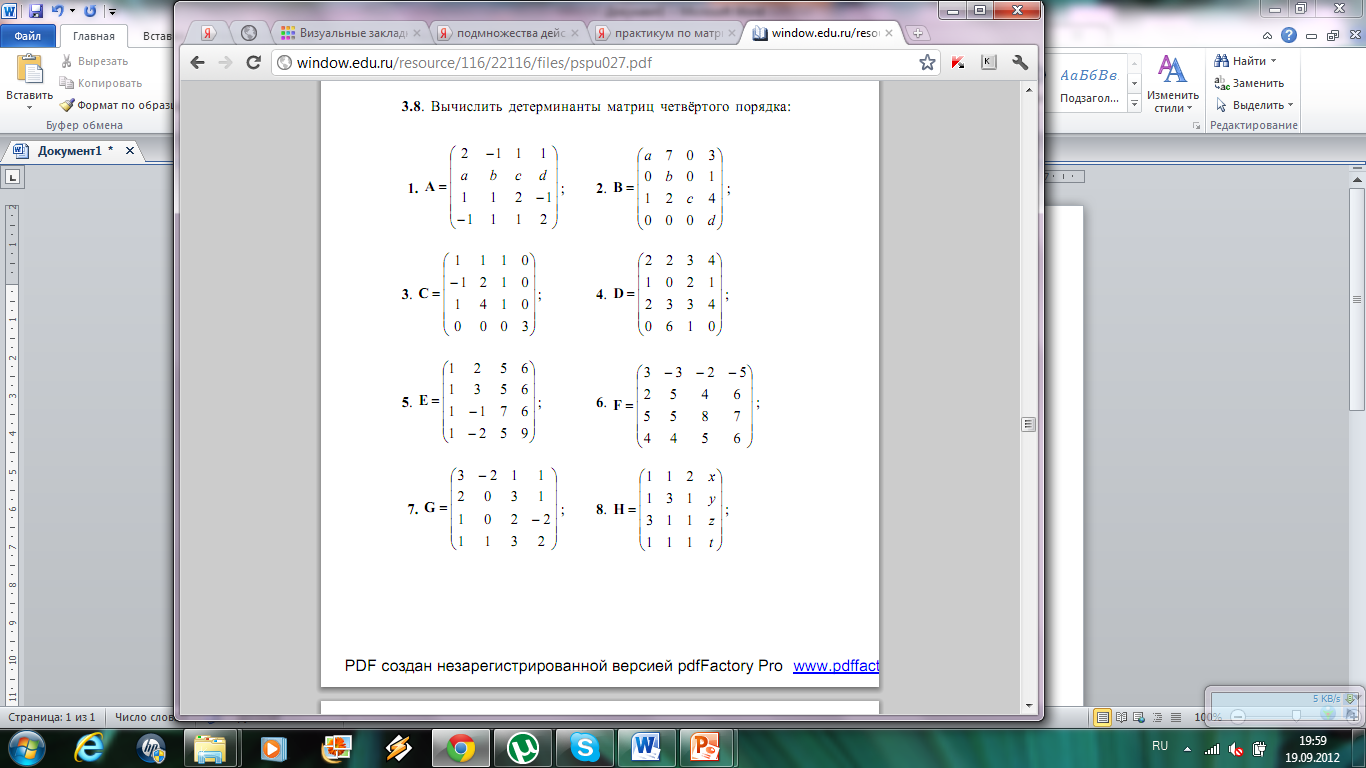Запишите элемент Е₁₄ матрицы Е

2. Вычислите минор Е₂₃

3. Вычислить алгебраическое дополнение Е₃₁

4. Вычислить произведение элементов побочной диагонали

5. Разложите определитель по 2-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 4 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 3

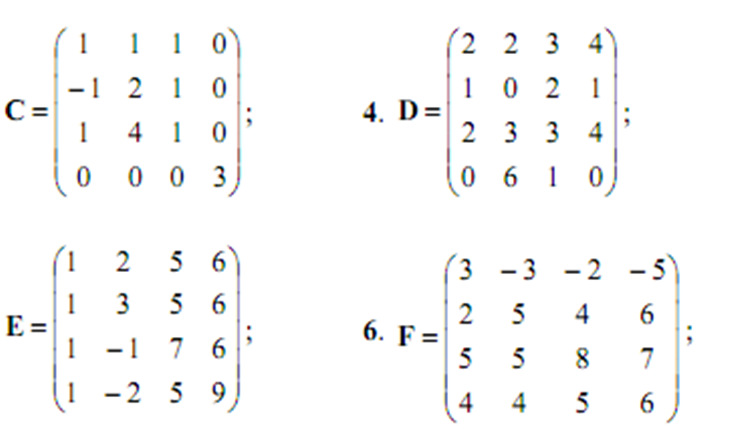1. Запишите элементD₁₂ матрицы D

2. Вычислите минор D₃₁

3. Вычислить алгебраическое дополнение D₂₃

4. Вычислить произведение элементов побочной диагонали

5. Разложите определитель по 1-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 3 –у столбцу, через алгебраические дополнения (не вычисляя).

Вариант 4

1. 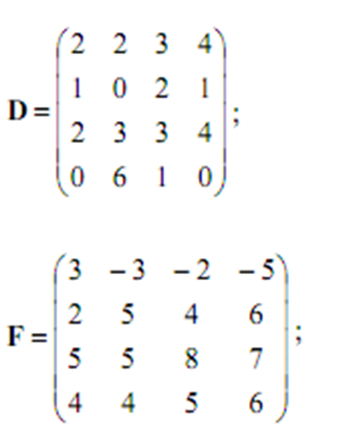Запишите элемент F₂₂ матрицы F

2. Вычислите минор F₄₁

3. Вычислить алгебраическое дополнение F₁₄

4. Вычислить произведение элементов главной диагонали

5. Разложите определитель по 4-й строчке, не вычисляя полученные определители.

6. Разложите определитель по 1 –у столбцу, через алгебраические дополнения (не вычисляя).

Практическое занятие № 2 Решение систем линейных уравнений по формулам Крамера.

Тема программы: Системы линейных уравнений

Цель работы: научиться решать системы линейных уравнений по формулам Крамера.

Время выполнения: 2 часа.

Теоретические основы

Определители впервые были введены для решения системы уравнений первой степени. В 1750г. швейцарский математик г. Крамер дал общие формулы, выражающие неизвестные через определители, составленные из коэффициентов системы.

Рассмотрим систему трех уравнений первой степени с тремя неизвестными :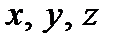

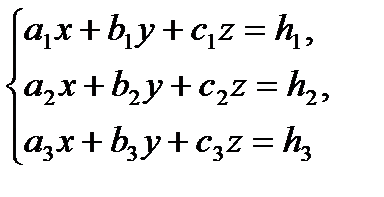
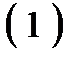
(коэффициенты 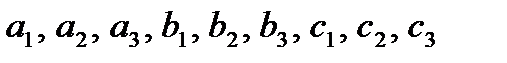и свободные члены 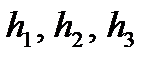считаются заданными).

Тройка чисел 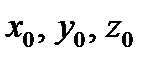называется решением системы 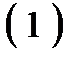, если в результате подстановки этих чисел вместо 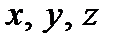все три уравнения 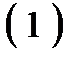обращаются в тождество.

В дальнейшем основную роль будут играть следующие четыре определителя:

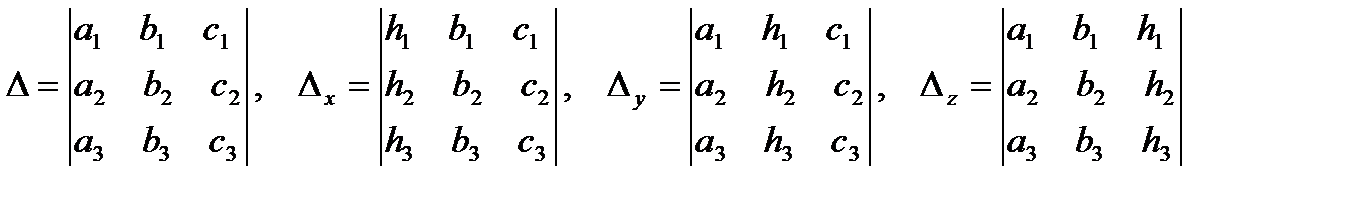
Определитель называется определителем системы 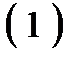. Определители 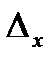, , 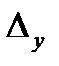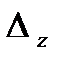получаются из определителя системы заменой свободными членами элементов соответственно первого, второго и третьего столбцов.

Возможны три случая:

1) Если определитель системы 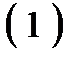отличен от нуля (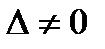), то существует, и притом единственное, решение этой системы и оно выражается формулами 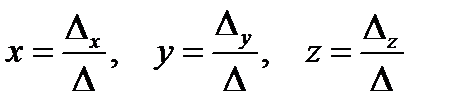(формулы Крамера)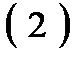

2) Если определитель системы 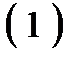равен нулю (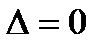) и хотя бы один из определителей 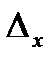, , 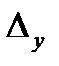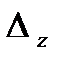отличен от нуля, то система не имеет решения (несовместна).

3) Есл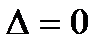и и 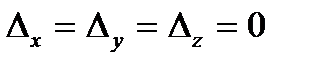, то система 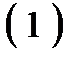либо совсем не имеет решений, либо если система 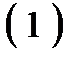имеет хотя бы одно решение, то она имеет бесконечно много решений. В этом случае, одно из трех уравнений является следствием двух других. Система сводится к двум уравнениям с тремя неизвестными и имеет бесчисленное множество решений.

Практические задания

ВАРИАНТ 1.

Решить системы:

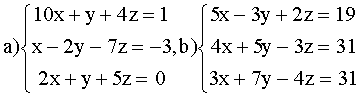
ВАРИАНТ 2.

Решить системы:

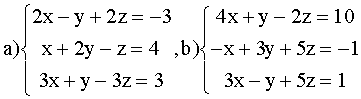
ВАРИАНТ 3.

Решить системы:

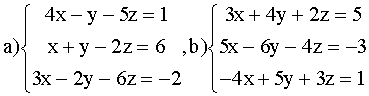
ВАРИАНТ 4.

Решить системы:

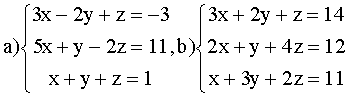
ВАРИАНТ 5.

Решить системы:

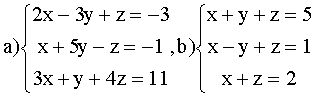
ВАРИАНТ 6.

Решить системы:

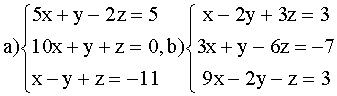
ВАРИАНТ 7.

Решить системы:

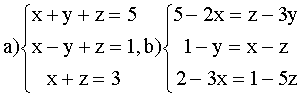
ВАРИАНТ 8.

Решить системы:

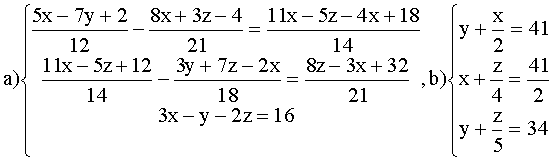
Практическое занятие № 3 Решение систем линейных уравнений методом обратной матрицы.

Тема программы: Системы линейных уравнений

Цель работы: научиться решать системы линейных уравненийметодом обратной матрицы.

Время выполнения: 2 часа.

Теоретические основы

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию 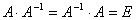. (Это определение вводится по аналогии с умножением чисел)

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Доказательство:

1. Необходимость. Пусть для матрицы A существует обратная матрица A^-1. Покажем, что | A | ≠ 0.

Прежде всего заметим, что можно доказать следующее свойство определителей .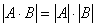

Предположим, что | A | = 0. Тогда 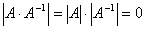. Но с другой стороны 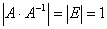. Полученное противоречие и доказывает, что | A | ≠ 0.

2. Достаточность. Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть и | A | ≠ 0.

Покажем, что в этом случае обратной матрицей будет матрица

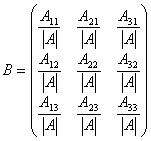, где A_ij алгебраическое дополнение элемента a_ij.

Найдём AB=C.

Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,

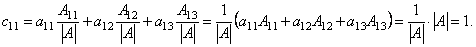
Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c₂₂ = c₃₃ = 1.

Кроме того, все недиагональные элементы матрицы C равны нулю. Например,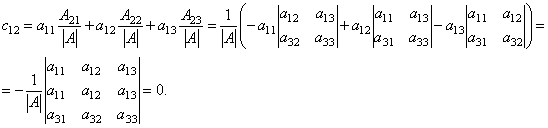

Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A^-1.

Таким образом, теорема содержит способ нахождения обратной матрицы.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

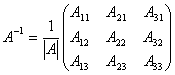где A_ij - алгебраические дополнения элементов a_ij данной матрицы A.

Итак, чтобы найти обратную матрицу нужно:

1. Найти определитель матрицы A.

2. Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу 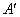, элементами которой являются числа A_ij.

3. Найти матрицу, транспонированную полученной матрице 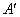, и умножить её на 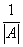– это и будет .

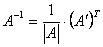Аналогично для матриц второго порядка, обратной будет следующая матрица .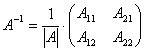

Примеры.

1. Найти матрицу, обратную данной 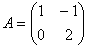. Сделать проверку.

| A | = 2. Найдем алгебраические дополнения элементов матрицы A.

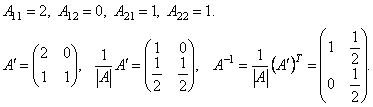
Проверка:

.

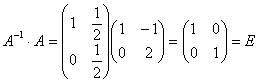Аналогично A∙A^-1 = E.

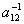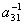2. Найти элементы и матрицы A^-1 обратной данной

.

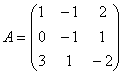Вычислим | A | = 4. Тогда .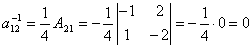

.

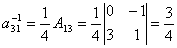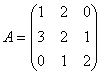. Найдем обратную матрицу.

Практические задания

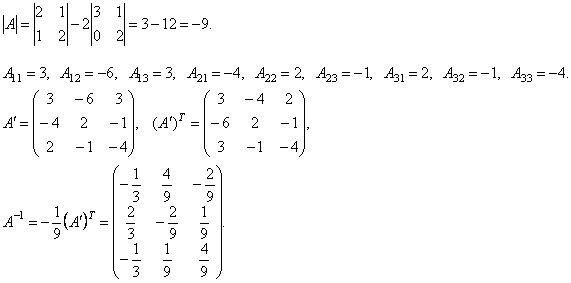
Практическое занятие № 4 Система т линейных уравнений с п переменными. Решение систем линейных уравнений методом Гаусса.

Тема программы: Системы линейных уравнений

Цель работы: отработать навыки решения систем линейных уравнений методом Гаусса.

Время выполнения: 2 часа.

Теоретические основы

Наиболее распространенным точным методом решения системы линейных уравнений является метод Гаусса. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему.

Пусть дана произвольная система линейных уравнений:

а₁₁х₁+ а₁₂х₂+...+ а_1пх_п = b ₁,

(1)

а₂₁х₁+ а₂₂х₂+...+ а_2пх_п = b ₂,

........................................

а _{s 1}х₁+ а _{s 2}х₂+...+ а_sпх_п = b_s.

Будем производить над ней элементарные преобразования. Для этого выпишем матрицу из коэффициентов при неизвестных системы (1) с добавлением столбца свободных членов, другими словами расширенную матрицу Ā для системы (1):

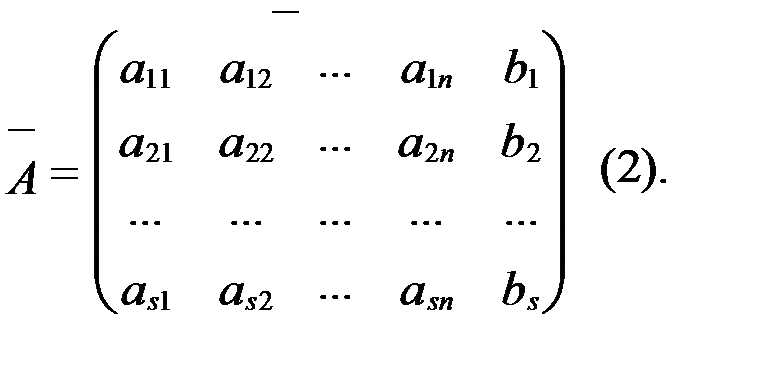
Предположим, что с помощью таких преобразований удалось привести матрицу Ā к виду:

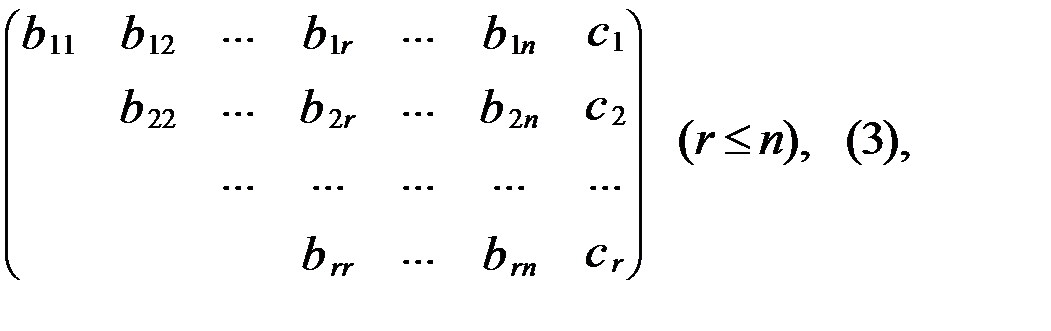
где все диагональные элементы b ₁₁, b ₂₂,..., b_rr отличны от нуля, а элементы, расположенные ниже диагональных, равны нулю. Матрице (3) соответствует система уравнений:

b₁₁x₁+b₁₂x₂+...+b_1rx_r+...+b_1nx_n=c₁,

(4),

b₂₂x₂+...+b_2rx_r+...+b_2nx_n=c₂,

......................................

b_rrx_r+...+b_rnx_n=c_r,

которая получается из системы (1) с помощью некоторого числа элементарных преобразований и, следовательно, равносильна системе (1). Если в системе (4) r=n, то из последнего уравнения, имеющего вид b_nnx_n=c_n (где b_nn ≠ 0), находим единственное значение x_n, из предпоследнего уравнения – значение x_n-1 (поскольку x_n уже известно) и т.д., наконец, из первого уравнения – значение x ₁. Итак, в случае) r=n система имеет единственное решение. Если же r<n, то система (4) легко приводится к системе вида:

х₁=a₁, _{r +1}х _{r +1}+...+a_{1 n} х _n +b₁,

r<n,

(5),

х₂=a₂, _{r +1}х _{r +1}+...+a_{2 n} х _n +b₂,

............................................

х _r =a _r, _{r +1}х _{r +1}+...+a _{r n} х _n +b _r.

которая и является по существу общим решением системы (1).

Неизвестные х _{r +1},..., х _n называются свободными. Из системы (5) можно будет найти значения х₁,..., х _r.

Приведение матрицы Ā к виду (3) возможно только в том случае, когда исходная система уравнений (1) совместна. Если же система (1) несовместна, то такое приведение невозможно. Это обстоятельство выражается в том, что в процессе преобразований матрицы Ā в ней появляется строка, в которой все элементы равны нулю, кроме последнего. Такая строка соответствует уравнению вида:

0*х₁+0*х₂+...+0*х _n = b,

которому не удовлетворяют никакие значения неизвестных, так как b ≠0. В этом случае система несовместна.

В процессе приведения системы (1) к ступенчатому виду могут получаться уравнения вида 0=0. Их можно отбрасывать, так как это приводит к системе уравнений, эквивалентных прежней.

При решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя все преобразования над её строками. Последовательно получающиеся в ходе преобразований матрицы обычно соединяют знаком эквивалентности.

Решим следующую систему уравнений с 4-мя неизвестными:

2х₁+5х₂+4х₃+х₄=20,

х₁+3х₂+2х₃+х₄=11,

2х₁+10х₂+9х₃+7х₄=40,

3х₁+8х₂+9х₃+2х₄=37.

Выпишем расширенную матрицу из коэффициентов при неизвестных с добавлением столбца свободных членов.

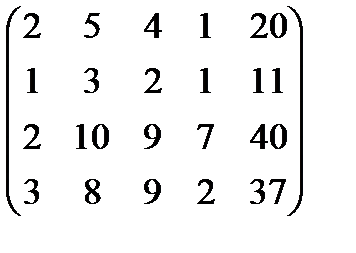
Произведём анализ строк расширенной матрицы:

- к элементам 2-ой строки прибавим элементы 1-ой, делённые на (-2);

- из 3-ей строки вычтем 1-ю строку;

- к 4-ой строке прибавим 1-ю, умноженную на (-3/2).

В качестве вычислительного средства воспользуемся инструментами программы табличный редактор.

1. Включите компьютер.

2. Подождите пока загрузится операционная система Windows, после чего откройте окно табличного редактора.

3. 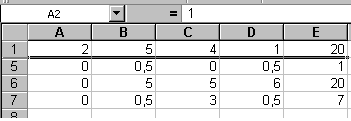Заполните ячейки таблицы значениями расширенной матрицы (рис. 11.1)

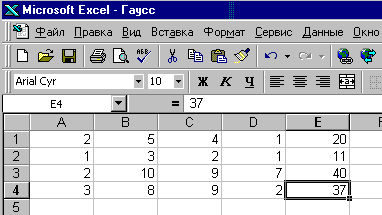
Рис. 11.1 Рис. 11.2

4. Для выполнения выбранного словесного алгоритма производим следующие действия.

· Активизируйте ячейку А5 и с клавиатуры занесите в неё формулу вида =А2+А1/(-2), после чего автозаполнением занесите численные результаты в ячейки В5¸Е5;

· В ячейке А6 разместим результат вычитания 1-ой строки из 3-ей, и снова, пользуясь автозаполнением, заполним ячейки В6¸Е6;

· в ячейке А7 запишем формулу вида =А4+А1*(-3/2) и автозаполнением занесём численные результаты в ячейки В7¸Е7.

· Далее скроем 2, 3 и 4 – строки, которые нам уже не нужны. Для этого воспользуемся пунктом меню ФОРМАТ®СТРОКА®СКРЫТЬ (см.§ 6). Результат показан на рис. 11.2.

5. Снова произведём анализ строк получившихся в результате элементарных преобразований матрицы, чтобы привести её к треугольному виду.

· К 6-ой строке прибавим 5-ю, умноженную на число (-10);

· из 7-ой строки вычтем 5-ю.

Записанный алгоритм реализуем в ячейках А8, А9, после чего скроем 6 и 7 – строки (см. рис. 11.3).

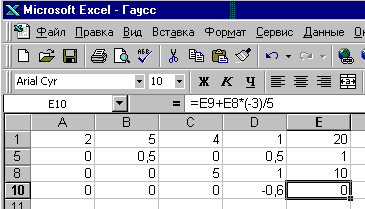
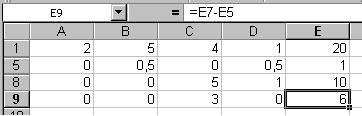
Рис. 11.3 Рис. 11.4

6. И последнее, что нужно сделать, чтобы привести матрицу к треугольному виду – это к 9-ой строке прибавить 8-ю, умноженную на (-3/5), после чего скрыть 9-ю строку (рис. 11.4).

Как вы можете видеть, элементы получившейся матрицы находятся в 1, 5, 8 и 10 строках, при этом ранг получившейся матрицы r = 4, следовательно, данная система уравнений имеет единственное решение. Выпишем получившуюся систему:

2х₁+5х₂+4х₃+ х₄ =20,

0,5х₂ + 0,5х₄=1,

5х₃+х₄ =10,

-0,6х₄=0.

Из последнего уравнения легко находим х₄=0; из 3-го уравнения находим х₃=2; из 2-го – х₂=2 и из 1-го – х₁=1 соответственно.

Практические задания

Методом Гаусса решите системы уравнений: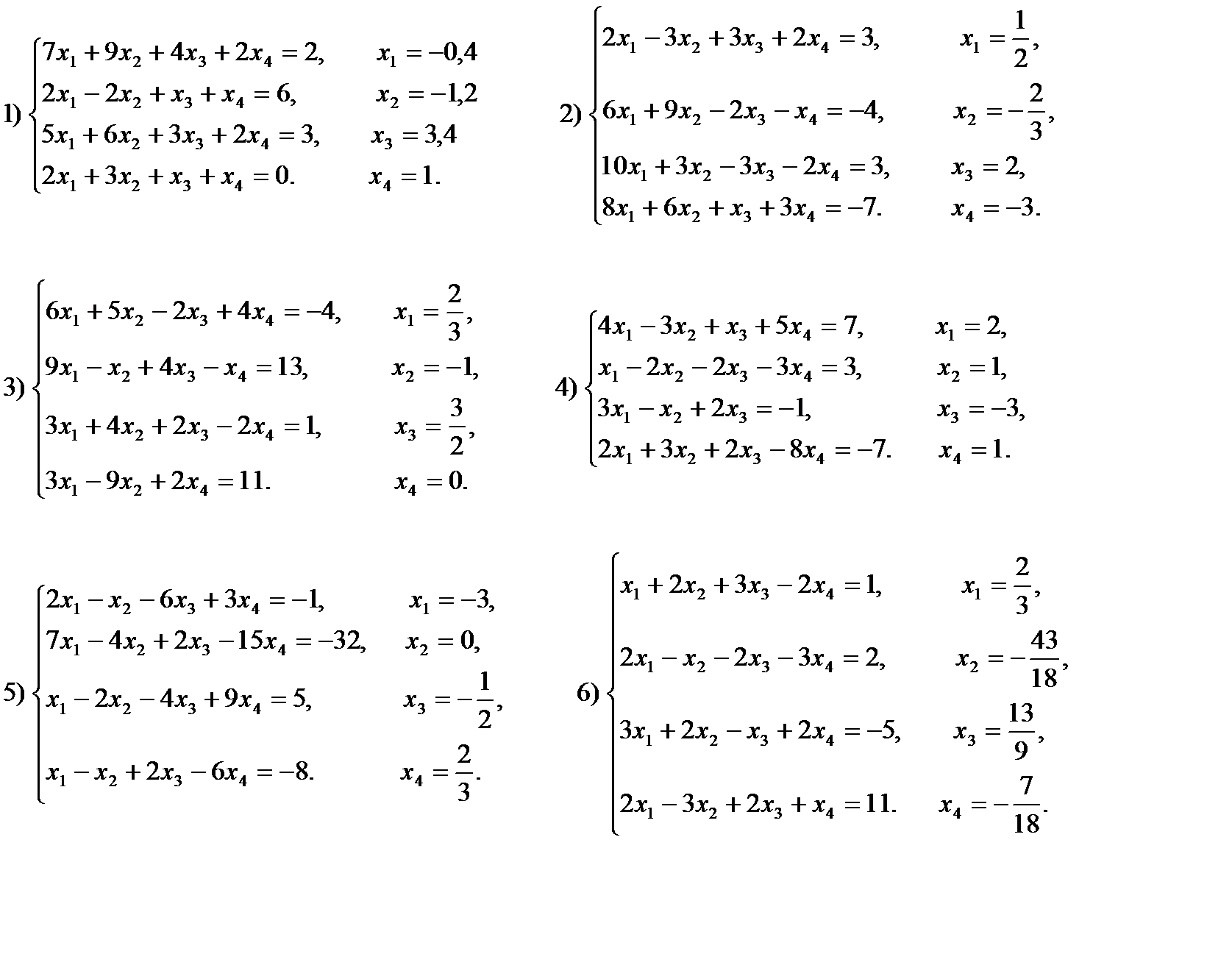

Практическое занятие № 5 Решение систем линейных уравнений.

Тема программы: Системы линейных уравнений

Цель работы: отработать навыки в решении систем линейных уравнений различными способами.

Время выполнения: 2 часа.

Теоретические основы