2015-10-22
313Алгебра, 9 класс
Задания по работе 5
Тема 3: «Системы уравнений»
| № задания | Задание |
| Какая пара является решением системы уравнений х2 + у2 – 2 = 27, 2х + у = - 12? | |
| а | (- 5; - 2); |
| б | (- 5; - 8); |
| в | (- 3; 6); |
| г | (-4; - 4). |
| Решите систему уравнений х2 + у2 = 5, х + у = 3. | |
| а | (5; 2); |
| б | (5; 8); |
| в | (3; 6); |
| г | (2; 1), (1; 2). |
Определите с помощью графиков число решений системы уравнений
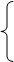 у =  ,
у = х2 – 4.
| |
| а | |
| б | |
| в | |
| г | ни одного |
Сколько решений имеет система уравнений
 х2 + у2 = 9,
у = 2 - х2.
| |
| а | |
| б | |
| в | |
| г | |
| Найдите координаты всех точек пересечения параболы у = х2 – 4х + 1 и прямой у = х – 3, не выполняя построения графиков. | |
| а | (5; 2); |
| б | (1; -2), (4; 1); |
| в | (3; 6); |
| г | (2; 1), (1; 2). |
Решить систему уравнений  методом сложения и найти произведение компонентов решения.
| |
| а | |
| б | |
| в | |
| г | 
|
Решить систему уравнений методом сложения 
| |
| а | (3; 4) |
| б | (2;-4) |
| в | (7; 9) |
| г | (0;-5) |
| Разность двух положительных чисел равна 4, а их произведение равно 12. Найдите их сумму. | |
| а | |
| б | |
| в | |
| г | |
| Длина диагонали прямоугольника равна 5, а его площадь 12. Найдите стороны прямоугольника. | |
| Площадь прямоугольника, одна из сторон которого на 2 см больше другой, равна 35 см². Найдите периметр прямоугольника. | |
| Периметр прямоугольника равен 28 см, а его площадь равна 40 см². Найдите стороны прямоугольника. | |
| Гипотенуза прямоугольного треугольника равна 13 см. Найдите его катеты, если один из них на 7 см больше другого. | |
| Произведение двух чисел равно на 29 больше их суммы. Если к первому числу прибавить удвоенное второе число, то получится 19. Найдите эти числа. | |
| При каких значениях k парабола у= -х²-3 и прямая у= kх имеют только одну общую точку? |
