Основные понятия сходимости числовых рядов

Лекция №7

Числовым рядом называется выражение вида , где являются членами числового ряда и представляют собой действительные или комплексные числа.

Числовой ряд задается с помощью формулы общего члена ряда , описывающей зависимость члена ряда от его номера.

Пример 1. Найти общий член ряда .

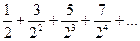Решение. Последовательные числители образуют арифметическую прогрессии. 1,3,5,7,…; й член прогрессии находим по формуле Здесь , поэтому . Последовательные знаменатели образуют геометрическую прогрессии. -й член этой прогрессии . Следовательно, общий член ряда

Пример 2. Найти общий член ряда

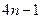Решение. Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель степени го члена равен . Числители дробей 2/3,3/7,4/11,5/15,… образуют арифметическую прогрессию с первым членом 2 и разностью 1. Поэтому -й числитель равен . Знаменатели образуют арифметическую прогрессию с первым членом 4 и разностью 4. Следовательно, -й знаменатель равен . Итак, общим членом ряда является

Сумма первых членов ряда называется -й частичной суммойряда. Рассмотрим последовательность частичных сумм числового ряда:

, , , …

Определение. Если существует конечный предел последовательности частичных сумм ряда, то говорят, что числовой ряд сходится. Этот предел называют суммой ряда .

Числовой ряд называют расходящимся, если не существует или .

Пример 1. Рассмотрим ряд 1/2+1/4+1/8+1/16+...+

Сторона квадрата равна единице, следовательно площадь 1/2+1/4+1/16+1/32+…... = 1

Пример 2. Числовой ряд является сходящимся. Это легко доказать, рассмотрев последовательность частичных сумм. Действительно,

, ,

, …,

.

Следовательно, , т.е. ряд сходится.

Пример 3. Найти сумму ряда .

Решение. Разлагаем общий член ряда на простейшие дроби:

Выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда: .

Составляем ю частичную сумму ряда: 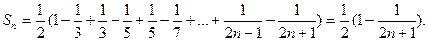Вычисляем сумму ряда по формуле , получаем . Ряд сходится и его сумма равна 1/2.

Пример 4. Найти сумму ряда .

Решение. Разложим общий член ряда на простейшие дроби с помощью метода неопределенных коэффициентов:

. Умножая на знаменатель левой части, придем к тождеству

Полагая последовательно находим: при : 1=2A; A=1/2; при : при 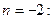Таким образом, , т.е. . Выписываем несколько членов ряда, чтобы было видно, какие слагаемые сокращаются при вычислении частичной суммы ряда:

.

Составляем ю частичную сумму ряда и сокращаем все слагаемые, какие возможно:

Вычисляем сумму ряда по формуле , получаем .

Числовой ряд расходится, так как последовательность частичных сумм не имеет предела.

Известным числовым рядом является геометрическая прогрессия:

Сумма первых членов прогрессии находится по формуле , . Предел этой суммы равен:

,

если , так как . Если , то , поэтому , ряд расходится. Если , то ряд принимает вид . Последовательность частичных сумм расходится, , следовательно, расходится и ряд. При ряд принимает вид - в этом случае при четном и при нечетном . Следовательно, не существует, а ряд расходится.

Пример 5. Исследовать сходимость ряда .

Решение. Ряд составлен из членов бесконечно убывающей геометрической прогрессии и поэтому сходится. Найдем сумму ряда. Здесь (знаменатель прогрессии) Следовательно,