Свойства сходящихся рядов

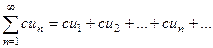Теорема 1. Если все члены сходящегося ряда умножить на число , то ряд так же сходится и его сумма равна . Если же ряд расходится и , то и ряд расходится.

Доказательство. Обозначим -ю частичную сумму ряда через . Тогда

.

Следовательно, , т.е. ряд сходится и имеет сумму .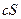

Покажем теперь, что если ряд расходится, а число , то и ряд расходится. Допустим противоположное, что ряд сходится и имеет сумму . Тогда .

Отсюда получаем: , т.е. ряд сходится, что противоречит условию.

Теорема 2. Если сходится ряд и сходится ряд , а их суммы равны и соответственно, то сходятся и ряды , (), причем сумма каждого равна соответственно .

Доказательство. Обозначим -е частные суммы рядов , , и , через , и соответственно. Тогда

,

т.е. каждый из рядов сходится, и сумма его равна соответственно.

Теорема 3. Если сходится ряд , то сходится и любой ряд, полученный из данного перегруппировкой его членов.

Теорема 4. Если сходится ряд, полученный из исходного ряда отбрасыванием конечного числа членов, то сходится и исходный ряд, а если сходится числовой ряд , то сходятся и ряд, полученный отбрасыванием конечного числа членов.

Доказательство. Сумму первых отброшенных членов обозначим . Оставшиеся члены ряда называются -м остатком ряда. Рассмотрим последовательность частичных сумм оставшихся членов : , , , …. Данная последовательность по условию теоремы является сходящейся, т.е. является некоторым числом . Рассмотрим последовательность частичных сумм исходного ряда , которая является сходящейся, т.к. . Это и означает, что исходный числовой ряд тоже сходится. Вторая часть теоремы доказывается с помощью аналогичных рассуждений.

Пример 6. Исследовать сходимость ряда .

Решение. Данный ряд получен из гармонического

отбрасыванием первых десяти членов. Следовательно, он

расходится.

Ряд, полученный из данного отбрасыванием конечного числа членов называют -м остатком исходного ряда и обозначают .

Теорема 5. Для того, чтобы ряд был сходящимся, необходимо и достаточно, чтобы .

Доказательство. Так как , где - частичная сумма ряда, то переходя к пределу, получаем:

Необходимый признак сходимости числового ряда.

Нахождение - й частичной суммы и ее предела не удобно для практического использования. Поэтому для выяснения сходимости ряда устанавливают необходимые и достаточные признаки сходимости. Рассмотрим необходимый признак сходимости.

Теорема(необходимый признак сходимости). Если числовой ряд сходится, то его общий член стремится к нулю, т.е. .

Доказательство. Пусть числовой ряд сходится и . Тогда и (при и () ). Поскольку при , получаем: .

Следствие. Если , т.е. необходимое условие сходимости числового ряда не выполняется, то ряд расходится.

Пример 7. Исследовать сходимость ряда .

Решение: Ряд расходится, т.к.

,

т.е. выполняется достаточное условие расходимости ряда.

Пример 8. Исследовать сходимость ряда

Решение: Данный ряд расходится, т.к. .

Необходимый признак сходимости числового ряда не является достаточным: из условия не следует что, ряд сходится. Существует множество расходящихся числовых рядов, для которых . Например, рассмотрим гармонический ряд

.

Очевидно, что . Однако гармонический ряд расходится. Докажем расходимость гармонического ряда:

(1)

(2)

Очевидно сумма ряда (2) больше, чем ряда (1). Ряд (2) расходится, так как , значит, и гармонический ряд является расходящимся.

1.22. Достаточные признаки сходимости числовых рядов.

Сходимость и расходимость числовых рядов с положительными членами можно установить с помощью сравнения его с другим («эталонным») рядом, о котором заранее известно, сходится он или расходится. Такое сравнение производится на основе двух теорем сравнения.

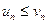Теорема 1. Пусть даны два знакоположительных ряда и . Если для всех выполняется неравенство , то из сходимости ряда следует сходимость ряда , из расходимости ряда следует расходимость ряда .

Доказательство. Обозначим -e частичные суммы рядов и соответственно через и . Суммируя неравенства 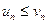получаем, что .

Пусть ряд сходится и . Члены ряда положительны, поэтому . Используя неравенство , получаем . Последовательность монотонно возрастает, поскольку >0, и ограничена сверху числом , следовательно, имеет предел , т. е. ряд сходится.

Пусть теперь знакоположительный числовой ряд расходится: . Тогда, с учетом неравенства получаем , т. е. ряд расходится.

Теорема 1 имеет место и в том случае, когда неравенство 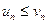выполняется не для всех членов рядов и , а начиная с некоторого номера.

Пример 9. Исследовать на сходимость ряд .

Решение: Сравним данный ряд с рядом геометрической прогрессии , о котором заранее известно, что он сходится, так как является бесконечно убывающей геометрической прогрессией. Поскольку для любого выполняется неравенство , то из сходимости геометрической прогрессии следует и сходимость ряда . Следовательно, данный ряд сходится.

Пример 10. Исследовать сходимость ряда

Решение. Так как , то необходимое условие сходимости ряда выполнено. Применим первый признак сравнения. Поскольку , имеем и, следовательно, . Так как ряд расходится как обобщенный гармонический ряд с , то по первому признаку сравнения расходится и исходный ряд.

Теорема 2. Пусть даны два знакоположительных ряда и . Если существует конечный, предел , то ряды и сходятся или расходятся одновременно.

Доказательство. Пусть существует конечный предел, тогда

или

, .

Если ряд сходится, то из левого неравенства и первой теоремы сравнения следует, что и ряд тоже сходится. Если ряд расходится, то из правого неравенства и первой теоремы сравнения вытекает, что и ряд тоже расходится. Аналогично, если известна сходимость или расходимость ряда можно сделать вывод о поведении

ряда

Пример 11. Исследовать сходимость ряда .

Решение. Здесь 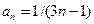. Сравним ряд с гармоническим рядом, у которого : . Следовательно, данный ряд расходится по второму признаку сравнения.

Пример 12. Исследовать сходимость ряда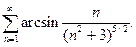

Решение. Так как , то необходимое условие сходимости ряда выполнено. Проверяем, что члены данного ряда положительны. Действительно, 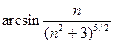>0 при всех , так как . Имеем при Ряд сходится как обобщенный гармонический ряд с . Следовательно, в силу второго признака сравнения исходный ряд также сходится.

Пример 14. Исследовать сходимость ряда

Решение. Поскольку при , упрощаем выражение для : т. е. будем исследовать сходимость ряда и затем воспользуемся вторым признаком сравнения. Поскольку , вычисляем , учитывая, что : . Так как , то ряд сходится. Следовательно, по второму признаку сравнения сходится и исходный ряд.

Пример 15. Исследовать сходимость ряда .

Решение: Здесь . В качестве эталонного ряда сравнения возьмем расходящийся гармонический ряд с общим членом . Имеем . Следовательно, исходный ряд расходится.