Определение положения точки  с помощью декартовых координат не является единственным способом.
с помощью декартовых координат не является единственным способом.
Пусть дана некоторая плоскость. Выберем на ней точку  , из нее проведем луч
, из нее проведем луч  . На этом луче выберем единицу масштаба. Тогда любая точка
. На этом луче выберем единицу масштаба. Тогда любая точка  плоскости будет однозначно определена, если известно ее расстояние
плоскости будет однозначно определена, если известно ее расстояние  от точки
от точки  , то есть длина отрезка
, то есть длина отрезка  , и угол
, и угол  , образованный лучом
, образованный лучом  и отрезком
и отрезком  . Пара чисел
. Пара чисел  и
и  называется полярными координатами точки
называется полярными координатами точки  :
:  – полярный угол,
– полярный угол,  – полярный радиус, луч
– полярный радиус, луч  – полярная ось, точка
– полярная ось, точка  – полюс.
– полюс.
Угол φ считается положительным, если он отсчитывается от полярной оси в направлении, противоположном направлению часовой стрелки. Область изменения полярных координат определяется системой неравенств:  .
.
Если полюс полярной системы координат совместить с началом некоторой декартовой системы, заданной на той же плоскости, а полярную ось направить по оси  , то полярные координаты
, то полярные координаты 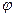 и
и  некоторой точки
некоторой точки  будут связаны с декартовыми координатами
будут связаны с декартовыми координатами  и
и  следующими соотношениями:
следующими соотношениями: 
Если известны полярные координаты 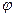 и
и  , то декартовы координаты
, то декартовы координаты  и
и  точки
точки  вычисляются по формулам:
вычисляются по формулам:
 .
.
Пример 12. Найти полярные координаты точки  , если полюс совпадает с началом координат, а полярная ось - с положительным направлением оси абсцисс.
, если полюс совпадает с началом координат, а полярная ось - с положительным направлением оси абсцисс.
Решение.
Имеем 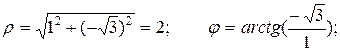
угол 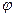 находится в четвертой четверти, то есть
находится в четвертой четверти, то есть
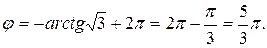
Ответ:  .
.
Решение типового варианта
Задача 1. Даны координаты вершин треугольника  :
:  ,
, 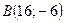 ,
,  . Найти: 1) длину стороны
. Найти: 1) длину стороны  ; 2) уравнения сторон
; 2) уравнения сторон  и
и 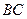 и их угловые коэффициенты; 3) угол
и их угловые коэффициенты; 3) угол  в радианах с точностью до двух знаков; 4) уравнение высоты
в радианах с точностью до двух знаков; 4) уравнение высоты  и ее длину; 5) уравнение медианы
и ее длину; 5) уравнение медианы  и координаты точки
и координаты точки  пересечения этой медианы с высотой
пересечения этой медианы с высотой  ; 6) уравнение прямой, проходящей через точку
; 6) уравнение прямой, проходящей через точку  параллельно стороне
параллельно стороне  ; 7) координаты точки
; 7) координаты точки  , расположенной симметрично точке
, расположенной симметрично точке  относительно прямой
относительно прямой  .
.
Решение.
1.Расстояние  между точками
между точками  и
и  определяется по формуле
определяется по формуле
 (1)
(1)
Применяя (1), находим длину стороны  :
:  .
.
2. Уравнение прямой, проходящей через точки  и
и  , имеет вид
, имеет вид
 (2)
(2)
Подставляя в (2) координаты точек  и
и  , получим уравнение стороны
, получим уравнение стороны  :
:  ;
; 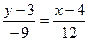 ;
;  ;
;  ;
;

 .
.
Решив последнее уравнение относительно  , находим уравнение стороны
, находим уравнение стороны  в виде уравнения прямой с угловым коэффициентом:
в виде уравнения прямой с угловым коэффициентом:
 ;
;  , откуда
, откуда  .
.
Подставив в (2) координаты точек  и
и  , получим уравнение прямой
, получим уравнение прямой 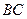 :
:


 ;
;  ;
;  ;
;

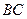 , откуда
, откуда  .
.
3. Известно, что тангенс угла 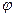 между двумя прямыми, угловые коэффициенты которых соответственно равны
между двумя прямыми, угловые коэффициенты которых соответственно равны  , вычисляется по формуле
, вычисляется по формуле
 (3)
(3)
Искомый угол  образован прямыми
образован прямыми  и
и 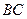 , угловые коэффициенты которых найдены:
, угловые коэффициенты которых найдены:  ;
; 
 Применяя (3), получим
Применяя (3), получим
 ;
;
 , или
, или  рад
рад  рад.
рад.
4. Уравнение прямой проходящей через данную точку в заданном направлении, имеет вид  (4)
(4)
Высота  перпендикулярна стороне
перпендикулярна стороне  . Чтобы найти угловой коэффициент высоты
. Чтобы найти угловой коэффициент высоты  , воспользуемся условием перпендикулярность прямых. Так как
, воспользуемся условием перпендикулярность прямых. Так как  , то
, то  . Подставив в (4) координаты точки
. Подставив в (4) координаты точки  и найденный угловой коэффициент высоты, получим
и найденный угловой коэффициент высоты, получим
 ;
;  ;
; 
 .
.
Чтобы найти длину высоты  , определим сперва координаты точки
, определим сперва координаты точки  – точки пересечения прямых
– точки пересечения прямых  и
и  . Решая совместно систему
. Решая совместно систему  находим
находим  , т.е.
, т.е.  .
.
По формуле (1) находим длину высоты  :
:  .
.
5. Чтобы найти уравнение медианы  , определим сначала координаты точки
, определим сначала координаты точки  , которая является серединой стороны
, которая является серединой стороны 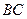 , применяя формулы деления отрезка на две равные части:
, применяя формулы деления отрезка на две равные части:
 (5)
(5)
Следовательно, 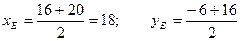 ;
;  .
.
Подставив в (2) координаты точек  и
и  , находим уравнение медианы:
, находим уравнение медианы:  ;
;  ;
;  .
. 
Чтобы найти координаты точки пересечения высоты  и медианы
и медианы  , решим совместно систему уравнений
, решим совместно систему уравнений 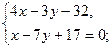
 ,
,  ;
;  .
.
6. Так как искомая прямая параллельна стороне  , то ее угловой коэффициент будет равен угловому коэффициенту прямой
, то ее угловой коэффициент будет равен угловому коэффициенту прямой  . Подставив в (4) координаты найденной точки
. Подставив в (4) координаты найденной точки  и угловой коэффициент
и угловой коэффициент  , получим
, получим  ;
;  ;
; 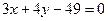

 .
.
7. Так как прямая  перпендикулярна прямой
перпендикулярна прямой  , то искомая точка
, то искомая точка  , расположенная симметрично точке
, расположенная симметрично точке  относительно прямой
относительно прямой  , лежит на прямой
, лежит на прямой  . Кроме того, точка
. Кроме того, точка  является серединой отрезка
является серединой отрезка  . Применяя формулы (5), находим координаты искомой точки
. Применяя формулы (5), находим координаты искомой точки  :
:
 ;
;  ;
;  ;
;  ;
;  .
.
Треугольник  , высота
, высота  , медиана
, медиана  , прямая
, прямая  и точка
и точка  построены в системе координат
построены в системе координат  на рис. 6.
на рис. 6.

Рис.6
Задача 2. Даны координаты четырех точек:  ,
,  ,
, 
С (3; 2; 0) и  . Требуется: 1) составить уравнение плоскости
. Требуется: 1) составить уравнение плоскости 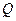 , проходящей через точки
, проходящей через точки  ,
,  и
и  ; 2) составить каноническое уравнение прямой, проходящей через точку
; 2) составить каноническое уравнение прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 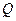 ; 3) найти точки пересечения полученной прямой с плоскостью
; 3) найти точки пересечения полученной прямой с плоскостью 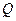 и с координатными плоскостями
и с координатными плоскостями  ,
,  и
и  ; 4) найти расстояние от точки
; 4) найти расстояние от точки  до плоскости
до плоскости 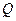 .
.
Решение.
1. Уравнение плоскости, проходящей через три данные точки  ,
,  ,
,  , имеет вид
, имеет вид  (1)
(1)
Подставив в (1) координаты точек  ,
,  и
и  , получим:
, получим:


Разложим определитель по элементам первой строки:
 .
.
Сократив на 5, получим уравнение искомой плоскости 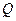 :
:
 (2)
(2)
2. Канонические уравнения прямой в пространстве имеют вид  ; (3)
; (3)
где  - координаты точки, через которую проходит прямая (3), а
- координаты точки, через которую проходит прямая (3), а  - координаты направляющего вектора этой прямой. По условию прямая проходит через точку
- координаты направляющего вектора этой прямой. По условию прямая проходит через точку  и перпендикулярна плоскости
и перпендикулярна плоскости 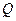 . Следовательно, подставив в (3) координаты точки
. Следовательно, подставив в (3) координаты точки  и заменив числа
и заменив числа  соответственно числами 2; –1; –2 [коэффициенты общего уравнения плоскости (2)], получим
соответственно числами 2; –1; –2 [коэффициенты общего уравнения плоскости (2)], получим
 . (4)
. (4)
3. Чтобы найти точки пересечения прямой (4) с плоскостью (2), запишем сначала уравнение прямой (4) в параметрическом виде.
Пусть  , где t – некоторый параметр. Тогда уравнение прямой можно записать так:
, где t – некоторый параметр. Тогда уравнение прямой можно записать так:
 . (5)
. (5)
Подставив (5) в(2), получим значение параметра t:
 ;
;  ;
;  ;
;  .
.
Подставим в (5)  , находим координаты точки
, находим координаты точки  пересечения прямой (4) с плоскостью (2):
пересечения прямой (4) с плоскостью (2):  ;
; 
Пусть  – точка пересечения прямой (4) с координатной плоскостью
– точка пересечения прямой (4) с координатной плоскостью  ; уравнение этой плоскости
; уравнение этой плоскости  .
.
При  из (5) получаем
из (5) получаем 
 .
.
Пусть  – точка пересечения прямой (4) с плоскостью
– точка пересечения прямой (4) с плоскостью  ; уравнение этой плоскости
; уравнение этой плоскости  .
.
При  из (5) получаем
из (5) получаем  ;
; 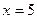 ;
;  ;
;  .
.
Пусть  – точка пересечения прямой (4) с плоскостью
– точка пересечения прямой (4) с плоскостью  .
.
Уравнение этой плоскости  .
.
При  из (5) получаем
из (5) получаем  ;
;  .
.
4. Так как точка  лежит на прямой (4), которая перпендикулярна плоскости
лежит на прямой (4), которая перпендикулярна плоскости 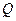 и пересекается с ней в точке
и пересекается с ней в точке  , то для нахождения расстояния от точки
, то для нахождения расстояния от точки  до плоскости
до плоскости 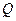 достаточно найти расстояние между точками
достаточно найти расстояние между точками  и
и  :
:  .
.
Задача 3. Даны вершины пирамиды  ,
,  ,
, 
 . Найти 1)угол между ребрами
. Найти 1)угол между ребрами  и
и  ; 2) уравнение плоскости
; 2) уравнение плоскости  ; 3) уравнение и высоты, опущенной из вершины
; 3) уравнение и высоты, опущенной из вершины  на грань
на грань  ; 4) угол между ребром
; 4) угол между ребром  и гранью
и гранью  ; 5) площадь грани
; 5) площадь грани  ; 6)объем пирамиды
; 6)объем пирамиды  .
.
Решение.
1) Угол между ребрами  и
и  найдем, как угол между векторами. Выразим из формулы
найдем, как угол между векторами. Выразим из формулы 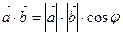
 =
= 
Вычислим координаты вектора  и
и  :
:
 =
=  =
=  ;
;  =
=  =
= 
 =
=  ;
;
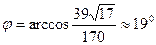
2) Уравнение плоскости  найдем из равенства:
найдем из равенства:

 ;
;  ;
; 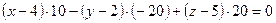 ;
;

 .
.
3) Уравнение высоты  , опущенной из вершины
, опущенной из вершины  на грань
на грань 
 , составим по точке
, составим по точке  и направляющему вектору
и направляющему вектору 
 плоскости
плоскости  . Каноническое уравнение
. Каноническое уравнение  примет вид:
примет вид:


4) Вычислим координаты вектора  :
:
 .
.
Угол  между ребром
между ребром  и гранью
и гранью  является дополнительным углом для угла
является дополнительным углом для угла 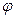 , образованного перпендикуляром, проведенным к плоскости треугольника
, образованного перпендикуляром, проведенным к плоскости треугольника  и ребром
и ребром  .
.  . Для нахождения
. Для нахождения  вычислим координаты векторного произведения векторов
вычислим координаты векторного произведения векторов  и
и  :
:
 ;
;
 .
.
 .
.
 ;
;
 ;
;  .
.
5) Площадь грани  равна половине площади параллелограмма, построенного на сторонах
равна половине площади параллелограмма, построенного на сторонах  и
и  , т.е.
, т.е.
 .
.
6)Объем пирамиды равен одной шестой от объема параллелепипеда, построенного на ребрах  ,
,  и
и  . Следовательно
. Следовательно
 .
.
Ответ:  ;
; 
 ;
;  ;
;  .
.
Задача 4. Привести уравнение к каноническому виду и построить график.
а)  ; б)
; б)  ; в)
; в) 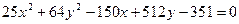 .
.
Решение а) 
1. Группируем  и
и 

2. Выносим коэффициент при  за скобку
за скобку 
3. В скобках выделяем полный квадрат


4. Раскрываем внешние скобки 
5. Квадрат оставляем слева, а все остальное переносим вправо

6. Выносим коэффициент при  за скобку
за скобку 
7. Делим обе части равенства на 2 
Полученное уравнение определяет параболу с вершиной в т. 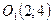 . Ветви параболы направлены вправо.
. Ветви параболы направлены вправо.
Строим график.
В системе координат  отмечаем точку
отмечаем точку 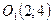 и через нее проводим новые оси
и через нее проводим новые оси  . Ось
. Ось  будет осью симметрии параболы. Найдем точки пересечения параболы с осями координат.
будет осью симметрии параболы. Найдем точки пересечения параболы с осями координат.
С осью  :
: 
 ;
;  ;
;  .
.
 . Отмечаем ее в системе
. Отмечаем ее в системе  .
.
С осью  :
: 
 ;
;  ;
;
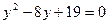
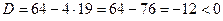 Точек пересечения с осью
Точек пересечения с осью  нет.
нет.
Строим точку  симметричную точке
симметричную точке  относительно оси
относительно оси  . Через точки
. Через точки  проводим параболу.
проводим параболу.

Решение б) 
1. Группируем  и
и 

2. Выносим коэффициент при  и
и  за скобки
за скобки

3. В каждой скобке выделяем полный квадрат
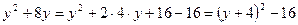


4. Раскрываем внешние скобки

5. Квадраты оставляем слева, а все остальное переносим вправо

6. Делим обе части равенства на 36


Полученное уравнение определяет гиперболу с центром в точке  . Ветви гиперболы направлены вправо-влево.
. Ветви гиперболы направлены вправо-влево.
Действительная полуось  , мнимая полуось
, мнимая полуось 
Фокусы расположены на оси  .
.
Строим график.
1. В системе координат  отмечаем точку
отмечаем точку  и через нее проводим новые оси
и через нее проводим новые оси  .
.
2. В системе координат  от точки
от точки  откладываем вправо и влево действительную полуось
откладываем вправо и влево действительную полуось  . Получаем точки
. Получаем точки  и
и  . Вверх и вниз откладываем мнимую полуось
. Вверх и вниз откладываем мнимую полуось  . Получаем точки
. Получаем точки  и
и  .
.
3. Через точки  ,
,  ,
,  ,
,  проводим прямые, параллельные координатным осям. Получаем прямоугольник.
проводим прямые, параллельные координатным осям. Получаем прямоугольник.
4. В прямоугольнике проводим диагонали и продолжаем их за прямоугольник. Эти прямые являются асимптотами гиперболы.
5. Из точек  и
и  проводим ветви гиперболы, приближая их к асимптотам.
проводим ветви гиперболы, приближая их к асимптотам.

Решение в) 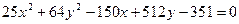
1. Группируем  и
и 

2. Выносим коэффициент при  и
и  за скобки
за скобки

3. В каждой скобке выделяем полный квадрат
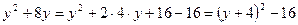

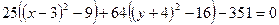
4. Раскрываем внешние скобки

5. Квадраты оставляем слева, а все остальное переносим вправо
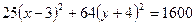
6. Делим обе части равенства на 1600


7. Полученное уравнение определяет эллипс с центром в точке 
и полуосями  и
и 
Строим график.
1. В системе координат  отмечаем точку
отмечаем точку  и через нее проводим новые оси
и через нее проводим новые оси  .
.
2. В системе координат  от точки
от точки  откладываем вправо и влево полуось
откладываем вправо и влево полуось  . Получаем точки
. Получаем точки  и
и  . Вверх и вниз откладываем полуось
. Вверх и вниз откладываем полуось  . Получаем точки
. Получаем точки  и
и  .
.
3. Через точки  ,
,  ,
,  ,
,  проводим прямые, параллельные координатным осям. Получаем прямоугольник.
проводим прямые, параллельные координатным осям. Получаем прямоугольник.
4. Внутри прямоугольника строим эллипс.

Задача 5. Линия задана уравнением  в полярной системе координат. Требуется:
в полярной системе координат. Требуется:
1) найти уравнения данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
2) по полученному уравнению определить, какая это линия;
3) построить линию.

Решение.
1) Изменяя значения угла от 0 до 2π через промежуток  , зададим таблицу.
, зададим таблицу.
| φ |  |  |  |  |  | 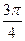 |  |  |  |  |  |  | |
| r | 3,3(3) | 3,42 | 3,69 | 4,197 | 6,18 | 7,73 | 9,29 | 9,29 | 7,73 | 6,18 |
| φ | 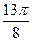 |  | 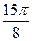 |  |
| r | 4,197 | 3,69 | 3,42 | 3,3(3) |

2) Полярные и декартовы системы координат взаимно связаны формулами:
 ;
;  ;
;  ;
;
Следовательно:  ;
;  .
.
 умножим обе части равенства на
умножим обе части равенства на 
 ;
; 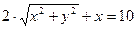 ;
; 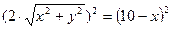 ;
;
 ;
;  ;
;
 - уравнение задает эллипс.
- уравнение задает эллипс.
Приведём его к каноническому виду:
 ;
;
 ;
;
 ;
;
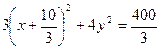 разделим обе части равенства на
разделим обе части равенства на 
 .
.
Следовательно, данное уравнение задаёт эллипс с центром в точке с координатами  полуосями
полуосями  ,
,  .
.
Варианты РГР
Задание 1
Даны координаты вершин треугольника  .
.
Найти: 1) длину стороны  ; 2)уравнения сторон
; 2)уравнения сторон  и
и 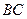 и их угловые коэффициенты; 3)угол
и их угловые коэффициенты; 3)угол  в радианах с точностью до двух знаков; 4) уравнение высоты
в радианах с точностью до двух знаков; 4) уравнение высоты  и ее длину; 5) уравнение медианы
и ее длину; 5) уравнение медианы  и координаты точки
и координаты точки  пересечения этой медианы с высотой
пересечения этой медианы с высотой  ; 6) уравнение прямой, проходящей через точку
; 6) уравнение прямой, проходящей через точку  параллельно стороне
параллельно стороне  ; 7) координаты точки
; 7) координаты точки  , расположенной симметрично точке
, расположенной симметрично точке  относительно прямой
относительно прямой  .
.
| Номер варианта | Координаты  | Координаты  | Координаты  |
| (-8;-3) | (4;-12) | (8;10) | |
| (-5;7) | (7;-2) | (11;20) | |
| (-12;-1) | (0;-10) | (4;12) | |
| (-10;9) | (2;0) | (6;22) | |
| (0;2) | (12;-7) | (16;15) | |
| (-9;6) | (3;-3) | (7;19) | |
| (1;0) | (13;-9) | (17;13) | |
| (-4;10) | (8;1) | (12;23) | |
| (2;5) | (14;-4) | (18;18) | |
| (-1;4) | (11;-5) | (15;17) | |
| (-2;7) | (10;-2) | (8;12) | |
| (-6;8) | (6;-1) | (4;13) | |
| (3;6) | (15;-3) | (13;11) | |
| (-10;5) | (2;-4) | (0;10) | |
| (-4;12) | (8;3) | (6;17) | |
| (-3;10) | (9;1) | (7;15) | |
| (4;1) | (16;-8) | (14;6) | |
| (-7;4) | (5;-5) | (3;9) | |
| (0;3) | (12;-6) | (10;8) | |
| (-5;9) | (7;0) | (5;14) | |
| (-3;-2) | (-4;2) | (5;0) | |
| (2;-2) | (-3;0) | (0;-2) | |
| (5;4) | (-1;-2) | (3;-2) | |
| (3;6) | (0;2) | (1;-2) | |
| (1;-4) | (4;4) | (-1;2) | |
| (4;6) | (7;2) | (-2;0) | |
| (0;6) | (8;2) | (2;6) | |
| (-2;4) | (0;-6) | (4;2) | |
| (-4;-2) | (1;8) | (0;4) | |
| (3;4) | (2;-4) | (5;6) |
Заданий 2
Даны координаты точек  ,
,  ,
,  и
и 
Найти: 1) уравнение плоскости 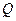 , проходящей через точки
, проходящей через точки  ,
,  и
и  ; 2) канонические уравнения прямой, проходящей через точку
; 2) канонические уравнения прямой, проходящей через точку  перпендикулярно плоскости
перпендикулярно плоскости 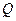 ; 3)точки пересечения полученной с плоскостью
; 3)точки пересечения полученной с плоскостью 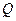 и с координатными плоскостями
и с координатными плоскостями  ,
,  ,
,  ; 4) расстояние от точки
; 4) расстояние от точки  до плоскости
до плоскости 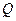 .
.
| Номер варианта | Координаты А | Координаты В | Координаты С | Координаты  | |
| (-3;-2;-4) | (-4;2;-7) | (5;0;3) | (-1;3;0) | ||
| (2;-2;1) | (-3;0;-5) | (0;-2;-1) | (-3;4;2) | ||
| (5;4;1) | (-1;-2;-2) | (3;-2;2) | (-5;5;4) | ||
| (3;6;-2) | (0;2;-3) | (1;-2;0) | (-7;6;6) | ||
| (1;-4;1) | (4;4;0) | (-1;2;-4) | (-9;7;8) | ||
| (4;6;-1) | (7;2;4) | (-2;0;-4) | (3;1;-4) | ||
| (0;6;-5) | (8;2;5) | (2;6;-3) | (5;0;-6) | ||
| (-2;4;-6) | (0;-6;1) | (4;2;1) | (7;-1;-8) | ||
| (-4;-2;-5) | (1;8;-5) | (0;4;-4) | (9;-2;-10) | ||
| (3;4;-1) | (2;-4;2) | (5;6;0) | (11;-3;-12) | ||
| (2;-3;1) | (6;1;-1) | (4;8;-9) | (2;-1;2) | ||
| (5;-1;-4) | (9;3;-6) | (7;10;-14) | (5;1;-3) | ||
| (1;-4;0) | (5;0;-2) | (3;7;-10) | (1;-2;1) | ||
| (-3;-6;2) | (1;-2;0) | (-1;5;-8) | (-3;-4;3) | ||
| (-1;1;-5) | (3;5;-7) | (1;12;-15) | (-1;3;-4) | ||
| (-4;2;-1) | (0;6;-3) | (-2;13;-11) | (-4;4;0) | ||
| (0;4;3) | (4;8;1) | (2;15;-7) | (0;6;4) | ||
| (-2;0;-2) | (2;4;-4) | (0;11;-12) | (-2;2;-1) | ||
| (3;3;-3) | (7;7;-5) | (5;14;-13) | (3;5;-2) | ||
| (4;-2;5) | (8;2;3) | (6;9;-5) | (4;0;6) | ||
| (-5;0;1) | (-4;-2;3) | (6;2;11) | (3;4;9) | ||
| (1;-4;0) | (2;-6;2) | (12;-2;10) | (9;0;8) | ||
| (-1;-2;-8) | (0;-4;-6) | (10;0;2) | (7;2;0) | ||
| (0;2;-10) | (1;0;-8) | (11;4;0) | (8;6;-2) | ||
| (3;1;-2) | (4;-1;0) | (14;3;8) | (11;5;6) | ||
| (-8;3;-1) | (-7;1;1) | (3;5;9) | (0;7;7) | ||
| (2;-1;-4) | (3;-3;-2) | (13;1;6) | (10;3;4) | ||
| (-4;5;-5) | (-3;3;-3) | (7;7;5) | (4;9;3) | ||
| (-2;-3;2) | (-1;-5;4) | (9;-1;12) | (6;1;10) |
|
|
Подборка статей по вашей теме:
- Системы координат. – делятся на плановые и высотные
- Полярные координаты
- Частотные характеристики звеньев и систем автоматического регулирования
- Спутниковые радионавигационные системы первого поколения
- Двойной интеграл в полярной системе координат
- Системы координат в геодезии. Государственные геодезические и нивелирные сети
- Понятие географических, прямоугольных и полярных координат
- Системы координат, применяемые в топографии. Определение координат объектов на земной поверхности
- Системы SCАDA
- Скорость и ускорение точки в цилиндрических координатах
 2015-10-22
2015-10-22 3485
3485