Структурная организация сложных автоматов

В информационных системах реального времени предельное быстродействие достигается за счет аппаратной реализации устройств управления, которые могут составлять до 50 % оборудования.

Сложность организации самих автоматов определяется количеством состояний автомата и числом q логических условий { }. Структура автомата Мура, представленная на рис. 92, определяется уравнениями:

; , (9)

где: – выходные сигналы (микрооперации) управления операционным устройством (ОУ).

Система булевых функций есть набор схем «ИЛИ», объединяющих разные выходы от дешифратора кода разрядностью m в команды . Реализация системы булевых функций не представляет затруднений, как и реализация остальных блоков автомата, кроме ОУ, который не относится непосредственно к автомату.

Наибольшую сложность реализации представляет система булевых функций , число переменных на входе которой определяется конкатенацией кода в виде и кортежа логических условий *.

Реализация обеспечивается с помощью ПЗУ (ПЛМ) объемом . Например, уже при m = 5, q = 11, m + q = 16 величина бит. Но разрядность типовых ПЗУ (ПЛМ) на выходе равна 4, 8, поэтому реальное 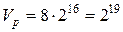бит = 0,5 Мб.

В относительно медленнодействующих системах управления мехатроникой и технологическими процессами переходят к программной реализации автоматов по абстрактной модели (9) со снижением быстродействия на 2–3 порядка по сравнению с аппаратной реализацией.

Количество разрядов адресной части может быть существенно сокращено при другой структурной организации автомата (рис. 93), где М (9) – мультиплексор, (13) – схема определения и адреса для М (10).

Как видно из сравнения структурных схем автоматов рис. 92 и 93, к памяти автомата добавляется двойной (10, 12) двухразрядный регистр со схемами «И» (11) для парафазной передачи .

Абстрактная модель такого автомата задается уравнениями (10):

, (2)

Рис. 92. Блок-схема автомата управления

Рис. 93. Блок-схема автомата управления с выбором логического условия

Рис. 94. Алгоритм управления

Рис. 95. Граф переходов классического автомата

Рис. 96. Преобразованный алгоритм управления

Рис. 97. Граф переходов автомата с выбором логического условия

Схема рис. 93 получается как следствие нового метода синтеза автомата, основанного на преобразовании граф-схемы (ГСА) автомата.

Преобразуем исходную ГСА (рис. 94) таким образом, чтобы после каждого логического оператора как по ветви , так и по ветви следующим всегда был один из операторов , но не . Такое преобразование осуществляется введением пустых операторов для выполнения вышеназванного условия (рис. 96). Рис. 96 в этом случае будет соответствовать и другой граф переходов. Как видно из графа рис. 97 (в отличие от рис. 95), теперь из каждого состояния возможен только один (безусловный переход) или два выхода по условию или . Других вариантов нет, не может быть трех и более выходов из (табл. 36).

Таблица 36

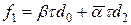
Отсюда можно сделать вывод, что для определения кода достаточно только кода и двух дополнительных разрядов для представления наличия безусловного перехода и значения или . Правильность переходов ® будет однозначна тогда, когда каждому будет соответствовать определенное из множества . Это условие можно выполнить реализацией булевой функции от кода . Фактически после преобразования получается ГСА с одним-единственным условием . Поскольку может принимать значения «0» и «1», то следует его нулевое значение отличать от безусловного перехода, для чего необходимо второе условие . Тогда независимо от числа логических условий (q) количество переменных для (2) определится величиной m + 2.

Схема СС(1) в схеме рис. 93 должна работать за три такта:

– опрос (2) с записью на Рг и опрос (13) с записью на Рг адреса М(9);

– опрос мультиплексора М(9) с записью на Рг(10);

– перепись конкатенации на регистры 5, 12.

Переход к синхронизации тремя импульсами вместо двух () практически не приведет к снижению быстродействия, т.к. << Т. Здесь Т – период следования импульсов синхронизации.

Как видно из анализа, новое значение функций переходов в автомате позволит существенно упростить реализацию схемы (2) за счет введения мультиплексора и весьма простой схемы (13) с дополнительным тактом синхронизации. Такое упрощение стало возможным за счет преобразований ГСА и получения нового типа графов переходов с преобразователем кода в адрес мультиплексора и значение (табл. 37).

Преобразователь может быть выполнен так, что нулевой адрес () всегда будет соответствовать значению , т.е. β = 1, если Здесь Z_r…Z₂Z₁ – код адреса α_j, j = 1, 2,…, q.

Таблица 37

Код			Код адреса
		-
		-
		-
		-
		-
		-
	N

После минимизации по картам Карно для примера получим:

;

;

Для данного конкретного примера ГСА (рис. 94, 95) все операторы различны, поэтому в схеме нет необходимости.

Преимущества новой модели автомата наиболее существенны для сложных автоматов с большим числом состояний ( ³ 32) и логических условий (q ³ 12), причем чем большее число логических условий используется в автомате, тем более эффективна реализация автомата по такой схеме.

Сравнение затрат на комбинационные схемы (табл. 38) проведем для двух вариантов МПА:

а) m = 4 q = 8 m + q = 12 m + 2 = 6

б) m = 5 q = 12 m + q = 17 m + 2 = 7

В табл. 38 затраты на и мультиплексор М определены следующим образом: , , поэтому принято .

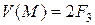Таблица 38

а	m = 4 q = 8 m + q = 12 m +2 = 6 p = 3
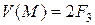
б	m = 5 q = 12 m + q = 17 m +2 = 7 p = 4

Выигрыш в сложности реализации определится коэффициентом К как отношение объема для модели (1) к сумме для модели автомата (2). Для варианта (а) К = 40, для варианта (б) К = 745.

Как видно из табл. 38, в предложенной структуре автомата сложность реализации схемы снижается в десятки и сотни раз.

Приведенные примеры подтверждают эффективность модели (2) даже для простых автоматов (m = 4, q = 8).

В структурной модели обобщенного преобразователя информации функциональная (Ф), информационная (И), адресная (А), логическая (Л) и управляющая подсистемы (У) соответствуют вершинам полного графа.

Для предложенной модели автомата (2) связи подсистем определяются графом рис. 98, при этом аппаратно каждая из подсистем действительно реализуется независимо: Ф – DС (6) и , И – память автомата 3, 4, 5, 11, 12, 13, А – и (13), Л – мультиплексор М (9), У – схема синхронизации СС(1). Поскольку все подсистемы Ф, И, А, Л, У раздельны, то возможна их независимая модификация и оптимизация по тем или иным критериям (надежность, контролепригодность, быстродействие и др.).

Рис. 98. Структурная модель автомата с операционным устройством (ОУ)

Новый метод синтеза для МПА может обеспечить аппаратную реализацию на БИС малой емкости для весьма сложных автоматов [30, 33].

В последнее время из-за трудности аппаратного выполнения сложные автоматы реализуются в виде программной модели для микропроцессоров или контроллеров. Очевидно, что математическая модель автомата по формулам (2) проще модели (1), поэтому и реализуется программным путем за более короткое время и на контроллерах малой разрядности.

Действительно, восьмиразрядный код (m + 2 = 8) контроллера позволяет реализовать автоматы со значением m = 6 практически без ограничений на количество входных логических условий. Автомат с числом состояний и числом логических условий можно отнести к классу не просто сложных, а очень сложных автоматов, реализация которых без специальных приемов декомпозиции затруднена и неэффективна.

Новый метод синтеза дает возможность построения самоконтролируемых автоматов. Более того, в автомате с последовательным выбором логических условий появляется возможность проверки правильности выбора безусловного перехода или логического разветвления дуги в каждом переходе ® . Действительно, в кодах возможны только три комбинации: 00, 10 и 01. Комбинация 11 является запрещенной, так как не может быть выбран одновременно и . Этот дополнительный признак контроля дает возможность более глубокой проверки правильности функционирования автомата.