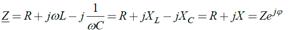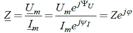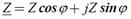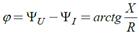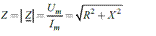Резистор, индуктивность и емкость в цепи соединены последовательно и подключены к источнику эдс е(t)
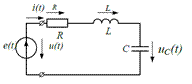Определим полное сопротивление в такой цепи.
| По второму правилу (закону) Кирхгофа:
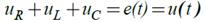В интегро-дифференциальной форме:
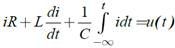Если в цепи действует:
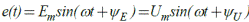Подставив в интегро-дифференциальное уравнение комплексную функцию времени для тока, получим уравнение в символической форме для комплексных амплитуд:
 
| |||||||||||||
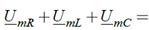
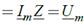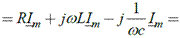
Комплексным сопротивлением цепи называют:
Модуль комплексного сопротивления или полное сопроти вление цепи на переменном токе определяют следующим образом:
Аргумент комплексного сопротивления: Активное сопротивление цепи R является действительной частью комплексного сопротивления, всегда положительно. Реактивное сопротивление цепи X=XL – XC= ωL-(1/ωC) является мнимой частью комплексного сопротивления, может быть положительным или отрицательным. Реактивное сопротивление индуктивности: XL= ωL>0
Реактивное сопротивление емкости: XC=1/ωC>0
| ||||||||||||||
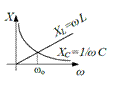
| Зависимость реактивных сопротивлений индуктивности и емкости от частоты. При ω=ωο индуктивное сопротивление становится равным емкостному сопротивление. Реактивное сопротивление цепи в этом случае равно нулю X=0. | |||||||||||||
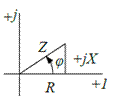
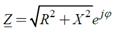|  КС на комплексной плоскости:
Гипотенуза прямоугольного треугольника равна модулю и угол φ треугольника равен аргументу комплексного сопротивления:
 
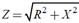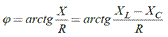Если XL>XC, реактивное сопротивление Х>0 имеет индуктивный характер, то 0о< φ <90о.
Если XL<XC, реактивное сопротивление Х<0 имеет емкостной характер, то -90о< φ <0о.
| |||||||||||||
Комплексное сопротивление цепи
2017-10-25
465Поделись с друзьями:
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
|
|
Сейчас читают про:
6282
5971