Теоретичні відомості про закони розподілу випадкових величин

При випробуваннях нових зразків техніки найбільш достовірну інформацію про надійність її роботи для спостереження та фіксації відмов (порушення працездатності), їх статистичне оброблення та аналіз причин їх виникнення. Зафіксовані відмови, як правило, непередбачувані та мають вигляд випадкових величин. Ймовірнісні методи їх дослідження розвиваються з використанням теоретичних розподілів випадкових величин, які часто називають законами теорії надійності. Розглянемо найбільш уживані теоретичні розподіли.

10.2.1. Нормальний розподіл

Одним із найбільш універсальних, зручних і широко застосовуваних для практичних розрахунків законів розподілу випадкових величин є закон розподілу Гаусса (рис.10.1). Універсальність цього закону полягає в тому, що його вважають граничним законом, з якого випливають інші (Релея, Вейбулла, Пуассона, біноміальний тощо).

Нормальний розподіл проявляється тоді, коли зміна випадкової величини зумовлена багатьма причинами рівнозначного впливу. Йому підпорядковуються напрацювання до відмови і на відмову більшості відновлюваних і невідновлюваних виробів, які спрацьовуються і кородують, похибки вимірювань тощо.

Функцію щільності розподілу розраховують за формулою

(10.1)

Цей розподіл має два незалежних параметри: математичне сподівання m_t і середнє квадратичне відхилення S. Значення цих параметрів оцінюють за такими формулами:

; (10.2)

, (10.3)

де , – статистичні оцінки відповідно математичного сподівання і середнього квадратичного відхилення (наприклад, часу напрацювання об‘єкта до відмови або на відмову).

Математичне сподівання в цьому законі розподілу визначає положення центра кривої на осі абсцис, а середнє квадратичне відхилення – ширину фігури, описаної цією кривою (рис. 10.1). При деякому напрацювання імовірність відмови Q(t)=F(t) наближається до 1,0, а імовірність безвідмовної роботи P (t) падає до нуля (рис. 10.1).

 

Рис.10.1.Щільність ймовірності (а) та інтегральна функція

імовірності (б) нормального розподілу

 

Крива щільності розподілу випадкової величини тим гостріша і вища, чим менше значення S (рис. 10.2).

 

Рис.10.2. Щільність імовірності f(t) при нормальному розподілу

10.2.2. Логарифмічно нормальний розподіл

Розподіл випадкової величини набуває характеру логарифмічно нормального, коли за нормальним законом змінюється логарифм цієї величини. Цим законом описується напрацювання до відмови більшості деталей, особливо якщо відмови настають через втомлюваність і старіння (наприклад, підшипників кочення).

 

 

Рис. 10.3. Щільність імовірності f(t) логарифмічно нормального розподілу

 

Щільність розподілу (рис. 10.3) описується такою залежністю:

(10.4)

де μ, S - параметри, які оцінюють за результатами спостережень чи випробувань.

Так, якщо випробовують N виробів до відмови, то ;

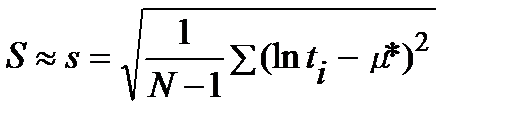, (10.5)

де μ*, s – статистична оцінка параметрів μ та s.

Імовірність безвідмовної роботи P(t) визначають залежно від значень квантилів

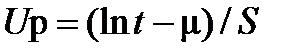. (10.6)

10.2.3. Експоненційний розподіл

Для експоненційного закону (рис. 10.4) сталою величиною є інтенсивність відмов, тобто

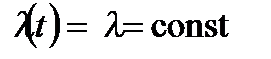; (10.7)

(10.8)

де - математичне сподівання напрацювання до відмови, що визначається на підставі оброблення результатів спостережень чи випробувань:

, (10.9)

де ─ середнє значення напрацювання; ─ поточне значення напрацювання.

Якщо напрацювання виразити в годинах, то виразиться кількістю відмов за годину.

 

Рис. 10.4. Характеристики експоненційного розподілу

 

10.2.4. Розподіл Вейбулла

Цей розподіл характеризується такими функціями (рис. 10.5):

- ймовірністю безвідмовної роботи

; (10.10)

- інтенсивністю відмов

; (10.11)

густиною розподілу

. (10.12)

Розподіл Вейбулла також має два параметри: параметр форми m > 0 і масштабний параметр t0 > 0.

Математичне сподівання і середнє квадратичне відхилення визначають відповідно так:

; (10.13)

де і - коефіцієнти (див. табл. 4.2).

Якщо протягом певного часу відмови не відбуваються, то імовірність безвідмовної роботи визначають за формулою

.

Іноді характеристики розподілу Вейбулла записують з використанням інших позначень. Наприклад, імовірність безвідмовної роботи можна подати так:

де і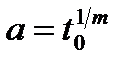

Рис. 10.5. Щільність розподілу () при розподілі Вейбулла.

 

Розподіл Вейбулла задовільно описує напрацювання до відмови підшипників та інших деталей машин, які руйнуються від утоми. Його застосовують також для оцінювання надійності вузлів підіймально-транспортних машин і механізмів.

Порядок виконання

1. Відповідно до варіанту з додатку 10, табл.. Д.10.1 (за номером в списку академічної групи) побудувати варіаційний ряд випадкових величин напрацювань, розбити його на 10 інтервалів, встановити границі інтервалів, розрахувати показники надійності, побудувати гістограму емпіричного розподілення.

2. На підставі розрахованих даних побудувати гістограму.

3. Визначити час експлуатації виробу до першого технічного огляду.

Приклад виконання

Визначити кількісні характеристики функції P(t), F(t), f(t) колінчастого вала холодильного компресора при випробуваннях його на втому по заданому варіаційному ряду напрацювання до руйнування (табл. 10.1).

 

Таблиця 10.1

Границі інтервалів напрацювань колінчастих валів холодильних компресорів до відмови, * год

[1…5)	[5…9)	[9…13)	[13…17)	[17…21)
1,0	5,1 6,1	9,0 9,5 10,0 11,0 12, 0	13,0 16, 5	17, 0
1,5	5,2 6,3	9,1 9,5 10,1 11,1 12,1	13,5 16,6	17,5
2,0	5,3 6,5	9,1 9,6 10,2 11,2 12,2	14,0	18,0
2,5	5,4 6,7	9,2 9,6 10,3 11,3 12,3	14,5	18,5
3,0	5,5 7,0	9,2 9,7 10,4 11,4 12,4	15,0	19,0
3,5	5,6 7,1	9,3 9,8 10,5 11,5 12,5	15,5	19,5
4,0	5,7 7,2	9,3 9,9 10,6 11,6 12,6	16,0	20,0
4,5	5,8 7,5	9,4 9,9 10,7 11,7 12,7	16,5	20,5
4,8	5,9 8,0	9,4 9,9 10,8 11,8 12,8	16,5
4,9	6,0 8,9	9,4 9,9 10,9 11,9 12,9	16,5
*N=(ti+ti+1)/2 – кількість випробуваних колінчастих валів

 

– середнє напрацювання вала в інтервалі напрацювання;

– частість настання відмови;

– щільність розподілу випадкової величини;

– імовірність відмови колінчастого вала;

– імовірність безвідмовної роботи вала.

Результати розрахунку показників надійності занесені до табл. 10.2.

Емпіричне розподілення подаємо у вигляді гістограми.

При побудові гістограми над кожним відрізком абсцис, відповідних інтервалу, будується прямокутник, площа якого пропорційна частоті або частості. При однаковій ширині інтервалів частоті або частості пропорційна висота прямокутників.

 

Таблиця 10.2

Результати розрахунку показників надійності

Номер інтервалу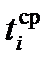
	1…5			0,100	0,10	0,90
	5…9			0,200	0,30	0,70
	9…13			0,500	0,80	0,20
	13…17			0,120	0,92	0,08
	17…21			0,080	1,00	0,00

При великій кількості інтервалів плавна крива, що описує їх границі наближається до кривої закону розподілу.

10.4. Контрольні запитання.

1) Що таке гістограма? Як і з якою метою її будують?

2) Назвіть основні характеристики законів розподілу випадкових величин.

3) Як пов’язані між собою щільність розподілу відмов і безвідмовність виробів?

4) Які області застосування функцій частоти відмов 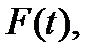інтенсивності відмов і параметра потоку відмов 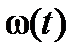у теорії надійності?

5) У яких випадках моделі відмов описуються ймовірнісними законами надійності (нормальним, логарифмічно нормальним, гамма, Пуассона, Вейбулла, експоненційним)?