Задание.
1. Используя группированную выборку из задачи№1, проверьте на уровне  гипотезу
гипотезу  : выборка взята из генеральной совокупности, распределенной по закону
: выборка взята из генеральной совокупности, распределенной по закону 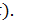
2. Неизвестные параметры распределения  , если это необходимо, найдите методом моментов или методом максимального правдоподобия по выборке.
, если это необходимо, найдите методом моментов или методом максимального правдоподобия по выборке.
3. Постройте совмещенные графики гистограммы относительных частот и плотности, соответствующей функции распределения 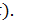
| Номер варианта
| Закон распределения 
| Уровень доверия
| Номер варианта
| Закон распределения 
| Уровень доверия
|
|
| 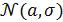
| 0,02
|
| Равномерный на 
| 0,01
|
|
| 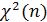
| 0,05
|
| Фишер 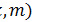
| 0,05
|
|
| Показательный
| 0,05
|
| 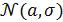
| 0,02
|
|
| Равномерный на 
| 0,02
|
| 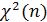
| 0,05
|
|
| Фишер 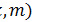
| 0,1
|
| Показательный
| 0,01
|
|
| 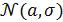
| 0,02
|
| Равномерный на 
| 0,02
|
|
| 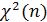
| 0,05
|
| Фишер 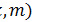
| 0,1
|
|
| Показательный
| 0,05
|
| Гамма- распределение 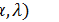
| 0,05
|
|
| Равномерный на 
| 0,01
|
| Логистическое 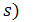
| 0,1
|
|
| Фишер 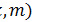
| 0,05
|
| Логнормальное 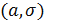
| 0.05
|
|
| 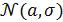
| 0,01
|
| Логнормальное 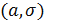
| 0,05
|
|
| 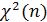
| 0,05
|
| 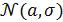
| 0,1
|
|
| Показательный
| 0,02
|
| Гамма- распределение 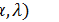
| 0,02
|
Таблица плотностей некоторых распределений
|
| Закон распределения
| Плотность
|
|
| Нормальный 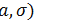
| 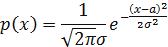
|
|
| Хи - квадрат 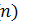
| 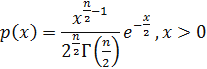
|
|
| Показательный 
| 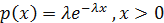
|
|
| Равномерный 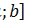
| 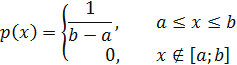
|
|
| Фишер 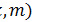
| 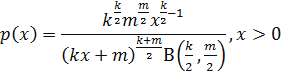
|
|
| Гамма-распределение 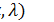
| 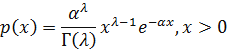
|
|
| Логистическое 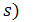
| 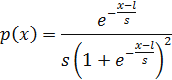
|
|
| Логнормальное 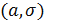
| 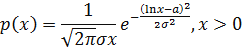
|
Пример выполнения задания
Гипотеза  : выборка взята из генеральной совокупности, распределенной по показательному закону,
: выборка взята из генеральной совокупности, распределенной по показательному закону,
Альтернатива  : Выборка не подчиняется показательному закону
: Выборка не подчиняется показательному закону
Уровень 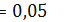
Выборка:
Группировка (уже выполненав задаче 1)
Оценка параметра:
Вычисление статистики  и квантили
и квантили 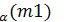 :
:
Проверка.  
|


Вычисление  (объединение последних двух интервалов)
(объединение последних двух интервалов)

Вычисление квантили: 
Комментарий: число степеней свободы 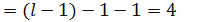
 гипотезу
гипотезу  : выборка взята из генеральной совокупности, распределенной по закону
: выборка взята из генеральной совокупности, распределенной по закону 
 , если это необходимо, найдите методом моментов или методом максимального правдоподобия по выборке.
, если это необходимо, найдите методом моментов или методом максимального правдоподобия по выборке.


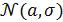

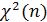
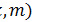
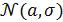

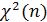
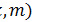
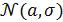

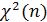
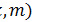
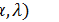

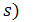
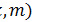
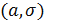
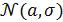
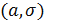
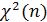
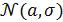
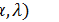
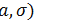
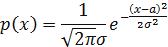
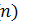
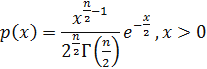

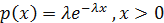
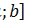
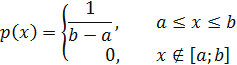
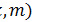
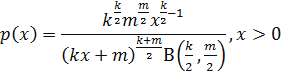
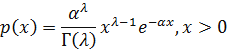
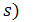
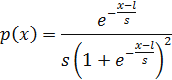
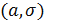
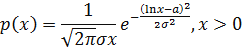
 : выборка взята из генеральной совокупности, распределенной по показательному закону,
: выборка взята из генеральной совокупности, распределенной по показательному закону, : Выборка не подчиняется показательному закону
: Выборка не подчиняется показательному закону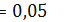























 и квантили
и квантили 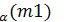 :
:








 (объединение последних двух интервалов)
(объединение последних двух интервалов)


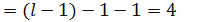
 2017-12-14
2017-12-14 299
299






