ЗАНЯТИЕ № 4
Сравнение бесконечно малых и бесконечно больших функций.
Эквивалентности.
Необходимые сведения.
1. Пусть  и
и 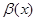 – две бесконечно малые функции при
– две бесконечно малые функции при  . Рассмотрим
. Рассмотрим 
 .
.
Если 
 =0, то бесконечно малая
=0, то бесконечно малая  – более высокого порядка, чем
– более высокого порядка, чем 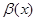 .
.
Если 
 =
=  , то бесконечно малая
, то бесконечно малая  – более низкого порядка чем
– более низкого порядка чем 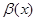 , или,
, или,
наоборот: 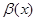 – более высокого порядка, чем
– более высокого порядка, чем  .
.
Если 
 =
= 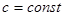 , то бесконечно малые
, то бесконечно малые  и
и 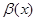 – одного порядка малости.
– одного порядка малости.
Если же эта константа  , то две бесконечно малые называются эквивалентными при
, то две бесконечно малые называются эквивалентными при 
и это обозначается 
 ,
, 
2. Пусть  и
и  – две бесконечно большие функции при
– две бесконечно большие функции при  . Рассмотрим
. Рассмотрим 
 .
.
Если 
 =
=  , то
, то  – бесконечно большая более высокого порядка (степени роста), чем
– бесконечно большая более высокого порядка (степени роста), чем  . Другими словами,
. Другими словами,  растёт быстрее, чем
растёт быстрее, чем  при
при  .
.
Если 
 =0, то
=0, то  – бесконечно большая более низкого порядка, чем (растёт медленнее, чем
– бесконечно большая более низкого порядка, чем (растёт медленнее, чем  , при
, при  ).
).
Если 
 =
= 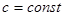 , то бесконечно большие
, то бесконечно большие  и
и  – одного порядка роста
– одного порядка роста
при  .
.
Если же эта константа  , то две бесконечно большие
, то две бесконечно большие  и называются
и называются
эквивалентными при  и это обозначается:
и это обозначается: 
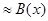 ,
,  .
.
3. Таблица основных эквивалентностей бесконечно малых величин:
Эквивалентности, следующие
из первого замечательного предела:  
| Эквивалентности, следующие
из второго замечательного предела:  
|
 при при 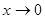
| 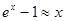 при при 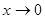
|
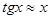 при при 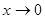
|  при при 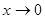
|
 при при 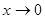
| 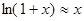 при при 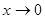
|
 при при 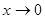
|  при при 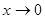
|
 при при 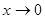
|  при при 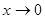
|
4. Если 
 ,
,  ,
, 
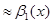 ,
,  , то
, то 
 =
= 

Математический анализ 1 курс 1 семестр
Задачи для решения в аудитории.
1.Определить порядок малости  относительно
относительно 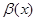
 при
при  :
:
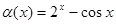
2.Доказать, что  имеет 2-й порядок малости относительно
имеет 2-й порядок малости относительно  при
при  :
:
 ,
, 
3.Вычислить пределы, используя эквивалентные бесконечно малые:
3.1)  3.2)
3.2)  3.3)
3.3) 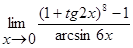 3.4)
3.4) 
3.5)  3.6)
3.6)  3.7)
3.7) 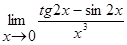 3.8)
3.8) 
3.9)  3.10)
3.10)  3.11)
3.11)  3.12)
3.12) 
4.Определить порядок роста бесконечно большой  относительно
относительно  =
=  при
при  :
:

5.Подобрать такие константы С и k, чтобы 
 ,
,  :
:
5.1)  ,
, 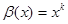 ,
, 
5.2)  ,
, 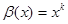 ,
, 
Домашнее задание.
- Таблицу эквивалентностей выучить наизусть, уметь выводить
2. Ефимов – Поспелов, том 2, №№ 5.347-5.357, 5.359, 5.364-5.376
3*. Кудрявцев, Кутасов, Чехлов, Шабунин, том1, гл.2, параграф 9, стр.189-192,№№ 44 - 52, 58
При подготовке к самостоятельной работе № 4 обратите внимание на вычисление пределов вида:
а)  в)
в)  с)
с) 
 2017-10-31
2017-10-31 553
553






