Основные положения алгебры логики

Математической основой описания работы логических устройств является алгебра логики. Логическая переменная принимает значения только из бинарного множества {0; 1}, и для любой логической функции областью определения и областью значений является также бинарное множество.

Основные функции (операции) в алгебре логики:

─ отрицание: ;

─ конъюнкция: или или или ;

─ дизъюнкция: или ;

─ сложение по модулю 2: .

Наиболее наглядным представлением логической функции, описывающей работу схемы, является таблица истинности – таблица, в которой указано значение выходного сигнала для всех комбинаций входных переменных. В табл. 4.1 представлены таблицы истинности для основных логических функций двух переменных.

Таблица 4.1

x 1	x 2

При анализе и проектировании логических устройств широко используются основные тождества алгебры логики:

Операции с 0 и 1:

Свойство коммутативности:

Свойство ассоциативности:

Свойство дистрибутивности:

Правила повторения: x x = x; .

Правила отрицания:

Правила поглощения:

Правила склеивания:

Правила де Моргана:

Универсальный способ доказательства любого тождества – сравнение таблиц истинности.

Ряд тождеств допускает обобщение на произвольное число переменных. Например, правила де Моргана:

Соотношения в алгебре логики записывают обычно с помощью функций конъюнкции, дизъюнкции и отрицания. Через эти функции выражаются при необходимости и другие функции алгебры логики. Так, например, часто использующаяся при обработке дискретных сигналов операция сложения по модулю 2 может быть представлена (и реализована в логической схеме) в виде: Впрочем, для этой операции также можно записать ряд тождеств. Так, например, операция коммутативна, ассоциативна и дистрибутивна относительно конъюнкции:

Справедливы также следующие тождества:

Логические элементы

Логическими элементами (ЛЭ) называют функциональные устройства, с помощью которых реализуются элементарные логические функции. Современные ЛЭ выполняются в виде ИМС различной степени сложности. ЛЭ дают возможность воспроизводить логические переменные с помощью электрических сигналов. В судовых системах управления практически повсеместно используются ЛЭ, выполненные в соответствии с положительной логикой: высокий уровень напряжения соответствует единице, низкий – нулю.

Логический элемент И реализует операцию конъюнкции, логический элемент ИЛИ – дизъюнкции, логический элемент НЕ – отрицания, логический элемент ИСКЛЮЧАЮЩЕЕ ИЛИ – операцию сложения по модулю 2. Зачастую названия перечисленных ЛЭ используются и для обозначения логических операций.

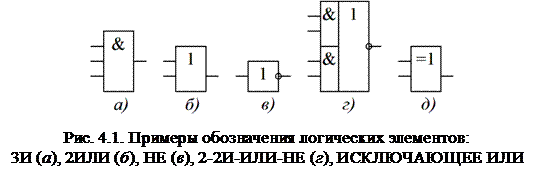На рис. 4.1 изображены в соответствии со стандартами ЕСКД примеры условных графических обозначений основных ЛЭ, а также составных ЛЭ, реализующих более сложные логические функции.

Основные параметры логических элементов:

1. Ток потребления I _пот – ток, потребляемый микросхемой (которая может содержать несколько ЛЭ) от источника питания. Иногда указываются отдельно токи потребления в состоянии 1 и в состоянии 0 .

2. Напряжения высокого U ¹ и низкого U ⁰ уровней,определяющиеся технологией изготовления микросхемы и установленной величиной питающего напряжения.

3. Входные ток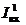и и при входных напряжениях соответственно высокого и низкого уровня.

4. Выходные токи и .

5. Коэффициент разветвления по выходу К _раз , показывающий, какое число входов ЛЭ этой же серии может быть подключено к выходу данного ЛЭ.

6. Время задержки распространения сигнала при включении и при выключении – интервал времени между входным и выходным импульсами при переходе напряжения на выходе микросхемы соответственно из 1 в 0 и из 0 в 1, измеренный на уровне половины амплитуды сигнала (рис. 4.2). Иногда указывается среднее время задержки распространения