Лабораторная работа №6
ИНТЕГРАЛ
Цель: закрепить знания по теме «Интеграл», научиться:вычислять интегралы путем применения таблицы и свойств интегралов, и с помощью простейших преобразований, приводящих подынтегральное выражение в табличному интегралу; выработать навык интегрирования подстановкой, установить связь подстановки с внесением под знак дифференциала;установить, для каких интегралов применяется интегрирование по частям, какая часть под интегрального выражения обозначается за 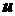 и какая за
и какая за 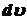 ; вычислять определенный интеграл методами подстановки и по частям.
; вычислять определенный интеграл методами подстановки и по частям.
Ход выполнения работы:
I. Ответить на контрольные вопросы:
1. В чем состоит задача интегрального исчисления?
2. Определение первообразной функции.
3. Определение неопределенного интеграла.
4. Сформулируйте свойства неопределенного интеграла.
II. Выполнить практическое задание.
Методические рекомендации:
1. В следующих равенствах заполнить пропущенные места:
1) 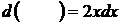
Решение:
Дифференциал функции равен произведению производной функции на дифференциал независимой переменной, значит нужно найти функцию, производная которой равна 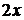 . Это
. Это 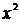 .
.
2) 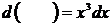 Ответ:
Ответ: 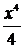
3) 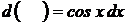 Ответ:
Ответ: 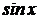
4) 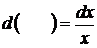 Ответ:
Ответ: 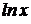
5) 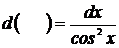 Ответ:
Ответ: 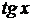
6) 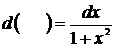 Ответ:
Ответ: 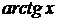
2. Найти интегралы:
Методические рекомендации:
Обратить внимание та то, что таблицу интегралов надо знать наизусть, чтобы свободно ею пользоваться.
ТАБЛИЦА ИНТЕГРАЛОВ
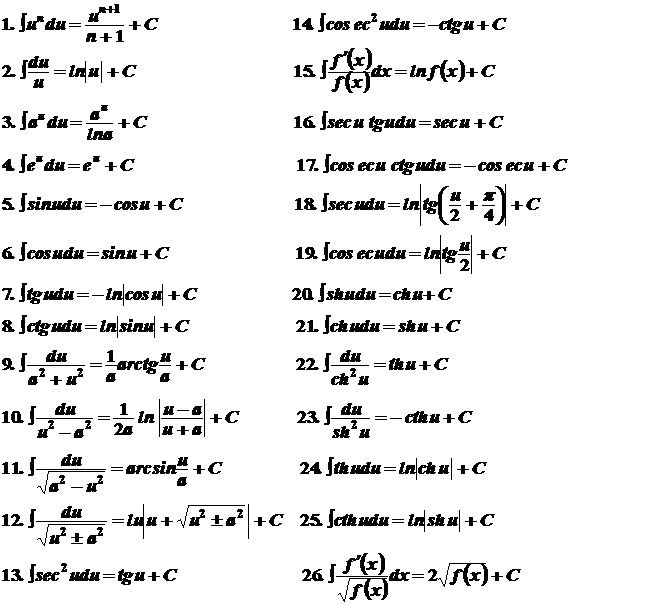
Найти интегралы:
1) 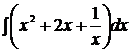
Решение:
Студент должен сформулировать правила интегрирования (интеграл от суммы и постоянном многочлене) и взять интегралы по формулам:
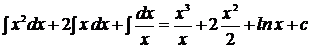
2) 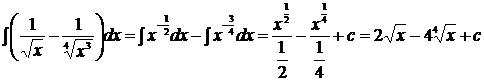
3) 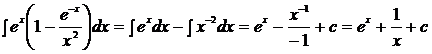
4)
4) 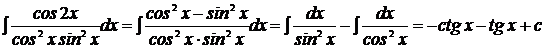
разделим числитель почленно на знаменатель
5)Вычислить интеграл 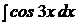
Решение:
Интеграл не является табличным. Табличный выглядит так: 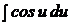 , для того, чтобы данный интеграл стал табличным, надо иметь
, для того, чтобы данный интеграл стал табличным, надо иметь 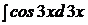 , но
, но 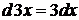 , т.е. внесение постоянного множителя
, т.е. внесение постоянного множителя 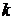 под знак дифференциала увеличивает дифференциал в
под знак дифференциала увеличивает дифференциал в 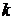 раз:
раз: 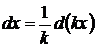 поэтому имеем:
поэтому имеем: 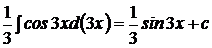
7) 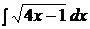
Под знаком интеграла степенная функция с показателем 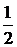 , но не табличный, т.к. в основании степени и под знаком дифференциала стоят разные выражения.
, но не табличный, т.к. в основании степени и под знаком дифференциала стоят разные выражения.
Рассмотрим 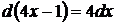 т.е.
т.е. 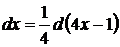
Получим: под знаком дифференциала, стоящего в интеграле, можно ввести любое постоянное слагаемое.
Вернемся к вычислению интеграла:
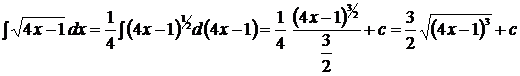
3. Найти инреграл, применив интегрирование подстановкой:
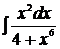
Методические рекомендации:
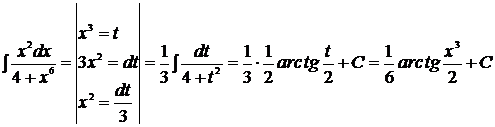
или 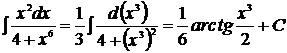 .
.
Найти инрегралы, применив метод интегрирования по частям.
Методические рекомендации:
1. Вычислить: 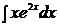
Решение:
Видим, что из двух множителей 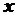 и
и 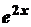 , первый упрощается после дифференцирования, а второй не изменяется, ни от дифференцирования, ни от интегрирования, получим:
, первый упрощается после дифференцирования, а второй не изменяется, ни от дифференцирования, ни от интегрирования, получим:
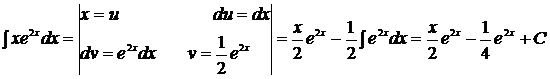
2. Вычислить: 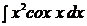
Решение:
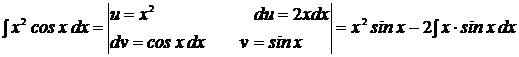
видим, что множитель 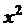 изменил степень, она стала на единицу меньше
изменил степень, она стала на единицу меньше 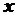 , еще раз применим интегрирование по частям
, еще раз применим интегрирование по частям
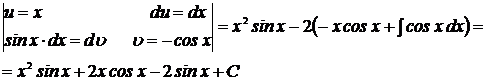 :
:
Замечание: в рассмотренных примерах мы следовали общему указанию: выбирать за 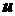 множитель, упрощающийся от дифференцирования.
множитель, упрощающийся от дифференцирования.
Попробуем отступить от этого указания.
Пусть 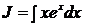 .
.
При решении этого примера мы принимаем за 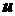 множитель
множитель 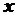 . Попробуем теперь принять за
. Попробуем теперь принять за 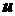 множитель
множитель 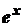 , хотя он не упрощается от дифференцирования. Тогда
, хотя он не упрощается от дифференцирования. Тогда
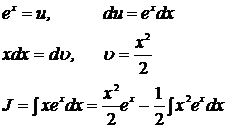
Хотя это равенство верное, но оно бесполезно, т.к. правый интеграл сложнее левого.
3. Вычислить: 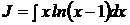
Решение:
В этом примере от дифференцирования упрощается трансцендентный множитель, его и примем за 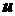 .
.
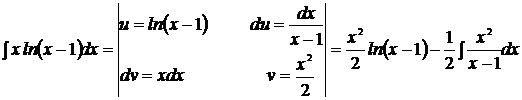
Последний интеграл от неправильной рациональной дроби и надо исключить целую часть:
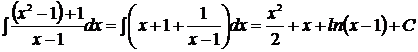
Значит: 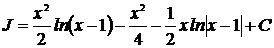 .
.
4. Вычислить определенный интеграл:
Методические рекомендации:
1. 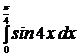 .
.
Решение:
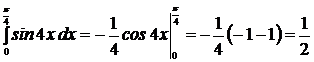 .
.
2. 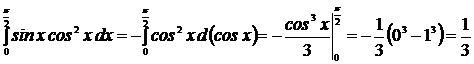 .
.
3. 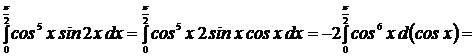
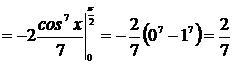 .
.
4. Найти площадь фигуры, ограниченной параболами 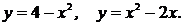
Методические рекомендации:
Решение. Найдём точки пересечения парабол. Для этого решим систему уравнений 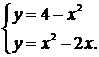
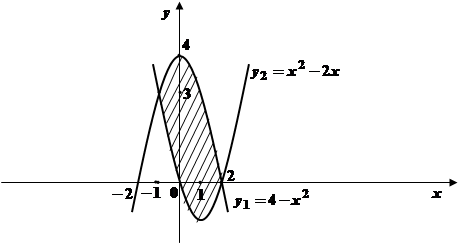 |
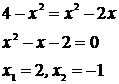
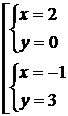 .
.
Получили две точки 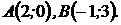
Найдём площадь фигуры:
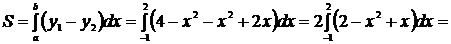
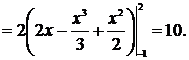
Варианты заданий:
1 и 6 вариант
1. 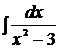 2.
2. 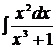 3.
3. 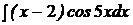
4. Найти площадь криволинейной трапеции, ограниченной линиями 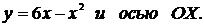
2 и 7 вариант
1. 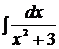 2.
2. 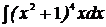 3.
3. 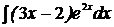
4. Найти площадь криволинейной трапеции, ограниченной линиями 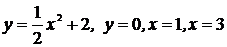
3 и 8 вариант
1. 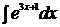 2.
2. 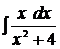 3.
3. 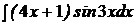
4. Найти площадь криволинейной трапеции, ограниченной линиями 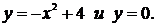
4 и 9 вариант
1. 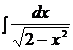 2.
2. 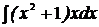 3.
3. 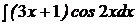
4. Найти площадь криволинейной трапеции, ограниченной линиями 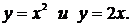
5 и 10 вариант
1. 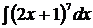 2.
2. 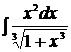 3.
3. 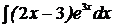
4. Найти площадь криволинейной трапеции, ограниченной линиями 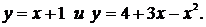
Вариант для бонусных баллов
1. 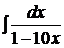 2.
2. 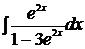 3.
3. 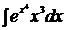 3.
3. 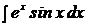
4.Найти площадь фигуры, ограниченную линиями 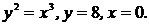
 2017-12-14
2017-12-14 764
764






