Аксиомы и теорема Эрроу. Голосование. Правила: простого большинства, Гудмана-Марковица, Кондорсе, Дельфи. Метод Саати. Обработка экспертной информации в виде нескольких ранжировок (корреляция Спирмена, Кендалла, коэффициент конкордации).
Под принятием группового решения обычно понимают выработку общего для всех участников группы соглашения по рассматриваемому процессу или объекту на основе субъективных интересов, предпочтений и целей, высказанных участниками переговоров.
В тех случаях, когда объективной информации оказывается недостаточно для определения численных значений требуемого критерия при принятии решения, должны использоваться субъективные оценки, основанные на накопленном опыте, знаниях, идеях, мнениях и догадках специалистов, привлеченных к выработке субъективной оценки. Получение объективных оценок базируется на следующих общих положениях:
1) аксиома несмещенности (единогласия), которая утверждает, что мнение большинства компетентно;
2) аксиома транзитивности, утверждающая, что субъективные оценки транзитивны;
3) аксиома полноты (совершенности) – для любых двух альтернатив группа должна указать лучшую;
4) аксиома независимости - при сравнении двух альтернатив группа забывает о других альтернативах.
Теорема Эрроу: если групповое правило ПР удовлетворяет аксиомам 1-4, то это – диктатура. Или: не существует демократической процедуры ПР, а если диктатура отвергается, то выработка группового решения не происходит автоматически ® основное условие успешности согласования групповых решений, проводимого не с позиции силы, – удовлетворение интересов договаривающихся сторон на основе компромисса, то есть достижение условий, при которых в определенном выигрыше оказывается каждая договаривающаяся сторона (рисунок - Этапы принятия решений).
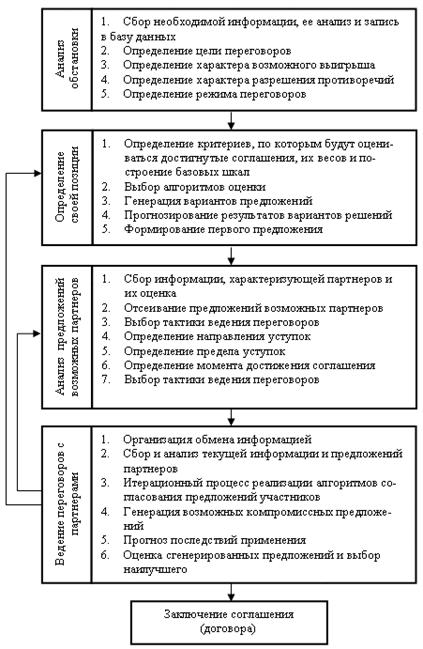
Рисунок - Этапы принятия решений
Экспертиза
В процессе неформального синтеза после выдвижения множества идей необходимо окончательно принять к реализации какую-то одну из них, поскольку исследовать до конца детально все идеи довольно сложно. Чтобы отобрать лучшую (лучшие) из них, проводят их экспертизу.
Для этого коллектив экспертов анализирует идеи, и каждый эксперт выставляет каждой идее свою собственную оценку. Условиями проведения экспертизы является коллектив экспертов и перечень оцениваемых идей. Результатом первого этапа экспертизы является матрица оценок. Далее с помощью определенного выбранного метода учитывают совместно все эти оценки и выбирают лучшую идею.
К экспертизе прибегают, когда необходимо сделать выбор из множества возможных идей, решений, проектов. Экспертиза — целесообразный отбор одного решения из множества возможных, полученных на предыдущем этапе «Генерация идей» (см. Неформальный синтез).
Существует много методов проведения экспертизы: голосование, ранжирование, попарное сравнение, разбиение на классы. Рассмотрим некоторые из них.
Голосование
Голосование можно применять только в том случае, если мнений, которые предложены к рассмотрению, меньше, чем собравшихся.
Примером, иллюстрирующим этот тезис, является решение профкома о выделении квартиры. Представитель каждого отдела предприятия, участвующий в заседании профкома, если он честен, должен голосовать только за своего представителя. Таким образом, никто и никогда не наберет большинство голосов. Задача попросту не решается. Или решается нечестными способами, например, сговором двух представителей, попеременно голосующих то за отдел А, то за отдел Б, и побеждающих всегда двумя голосами против остальных.
Простейший способ голосования — выбор большинством голосов. Он имеет свои достоинства (простота) и недостатки (решение принимается неквалифицированным большинством).
Данный способ можно существенно улучшить.
- Голосование большинством 2/3. Для принятия решения требуется набрать 2/3 голосов. Такое правило применяется в особо ответственных случаях, повышая порог принятия решения. Но при этом метод часто приводит в тупик, так как необходимого количества голосов набрать какому-то одному из проектов достаточно трудно.
- Голосование с правом вето. В этом случае любой эксперт имеет право заблокировать общее намечающееся решение одним своим голосом, если решение ему не выгодно или опасно. Это еще более жесткая процедура голосования. Способ применяется в сверхответственных ситуациях (например, принятие решений в ООН).
- Талонное голосование. Голосовать можно только при наличии талона. Талонов меньше, чем голосований в течение оговоренного отрезка времени. Например, на 12 совещаний в год каждому эксперту выдается 8 талонов. Таким образом, если эксперт чувствует себя не вполне компетентным по какому-то вопросу, он не вмешивается в процесс голосования, сохраняя талон для более важного для него вопроса. Метод существенно улучшает процедуру голосования, заставляя ответственно оценивать не только проекты, но и себя.
- Туровое голосование. В первом туре голосования отбирается как результат 2-3 проекта, которые набирают большинство голосов или проходят установленный порог. Во втором туре все эксперты голосуют снова, но только уже за эти 2-3 отобранных проекта. В качестве примера можно привести выборы президента в России или во Франции. Недостатком такого голосования является то, что эксперт во втором туре вынужден голосовать не за то решение, которое ему нравится, а за одно из тех, которые прошли во второй тур. Возникает иллюзия выбора.
- Туровое голосование можно существенно улучшить, если дать возможность экспертам знакомиться с результатами голосования после каждого тура и не убирать проекты из матрицы от тура к туру. В результате такой процедуры эксперты, видя и оценивая общий результат, могут менять собственные предпочтения, исключая случайность и приходя к равновесному мнению. Этот метод получил название «метод Дельфы».
Пример турового голосования. Пусть имеется семеро кандидатов на получение премии: Дмитриев (Д), Иванов (И), Кузнецов (К), Лукьянов (Л), Михайлов (М), Петров (П), Сидоров (С). Премию могут получить лишь трое лучших. В первом туре каждый эксперт (в примере их пятеро) оценивает каждого из кандидатов и ставит его на то или иное место (см. табл. 36.1).
| Таблица 36.1. Распределение мест проектов, данное коллективом экспертов (первый тур) | ||||||||||||||||||||||||||||||||||||||||||||||||
|
Далее подсчитываются очки. Трое экспертов присвоили Иванову первое место, один эксперт дал ему второе место и еще один — третье. Зная это, подсчитываем общее число очков для Иванова: 3 · 1 + 1 · 2 + 1 · 3 = 8. Таким же образом подсчитываются очки для всех остальных кандидатов. Результаты сводятся в таблицу (см. табл. 36.2).
| Таблица 36.2. Итоги первого тура | ||||||||||||||||||||||||
|
Чем меньше очков у кандидата, тем более высокое у него место. Это непосредственно следует из принципа подсчета очков. Как видим, после первого тура призовые места достаются Иванову, Лукьянову и Сидорову.
После опубликования результатов выявляется и недостаток голосования, так как часть экспертов не удовлетворена результатами. Например, кандидат Лукьянов (см. табл. 36.1), которому никто из экспертов не давал ни одного из призовых мест, ибо никто не видел Лукьянова как достойного кандидата на премию, получил второе место, а вместе с ним и премию. Второй эксперт недоволен тем, что Сидоров вошел в тройку призеров. И если бы он голосовал снова, то он бы поменял Сидорова и Петрова местами, заставив опуститься Сидорова в общем рейтинге. Так как есть эксперты, заинтересованные в изменении результатов (путем перестановки проектов), то имеет смысл провести второй тур.
Посмотрим, что будет делать первый эксперт во втором туре: скорее всего, он поменяет местами Петрова и Иванова, переставит Сидорова на второе место, так как ему «наступают на пятки» конкуренты Дмитриев и Кузнецов, а Иванова, которому ничего не угрожает, поставит на третье место.
Так же, но по-своему, поступят другие эксперты. Поэтому результаты голосования от тура к туру будут меняться.
Например, после второго тура матрица оценок может выглядеть так (см. табл. 36.3).
| Таблица 36.3. Распределение мест проектов, данное коллективом экспертов (второй тур) | ||||||||||||||||||||||||||||||||||||||||||||||||
|
Кроме таблицы результатов удобно вычислять таблицу неудовлетворенности экспертов. Например, подсчитывая сумму разностей по каждому эксперту между желательным распределением проектов по местам и общим результатом тура. Если эксперт действует логично, показатель неудовлетворенности от тура к туру, в принципе, должен уменьшаться. Хотя нулевым он станет вряд ли, так как неудовлетворенность одного эксперта уменьшается за счет увеличения неудовлетворенности другого. Поэтому процедура должна прийти к равновесному состоянию за счет действия всех экспертов одновременно, понижающих собственные показатели неудовлетворенности.
Туровая процедура продолжается до тех пор, пока ни один эксперт в одиночку не в силах будет изменить получившийся порядок (результат). То есть, притом, что какие-то эксперты могут остаться неудовлетворенными, изменить результат голосования они не смогут. Технически это означает, что результат в нескольких последовательных турах перестанет меняться. Его и принимают в качестве ответа.
Рассмотрим второй класс методов экспертизы.
Ранжирование
Ранжирование есть упорядочение, разбиение множества на элементы с введением между ними некоторого порядка, в данном случае порядка «лучше-хуже».
Пусть четверо экспертов расставляют проекты A, B, C и D по рангам (местам), см. табл. 36.4.
| Таблица 36.4. Распределение мест проектов, данное коллективом экспертов | |||||||||||||||||||||||||
|
Ранжирование>Метод «Медиана Кемени»
Вычисляются значения rij — расстояние между мнениями i -го и j -го экспертов. Вычислять расстояние между двумя векторами (вектор — это мнение эксперта по кортежу проектов) можно по-разному. Расстояние в математике называется нормой. Есть пифагорова норма, манхэттенская, Минковского и т. д. (подробнее см. в курсе «Искусственный интеллект» или «Высшая математика»). Например, вычислим в матрице (см. табл. 36.4) расстояние между мнениями эксперта 1 и эксперта 2 по манхэттенской норме:
r 12 = |1 – 1| + |2 – 3| + |3 – 2| + |4 – 4| = 0 + 1 + 1 + 0 = 2.
Итак, расстояние мнений по манхэттенской норме — это сумма разностей (по абсолютной величине) мнений двух экспертов по каждому проекту.
Эти значения заносятся в таблицу (матрицу расстояний). Затем вычисляются значения Ri — расстояние от i -го эксперта до всех остальных — как сумма расстояний между мнением этого эксперта и остальных экспертов (см. табл. 36.5).
| Таблица 36.5. Расчет расстояний между мнениями экспертов | ||||||||||||||||||||||||||||||||
|
Среди вычисленных суммарных расстояний ищется минимум из Ri. Мнение соответствующего i -го эксперта (с минимальным R) является самым средним и объявляется результатом экспертизы. Геометрическая интерпретация показывает, что мнение данного эксперта находится примерно в центре многогранника, образованного вершинами, каждая из которых представляет собой мнение отдельного эксперта, а ребра — расстояния между мнениями экспертов. Как известно, центр — место, наиболее приближенное ко всем вершинам (мнениям) фигуры одновременно.
Система координат для построения многогранника образована проектами. Таким образом, 4 проекта образуют 4-хмерное пространство. По осям координат откладывают баллы, полученные проектом у данного эксперта. Тогда мнение эксперта — точка в пространстве проектов.
На рис. 36.1 показано четырехмерное пространство, образованное проектами АВСD. Чтобы найти точку — мнение эксперта — в четырехмерном пространстве, надо отложить вдоль оси A число баллов, поставленное экспертом проекту A. Далее провести через полученную точку линию, параллельную следующей оси B и отложить на этой линии число баллов, поставленное экспертом проекту B. Через полученную точку снова провести линию, параллельную оси C, отложив на ней число баллов, поставленное экспертом проекту C. И, наконец, через полученную точку провести линию, параллельную D, отложив на ней число баллов, поставленное экспертом проекту D. Точка, соответствующая мнению эксперта в четырехмерном пространстве, найдена. Так же следует найти точки — мнения экспертов 2, 3, 4. Соединив точки линиями, получим многогранник мнений экспертов.
| |
| Рис. 36.1. Многогранник мнений экспертов 1, 2, 3, 4 в четырехмерном пространстве проектов АВСD |
Очевидно, что вы можете построить любое количество осей и отразить на плоскости пространство любой размерности (см. лекцию 16. Понятие размерности пространства в дисциплине «Компьютерная графика»). То, что вы видите на рис. 36.1, есть проекция фигуры из четырехмерного пространства на двухмерной плоскости экрана. В зависимости от того, насколько удачно вы расположите оси (точнее сказать, проекции осей) на плоскости, рисунок будет более или менее наглядным. Поворачивая оси, можно добиться наглядного изображения. Это называется найти удачный ракурс рассмотрения многомерной фигуры. Рассматривая рис. 36.1, обратите внимание на то, что точка 1 (символизирует мнение эксперта 1 по поводу проектов A, B, C, D) находится ближе всех к мнениям остальных экспертов, в отличие от точек 2, 3, 4. Рассматривая многогранник с разных сторон (поворачивая оси) можно убедиться, что так точка выглядит с любого ракурса. Значит, мнение эксперта 1 — среднее и является решением.
Можно, разумеется, изображать эту фигуру и в трехмерном пространстве, и двухмерном, и даже одномерном или нульмерном (см. рис. 36.2), что является для вас более привычным. Такие рисунки являются сечениями четырехмерного пространства по одной или двум осям. Это вопрос удобства мышления. Обычно рисуют сразу несколько сечений, желательно во взаимоперпендикулярных плоскостях, чтобы попытаться восстановить общий вид фигуры по нескольким частным видам В УМЕ, разглядывая их ОДНОВРЕМЕННО. Так поступают, например, при работе с чертежами.
На рис. 36.2 показано сечение четырехмерного пространства для трех осей (A, B, C) и различных пар двух осей. (Проекции на одномерные оси и на нульмерную ось постройте сами). Но и из этих рисунков видно, что мнение эксперта 1 является средним, так как всегда лежит внутри многогранника (1-2-3-4).
| |
| Рис. 36.2. Проекции многогранника мнений экспертов на оси проектов АВСD |
Отметим, что самая удаленная от центра вершина характеризует самое ненадежное мнение и может этим характеризовать самого эксперта.
В нашем примере матрица расстояний будет выглядеть так (см. табл. 36.6).
| Таблица 36.6. Расчет значений расстояний между мнениями экспертов | ||||||||||||||||||||||||||||||
|
Очевидно, что наименьшее расстояние от остальных мнений — у эксперта 1, поэтому его мнение объявляется результатом.
Ответ: проект A — 1 место, проект B — 2, проект C — 3, проект D — 4. Наилучшим проектом является проект A.
Ранжирование>Метод большинства
На первое место ставится тот проект, которому большинство экспертов присвоило первое место. На второе место ставится тот проект, которому большинство экспертов присвоило второе место и так далее.
В нашем примере (см. табл. 36.4) проект A займет в итоге первое место, так как трое экспертов отдали ему первое место. Проекты B и C поделят второе и третье места, так как двое экспертов отдали им третье место. Проект D займет четвертое место, так как три эксперта отдали ему четвертое место.
Ответ: проект A — 1 место, проект B и C делят 2 и 3 место, проект D — 4 место. Наилучшим проектом является проект A.
Примечание: можно немного уточнить решение задачи, разрешив спор за 2 и 3 место в пользу проекта B. Если посмотреть внимательно, сравнивая окончательно между собой проекты B и C, то проект B более предпочтителен, чем C, поскольку занимает дополнительно места 2 и 1, а проект C — только места 2 и 4.
Важное замечание. Ответы задачи, полученные методом «Медиана Кемени» и методом большинства, совпали, хотя это происходит не всегда. Решения, полученные разными методами, могут слегка отличаться друг от друга. Но в целом решение устойчиво. В ряде случаев отдельные методы могут не сработать, поэтому экспертизу проводят несколькими методами, а затем выводят общий ответ.
Ранжирование>Альтернатива Кондорсе
Снова рассмотрим наш пример (табл. 36.7).
| Таблица 36.7. Распределение мест проектов, данное коллективом экспертов | |||||||||||||||||||||||||
|
Сначала для каждой пары проектов (i и j) подсчитаем, какое количество Sij экспертов считает, что i -ый проект лучше, чем j -ый, и какое количество Sji экспертов считает наоборот (см. табл. 36.8).
| Таблица 36.8. Расчет отношений «лучше-хуже» между проектами | ||||||||||||||||||||||||||||
|
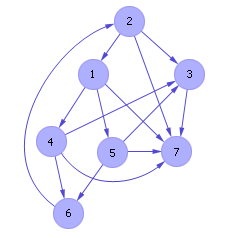
Далее на графе стрелками покажем отношения между парами проектов (см. рис. 36.3). Стрелка от i -го проекта в графе к j -му указывает, что i -му проекту отдали предпочтение больше экспертов, чем j -му. Например, стрелка от A направлена к B, так как проект A лучше проекта B (трое экспертов предпочли проекту B проект A, и лишь только один эксперт — наоборот).
| |
| Рис. 36.3. Граф предпочтений проектов АВСD |
Теперь упорядочим граф, приведя его к ярусно-параллельной форме (ЯПФ) (см. рис. 36.4).
| |
| Рис. 36.4. Граф предпочтений ABCD в ярусно-параллельной форме |
Приведение графа к ЯПФ есть приведение его к такой форме, где в верхних ярусах находятся вершины, в которые нет входящих стрелок из вершин, лежащих в нижних ярусах. Алгоритм построения ЯПФ графа разбирается в дисциплине «Дискретная математика». Итак, ЯПФ показывает, что вершиной, в которую нет стрелок, является вершина A, следовательно, абсолютным лидером среди проектов является проект A. Проект A лучше B, одновременно он лучше C, одновременно он лучше D. Далее, среди оставшихся проектов (BCD) проект B лучший, так как он одновременно лучше C и D. И, наконец, C лучше D.
Ответ: проект A — 1 место, проект B — 2 место, проект C — 3 место, проект D — 4 место. Наилучшим проектом является проект A.
Ранжирование>Принцип Борда
За первое место каждому проекту дадим 1 балл, за второе место — 2 балла, за третье — 3 балла и так далее. Далее подсчитаем количество баллов, которое получит каждый проект в сумме. Первое место в итоге получит проект, который наберет наименьшее число баллов, остальные места определятся сортировкой набранных баллов.
Итак, для нашего примера из табл. 34.4 получим следующее (см. табл. 36.9).
| Таблица 36.9. Распределение мест проектов методом Борда (пример) | ||||||||||||||||||||||||||||||
|
Ответ: проект A — 1 место (5 баллов), проект B — 2 место (9 баллов), проект C — 3 место (12 баллов), проект D — 4 место (14 баллов). Наилучшим проектом является проект A.
Ранжирование>Метод «Электра»
Рассмотрим данный метод на примере решения о покупке автомобиля.
Сначала составляют таблицу критериев, по которым будут оценивать проекты (см. табл. 36.10).
| Таблица 36.10. Таблица критериев для оценки проектов | |||||||||||||||||||||||||
|
Далее эксперт составляет таблицу оценок проектов (автомобилей). Например, для 7-ми автомобилей эксперт заполняет таблицу так, как показано в табл. 36.11.
| Таблица 36.11. Таблица оценок проектов по критериям | ||||||||||||||||||||||||||||||||||||||||||||||
|
Рассматриваем все пары проектов i и j. Если по какому-либо критерию i -ый проект лучше, чем j -ый, то соответствующий критерию вес прибавляется к Pij (эти баллы символизируют выбор «За»), в противном случае — к Nij (эти баллы символизируют выбор «Против»). То же самое справедливо для j -го проекта: если j -ый проект оказывается лучше, чем i -ый, то соответствующий критерию вес прибавляется к Pji, в противном случае — к Nji (обратите внимание на порядок следования индексов j и i у P и N). Если повстречалось одинаковое для i -го и для j -го проектов значение критерия, то оно пропускается. Затем, когда по паре i и j рассмотрены все критерии, находятся отношения Dij = Pij / Nij и Dji = Pji / Nji. Значения D ≤ 1 отбрасываются. Заметим, что Dji = 1/ Dij (и наоборот), таким образом, вычисления можно несколько упростить.
Рассмотрим, для примера, проекты 2 и 4 (i = 2, j = 4). По критерию «Цена» (вес критерия — 5 баллов) проект 2 хуже проекта 4; по критерию «Комфортность» (вес — 4 балла) проект 2 лучше проекта 4; по критерию «Скорость» (вес — 3 балла) проект 2 хуже проекта 4; по критерию «Дизайн» (вес — 3 балла) проект 2 лучше проекта 4. Таким образом, имеем:
P 24 = 0 + 4 + 0 + 3 = 7;
N 24 = 5 + 0 + 3 + 0 = 8;
D 24 = P 24/ N 24 =7/8 = 0.875 < 1 — отбрасываем;
P 42 = 5 + 0 + 3 + 0 = 8;
N 42 = 0 + 4 + 0 + 3 = 7;
D 42 = P 42/ N 42 =8/7 = 1/0.875 = 1.14 > 1 — принимаем.
Рассмотрим, для примера, проекты 1 и 2 (i = 1, j = 2). По критерию «Цена» проект 1 хуже проекта 2; по критерию «Комфортность» проекты 1 и 2 одинаковы, поэтому ничего не делаем; по критерию «Скорость» проект 1 лучше проекта 2; по критерию «Дизайн» проекты 1 и 2 одинаковы, поэтому ничего не делаем. Таким образом, имеем:
P 12 = 0 + 0 + 3 + 0 = 3;
N 12 = 5 + 0 + 0 + 0 = 5;
D 12 = P 12/ N 12 =3/5 = 0.6 < 1 — отбрасываем;
P 21 = 5 + 0 + 0 + 0 = 5;
N 21 = 0 + 0 + 3 + 0 = 3;
D 21 = P 21/ N 21 =5/3 = 1/0.6 = 1.67 > 1 — принимаем.
Все остальные пары рассчитываются аналогично.
Составляем матрицу, внося вычисленные (и принятые) значения D. Матрица имеет смысл предпочтений проектов между собой. Для нашего примера матрица выглядит следующим образом (см. табл. 36.12).
| Таблица 36.12. Полная матрица предпочтений проектов, составленная методом «Электра» | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задаемся порогом принятия решения, например C = 1.33, и оставляем в матрице те числа, которые больше или равны значению порога C. Таким образом, матрица разрежается (см. табл. 36.13).
| Таблица 36.13. Матрица предпочтений проектов при пороге C = 1.33 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
По матрице строится граф предпочтений (см. рис. 36.5). Из графа, построенного по табл. 36.13, видно, что проект 1 лучше проектов 4, 5, 7; проект 2 лучше проектов 1, 3, 7; проект 3 лучше проекта 7; проект 4 лучше проектов 3, 6, 7; проект 5 лучше проектов 3, 6, 7; проект 6 лучше проекта 2.
| |
| Рис. 36.5. Вид графа предпочтений для случая порога принятия решений C = 1.33 |
Очевидно, что решение не получено, так как в графе присутствуют петли. Например, 2 лучше 1, 1 лучше 5, 5 лучше 6, 6 лучше 2. Назначим порог отбора предпочтений C = 1.4 (это соответствует тому, что мы попробуем учесть только более сильные связи в графе, не отвлекаясь на малозначимые расхождения в проектах). Таким образом, матрица еще разрежается. В ней остаются только самые сильные связи (см. табл. 36.14).
| Таблица 36.14. Матрица предпочтений проектов при пороге C = 1.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
По матрице строится граф предпочтений (см. рис. 36.6). По графу и табл. 36.14 видно, что проект 1 лучше проектов 4, 5, 7; проект 2 лучше проектов 1, 7; проект 3 лучше проекта 7; проект 4 лучше проектов 3, 7; проект 5 лучше проектов 3, 7; проект 6 лучше проекта 2. Как видим из рис. 36.6, при C = 1.4 граф получился в таком виде, в котором он легко приводится к ЯПФ, следовательно, решение получено.
| |
| Рис. 36.6. Вид графа предпочтений для случая порога принятия решений C = 1.4 |
Петель в графе нет, при этом граф остался целостным. Решение говорит нам о том, что лучший проект — 6. На втором месте — проект 2, на третьем месте — проект 1, четвертое и пятое место делят проекты 4 и 5, на шестом месте — проект 3, на седьмом месте — проект 7.
Примечания
- Как можно видеть, порог C подбирается эмпирически. При малом пороге C (в матрице много компонент), в графе содержится много петель. Увеличивая порог C, можно добиться уменьшения количества связей и устранения малозначащих связей и петель. Однако нужно иметь в виду, что при очень высоком значении порога C граф распадется на несколько отдельных графов из-за отсутствия необходимых связей; в качестве иллюстрации см. рис. 36.7: при пороге C = 1.67 проекты 4 и 5 остаются без входящих стрелок, и поэтому становится неясно, какой же проект — 6-ой, 4-ый или 5-ый — является наилучшим. А при пороге C = 2 граф распадается на четыре не связанных подграфа.
- Если граф не будет найден ни при каких значениях порога C, то следует изменить веса критериев и всю процедуру провести снова.
- Если разумное изменение весов не помогает, и проекты все еще путаются (петли в графе), то надо детализировать проблему, добавив критерии.
| |
| Рис. 36.7. Вид графа предпочтений для случая порога принятия решений C = 1.67 (слева) и C = 2 (справа) |
 2017-12-14
2017-12-14 577
577