Приложение 1.
Нильс Бор в 1911 г. и независимо от него Ван-Лёвен в 1920 г., используя методы классической статистики, строго доказали следующую теорему.
В состоянии термодинамического равновесия система электрически заряженных частиц (электронов, атомных ядер и пр.), помещенная в постоянное магнитное поле, не может обладать магнитным моментом, если она строго подчиняется законам классической физики.
Такая система может быть намагничена только в неравновесном состоянии. При переходе в равновесное состояние намагничивание исчезает. Причина этого, вообще говоря, заключается в том, что постоянное магнитное поле, действуя на частицу с силой, перпендикулярной скорости, не может изменить кинетической энергии частицы. Т.о., в последовательной классической теории магнетизм должен отсутствовать.
Для объяснения магнетизма вещества требуется привлечение квантовых представлений.
Между тем, диамагнетизм и парамагнетизм были довольно успешно объяснены Ланжевеном, на первый взгляд, без использования квантовых представлений. В действительности же в классических теориях намагничивания молчаливо вводились представления сугубо квантового характера. Предполагалось, что из электрически заряженных частиц можно построить устойчивые образования – атомы и молекулы, объяснить существование которых под силу только квантовой механике. Другими словами, теория магнетизма в начале XX века строилась на основе представлений, которые мы называем полуклассическими.
Следует отметить, что несмотря на свою непоследовательность и недостаточность, полуклассическая теория, сохраняя наглядность изложения, позволяет в основном уяснить природу намагничивания.
Приложение 2.
Гиромагнитные эффекты.
Гиромагнитные отношения.
Согласно теории Бора момент количества орбитального движения электрона в атоме 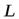 может принимать только дискретный ряд значений. В таком случае говорят, что момент квантуется.
может принимать только дискретный ряд значений. В таком случае говорят, что момент квантуется.
Допустимыми являются значения
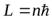 ,
,
где 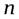 может принимать целочисленные значения, а
может принимать целочисленные значения, а 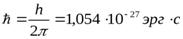 .
.
Вместе с механическим моментом магнитный момент орбитального движения также квантуется в соответствии с выражением
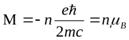 ,
,
где 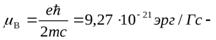 наименьшее значение магнитного момента атома, называемое магнетоном Бора.
наименьшее значение магнитного момента атома, называемое магнетоном Бора.
Тогда отношение магнитного момента и механического момента количества движения, обусловленных орбитальным движением электрона в атоме, равно
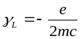 .
.
Спиновые механический и магнитный моменты.
Помимо орбитального электрон обладает также собственным, или спиновым, моментом количества движения (спином).
В стационарных состояниях проекция собственного момента количества движения электрона на выбранное направление может принимать только два значения:
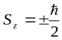 ;
;
Спину соответствует магнитный момент, проекция которого на выбранное направление равна магнетону Бора
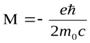 .
.
Т.о.. со спином связано гиромагнитное отношение
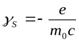 ,
,
которое вдвое больше орбитального.
Классическая физика не дает в этом случае правильного результата (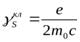 ), что свидетельствует лишь о непригодности используемой классической модели электрона.
), что свидетельствует лишь о непригодности используемой классической модели электрона.
Опыт Эйнштейна – де Гааза и эффект Барнетта.
Идея опыта Эйнштейна – де Гааза (1915г.) состоит в следующем.
Мысленно разобьем исследуемое вещество на две подсистемы: электронные оболочки атомов и кристаллическую решетку. Пусть магнитные свойства вещества обусловлены электронами атомных электронных оболочек. При намагничивании образца атомные магнитные моменты 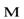 поворачиваются, стремясь сориентироваться вдоль вектора индукции
поворачиваются, стремясь сориентироваться вдоль вектора индукции 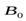 внешнего магнитного поля. Однако с магнитными моментами атомов
внешнего магнитного поля. Однако с магнитными моментами атомов 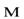 связаны механические моменты количества движения электронов оболочек атомов, равные
связаны механические моменты количества движения электронов оболочек атомов, равные 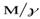 , которые также изменяются. Эти изменения механических моментов происходит за счет взаимодействий между атомами, т.е. внутренних сил, поэтому если система замкнута, то полный момент количества движения не может измениться и кристаллическая решетка должна получить такой же по величине, но противоположный по знаку механический момент (т.к. полный момент сохраняется).
, которые также изменяются. Эти изменения механических моментов происходит за счет взаимодействий между атомами, т.е. внутренних сил, поэтому если система замкнута, то полный момент количества движения не может измениться и кристаллическая решетка должна получить такой же по величине, но противоположный по знаку механический момент (т.к. полный момент сохраняется).
Следует заметить, что, в действительности, замкнутой является система «образец + намагничивающее поле в соленоиде». Однако, известно (понятно), что магнитное поле имеет относительно цилиндра момент количества движения, равный нулю, и поэтому не дает вклада в суммарный импульс системы.
Магнитный момент образца равен 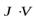 , где
, где 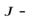 вектор намагничивания,
вектор намагничивания, 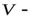 объем образца. Тогда, в результате намагничивания, момент количества движения электронных оболочек в веществе увеличивается на
объем образца. Тогда, в результате намагничивания, момент количества движения электронных оболочек в веществе увеличивается на 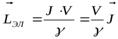 . Отсюда следует, что кристаллическая решетка образца должна получить такой же по величине момент количества движения, но противоположного знака, т.е.
. Отсюда следует, что кристаллическая решетка образца должна получить такой же по величине момент количества движения, но противоположного знака, т.е. 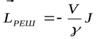 . Поэтому, если до намагничивания образец находился в состоянии покоя, то в результате намагничивания он должен прийти во вращение.
. Поэтому, если до намагничивания образец находился в состоянии покоя, то в результате намагничивания он должен прийти во вращение.
Если 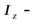 момент инерции тела, то
момент инерции тела, то 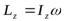 и угловая скорость
и угловая скорость 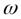 вращения тела может быть найдена из уравнения
вращения тела может быть найдена из уравнения 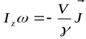 .
.
Опыт:
Небольшой железный цилиндрик подвешивался на тончайшей кварцевой нити и помещался внутрь
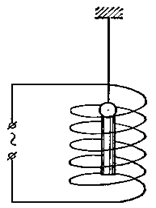 соленоида, в котором создавалось магнитное поле. Повороты цилиндрика
соленоида, в котором создавалось магнитное поле. Повороты цилиндрика
отмечались с помощью маленького зеркальца, скрепленного с ним. Оценим
величину эффекта.
Предположим, что цилиндр радиусом 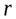 и массой
и массой 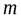 намагничивается до
намагничивается до
насыщения. Далее, пусть каждый атом в образце обладает магнитным
моментом, равным одному магнетону Бора 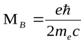 , тогда магнитный
, тогда магнитный
момент всего образца будет равен
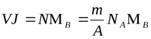 ,
,
где 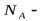 число Авогадро, а
число Авогадро, а 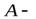 атомный вес.
атомный вес.
Принимая во внимание, что для цилиндра 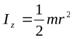 , получаем
, получаем
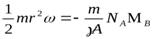 и
и 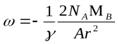 .
.
Для железного (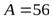 ) цилиндрика радиусом
) цилиндрика радиусом 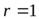 мм эта формула дает
мм эта формула дает 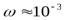 рад/c.
рад/c.
Эффект очень мал. Поэтому Эйнштейн и де Гааз, добиваясь усиления эффекта, пропускали по обмотке соленоида переменный ток. В переменном магнитном поле образец, периодически намагничиваясь и размагничиваясь, приходил в колебательное движение. Эффект усиливался, если частота изменения внешнего поля 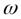 (частота переменного тока, изменяемая в опыте) совпадала с частотой собственных колебаний цилиндрика
(частота переменного тока, изменяемая в опыте) совпадала с частотой собственных колебаний цилиндрика 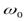 , т.е. наблюдалось явление резонанса.
, т.е. наблюдалось явление резонанса.
Уравнение крутильных колебаний цилиндрика записывается в виде
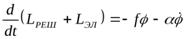 ,
,
где 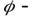 угол отклонения цилиндрика из положения равновесия;
угол отклонения цилиндрика из положения равновесия; 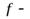 модуль кручения нити;
модуль кручения нити; 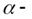 постоянная, учитывающая сопротивление воздуха и прочие тормозящие силы, которые предполагаются пропорциональными скорости.
постоянная, учитывающая сопротивление воздуха и прочие тормозящие силы, которые предполагаются пропорциональными скорости.
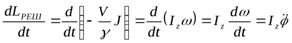 ;
;
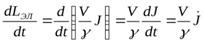 .
.
Поэтому уравнение принимает вид:
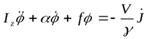 ,
,
если теперь ввести частоту собственных колебаний как 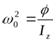 и коэффициент затухания
и коэффициент затухания 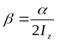 , то получаем
, то получаем
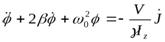 .
.
Это уравнение вынужденных крутильных колебаний. Величина, стоящая в правой части уравнения играет роль вынуждающей силы. Она возникает в результате намагничивания и перемагничивания цилиндрика и предполагается известной. Поскольку связь между намагниченностью и вызывающим её полем нелинейна (железо – ферромагнетик), то правую часть уравнения раскладывают в ряд Фурье, сохраняя в этом разложении для нахождения решения вблизи резонанса только член с основной частотой 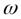 (Сивухин, т.3, §
(Сивухин, т.3, § 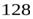 ).
).
Исследование крутильных колебаний позволяет определить гиромагнитное отношение для материала образца. Для железного образца было получено 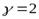 , которое означает, что ферромагнетизм железа определяется спиновым магнетизмом электронов.
, которое означает, что ферромагнетизм железа определяется спиновым магнетизмом электронов.
Эффект Барнетта (1909 г.).
Существует явление, обратное магнитомеханическому. Оно заключается в том, что при вращении парамагнитные тела намагничиваются, и называется гиромагнитным.
Объяснить этот эффект можно следующим образом. При внесении в магнитное поле электронная оболочка атома приходит во вращение относительно кристаллической решетки с угловой скоростью 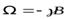 . При наличии такого относительного движения столкновения между атомами приводят к намагничиванию среды. Поскольку движение относительное, то следует ожидать такого же намагничивания, если привести во вращение решетку с угловой скоростью
. При наличии такого относительного движения столкновения между атомами приводят к намагничиванию среды. Поскольку движение относительное, то следует ожидать такого же намагничивания, если привести во вращение решетку с угловой скоростью 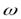 , равной по величине, но противоположно направленной скорости
, равной по величине, но противоположно направленной скорости 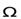 . Другими словами, вращение тела с угловой скоростью
. Другими словами, вращение тела с угловой скоростью 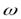 вызывает то же намагничивание, что и магнитное поле
вызывает то же намагничивание, что и магнитное поле 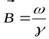 .
.
Это явление наблюдалось Барнеттом в 1909 (1914) г.
Сделаем численную оценку величины этого эффекта, допустив, что гиромагнитное отношение связано с орбитальным движением электронов (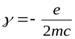 ), и задав скорость вращения, равной 100 об/с.
), и задав скорость вращения, равной 100 об/с.
(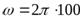 рад/с):
рад/с): 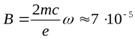 Гс.
Гс.
Для сравнения, магнитное поле у поверхности Земли составляет 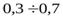 Гс.
Гс.
Исследования магнитомеханического и гиромагнитного явлений показали, что гиромагнитное отношение 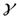 всегда отрицательно. Тем самым было подтверждено, что магнетизм обусловлен движением отрицательных электрических зарядов (электронов). Численные значения величины
всегда отрицательно. Тем самым было подтверждено, что магнетизм обусловлен движением отрицательных электрических зарядов (электронов). Численные значения величины 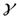 оказались заключенными в пределах от
оказались заключенными в пределах от 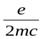 до
до 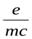 . Весьма важно, что для всех исследованных ферромагнетиков (железо, никель, кобальт, ряд сплавов) гиромагнитное отношение оказалось равным
. Весьма важно, что для всех исследованных ферромагнетиков (железо, никель, кобальт, ряд сплавов) гиромагнитное отношение оказалось равным 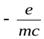 . Это показывает, что магнетизм ферромагнетиков обусловлен только спином электронов, но не их орбитальным движением.
. Это показывает, что магнетизм ферромагнетиков обусловлен только спином электронов, но не их орбитальным движением.
Опыт Штерна-Герлаха. 
Наглядное и непосредственное доказательство наличия у электрона собственного магнитного момента было получено немецкими физиками О. Штерном (O.Stern) и В. Герлахом (W.Gerlach) в опытах, поставленных ими в 1922 г.
В вакууммированной установке исследовалось прохождение узкого пучка атомов серебра (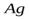 ), двигавшихся в направлении оси
), двигавшихся в направлении оси 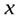 , в сильно неоднородном (вдоль оси
, в сильно неоднородном (вдоль оси 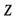 ) магнитном поле. В таком поле
) магнитном поле. В таком поле
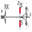 атомы, обладающие магнитным моментом,
атомы, обладающие магнитным моментом,
должны отклоняться от направления их
первоначального распространения.
На атом с магнитным моментом 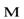 в
в
неоднородном магнитном поле 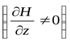 .
.
действует сила, равная 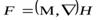 .
.
Если магнитный момент атома 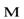 направлен под углом
направлен под углом 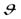 к оси
к оси 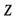 , то
, то
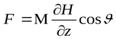 .
.
Под влиянием этой силы атом будет отклоняться в направлении оси 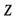 на величину
на величину
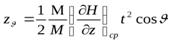 ,
,
где 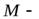 масса атома;
масса атома; 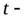 время пролета в магнитном в поле (
время пролета в магнитном в поле (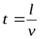 ,
, 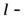 длина магнита,
длина магнита, 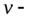 скорость атомов вдоль оси
скорость атомов вдоль оси 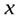 ).
).
Если бы все значения углов 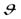 были бы равновероятны, то при включении магнитного поля на экране
были бы равновероятны, то при включении магнитного поля на экране
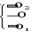
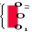 вместо сфокусированного в (
вместо сфокусированного в ( )
) 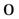 изображения получили бы широкую полосу в
изображения получили бы широкую полосу в
пределах от 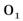 до
до 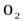 .
. 
Однако в опыте Штерна – Герлаха атомный пучок расщеплялся на две
компоненты, симметрично расположенные относительно первоначального
направления. Это означает, что атомы пучка обладают магнитным моментом
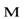 , проекция которого
, проекция которого 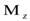 в поле
в поле 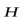 принимает два значения
принимает два значения 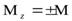 .
.
Это согласуется с теоретической формулой 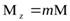 пространственного
пространственного
квантования проекции магнитного момента атома на направление внешнего магнитного поля 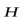 при
при 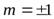 .
.
В опыте Штерна – Герлаха использовались атомы серебра в основном состоянии, во внешней электронной оболочке которого находится один электрон. Это означает, что магнитный момент атома может быть связан только с существованием собственного магнитного момента электрона.
Опыт Штерна – Герлаха и другие, более ранние эксперименты привели Уленбека и Гаудсмита (1925г.) к гипотезе существования у электрона собственного механического момента – спина.
Приложение 3.
Рассмотрим, какие же силы сообщают атому ларморовское вращение. В момент включения магнитного поля возникает вихревое электрическое поле:
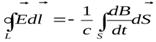 .
.
Если магнитное поле включается адиабатически (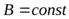 за время одного оборота), то можно написать
за время одного оборота), то можно написать
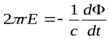 ,
,
откуда
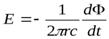 .
.
Тогда момент силы, действующей на электрон, движущийся по орбите радиусом 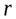 , определяется как
, определяется как
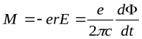 .
.
Теперь уравнение моментов принимает вид
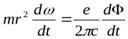 .
.
Если при 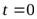
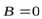 , то, интегрируя, получаем
, то, интегрируя, получаем
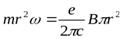 ,
,
откуда
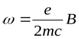 .
.
Если изменение поля прекратить, то 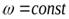
Магнитное взаимодействие
Атомно-силовой микроскоп может использоваться для исследования магнитных полей на поверхности образца. Такие методики объединяются под названием МСМ (магнитно-силовая микроскопия). В них используются специальные кантилеверы, которые покрыты магнитной пленкой. При взаимодействии с магнитным полем образца такойкантилевер отклоняется. Могут существовать следующие типы кантилеверов: диамагнитные, парамагнитные [ 1 ], суперпарамагнитные [ 2 ] и ферромагнитные (магнитожесткие [ 3 ] и магнитомягкие [ 4 ]).
Здесь мы кратко напомним об этих трех типах магнетиков, рассмотрев диамагнетизм, парамагнетизм и ферромагнетизм на феноменологическом уровне. Заинтересованных же отошлем к более серьезной литературе, например, [ 5, 6, 7 ].
Магнитные свойства вещества описываются вектором намагниченности 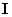 . Его связь с напряженностью магнитного поля
. Его связь с напряженностью магнитного поля  задается формулой [ 8,9 ]:
задается формулой [ 8,9 ]:
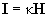 | (1) |
где 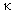 – магнитная восприимчивость вещества. В свою очередь, напряженность магнитного поля связана с вектором магнитной индукции
– магнитная восприимчивость вещества. В свою очередь, напряженность магнитного поля связана с вектором магнитной индукции 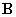 и вектором намагничивания следующим образом:
и вектором намагничивания следующим образом:
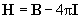 | (2) |
Подставляя (1) в (2), получим:
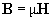 | (3) |
где 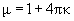 – магнитная проницаемость вещества. Таким образом, магнитные свойства вещества описываются одним независимым параметром –
– магнитная проницаемость вещества. Таким образом, магнитные свойства вещества описываются одним независимым параметром – 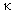 или
или 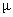 .
.
Диа- и парамагнетизм.
Атомы многих веществ не имеют постоянных магнитных моментов, или, вернее, все спиновые и орбитальные магнитные моменты внутри атома уравновешены так, что суммарный магнитный момент равен нулю. Если наложить магнитное поле, то внутри атома будут генерироваться слабые дополнительные токи. В соответствии с законом Ленца они будут индицироваться так, чтобы уменьшить магнитное поле, и наведенный магнитный момент атомов направлен навстречу магнитному полю. Таков механизм диамагнетизма.
Магнитная восприимчивость и магнитная проницаемость для диамагнетиков:
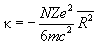 | (4) |
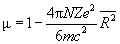 | (5) |
где 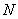 – число атомов в единице объема,
– число атомов в единице объема, 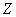 – число электронов в атоме,
– число электронов в атоме, 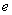 и
и 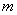 – заряд и масса электрона,
– заряд и масса электрона, 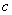 – скорость света,
– скорость света, 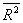 – средний квадрат расстояния электрона до ядра. Энергия теплового движения слишком мала, чтобы изменить внутреннее (квантованное) состояние атома. Поэтому для диамагнетиков
– средний квадрат расстояния электрона до ядра. Энергия теплового движения слишком мала, чтобы изменить внутреннее (квантованное) состояние атома. Поэтому для диамагнетиков 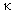 и
и 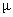 не должны зависеть от температуры. Обратим внимание, что
не должны зависеть от температуры. Обратим внимание, что 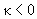 и, тем самым,
и, тем самым, 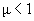 .
.
К диамагнетикам относятся, например, кислород, алюминий, платина, хлористое железо – 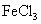 , благородные газы и т.д.
, благородные газы и т.д.
Однако существуют такие вещества, атомы которых обладают магнитным моментом, спиновым или орбитальным. Таким образом, кроме диамагнитного эффекта (а он всегда присутствует) есть возможность выстраивания индивидуальных атомных моментов в одном направлении. Магнитные моменты ориентируются в направлении магнитного поля, усиливая его.
Парамагнетизм, вообще говоря, довольно слаб, потому что выстраивающие силы относительно малы по сравнению с силами теплового движения, которые стараются разрушить упорядочивание. Отсюда следует, что парамагнетизм особо чувствителен к температуре. Эффект парамагнетизма тем сильнее, чем ниже температура.
Пусть 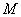 – магнитный момент атома,
– магнитный момент атома, 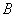 – магнитная индукция,
– магнитная индукция, 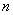 – число атомов в единице объема,
– число атомов в единице объема, 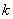 – константа Больцмана,
– константа Больцмана, 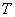 – температура. Тогда для парамагнетиков в слабых полях –
– температура. Тогда для парамагнетиков в слабых полях – 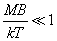 , когда зависимость вектора намагничивания от напряженности магнитного поля линейна, магнитная восприимчивость и магнитная проницаемость равны:
, когда зависимость вектора намагничивания от напряженности магнитного поля линейна, магнитная восприимчивость и магнитная проницаемость равны:
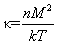 | (6) |
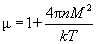 | (7) |
Обратно пропорциональная зависимость восприимчивости от абсолютной температуры (6) носит название закона Кюри. Заметим, что для парамагнетиков 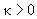 и, тем самым,
и, тем самым, 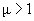 .
.
В сильных полях намагничивание приходит в состояние насыщение, когда все магнитные моменты устанавливаются параллельно полю:
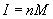 | (8) |
Так как диамагнетизм проявляется во всех веществах, он частично или полностью компенсирует парамагнетизм за счет противоположного по знаку вклада в восприимчивость. Поэтому для материалов с атомами, имеющими магнитный момент, можно говорить лишь о преобладании диа- или парамагнитных свойств в веществе, причем их баланс зависит от температуры. К парамагнетикам относятся, например, азот, углекислота, вода, серебро, висмут и т.д.
Ферромагнетизм.
В ферромагнетиках эффект упорядочения магнитных моментов проявляется во много раз сильнее, чем в диа- и парамагнетиках. Ферромагнетизм определяется коллективным взаимодействием атомных магнитных моментов, находящимися в состоянии с нарушенной симметрией (фазовый переход второго рода) и образующих магнитные домены. Ферромагнетиками называются тела, которые могут обладать спонтанной намагниченностью, то есть намагничены уже в отсутствие магнитного поля. Типичными представителями ферромагнетиков являются переходные металлы: железо, кобальт, никель и многие их сплавы. Ферромагнетизмом обладают некоторые редкоземельные элементы (гадолиний, тербий, диспрозий, гольмий, эрбий, туллий).
Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между 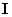 и
и  или между
или между 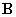 и
и  . Характер этой зависимости представлен на рис. 1 и 2.
. Характер этой зависимости представлен на рис. 1 и 2.
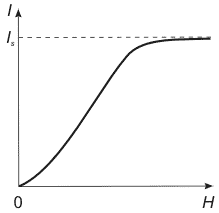 | 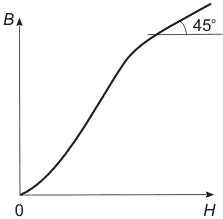 |
| Рис. 1. Зависимость намагничивания от напряженности магнитного поля. | Рис. 2. Зависимость магнитной индукции от напряженности магнитного поля. |
По мере возрастания  намагниченность
намагниченность 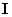 сначала быстро увеличивается, а затем приходит к насыщению и остается практически постоянной:
сначала быстро увеличивается, а затем приходит к насыщению и остается практически постоянной: 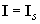 (насыщение), то есть кривая
(насыщение), то есть кривая 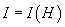 переходит в горизонтальную прямую. Магнитная индукция
переходит в горизонтальную прямую. Магнитная индукция 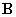 также растет с увеличением поля
также растет с увеличением поля  , а в состоянии насыщения
, а в состоянии насыщения 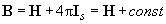 , то есть кривая
, то есть кривая 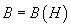 переходит в прямую, наклоненную под углом
переходит в прямую, наклоненную под углом 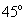 (если
(если 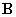 и
и  откладывать на осях координат в одинаковом масштабе).
откладывать на осях координат в одинаковом масштабе).
Магнитная восприимчивость 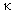 и магнитная проницаемость
и магнитная проницаемость 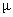 уже зависят не только от свойств вещества и температуры, как у диа- и парамагнетиков, а являются функциями напряженности поля
уже зависят не только от свойств вещества и температуры, как у диа- и парамагнетиков, а являются функциями напряженности поля 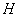 и, более того, определяется его историей.
и, более того, определяется его историей.
Восприимчивость и проницаемость сначала возрастают с 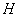 , затем проходят через максимум, и, наконец, в сильных полях, когда достигнуто насыщение,
, затем проходят через максимум, и, наконец, в сильных полях, когда достигнуто насыщение, 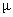 стремится к единице (рис.3), а
стремится к единице (рис.3), а 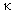 – к нулю.
– к нулю.
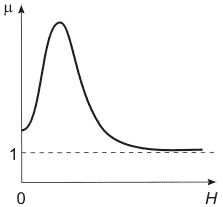 |
| Рис. 3. Зависимость магнитной восприимчивости от напряженности магнитного поля. |
Значения 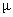 в максимуме у большинства ферромагнетиков при обычных температурах составляют многие сотни и тысячи единиц.
в максимуме у большинства ферромагнетиков при обычных температурах составляют многие сотни и тысячи единиц.
Вторая характерная особенность ферромагнетиков состоит в том, что для них зависимость 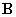 от
от  или
или 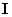 от
от  не однозначна, а определяется предшествующей историей намагничивания ферромагнитного образца. Это явление называется магнитным гистерезисом. Изображенная на рисунке 4 замкнутая кривая
не однозначна, а определяется предшествующей историей намагничивания ферромагнитного образца. Это явление называется магнитным гистерезисом. Изображенная на рисунке 4 замкнутая кривая 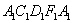 называется петлей гистерезиса, а кривая
называется петлей гистерезиса, а кривая 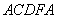 – предельной (наибольшей) петлей гистерезиса.
– предельной (наибольшей) петлей гистерезиса.
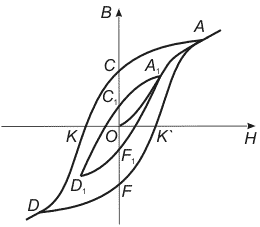 |
| Рис. 4. Петля гистерезиса. |
При 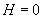 индукция
индукция 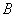 не обращается в нуль, а изображается отрезком
не обращается в нуль, а изображается отрезком 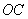 . Ему соответствует остаточное намагничивание
. Ему соответствует остаточное намагничивание 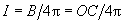 . С наличием такого остаточного намагничивания связано существование постоянных магнитов. Для того, чтобы размагнитить образец, надо довести кривую размагничивания до точки
. С наличием такого остаточного намагничивания связано существование постоянных магнитов. Для того, чтобы размагнитить образец, надо довести кривую размагничивания до точки 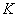 или
или 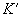 . Этим точкам соответствует магнитное поле
. Этим точкам соответствует магнитное поле 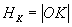 . Оно называется коэрцитивной силой ферромагнетика. Значения остаточного намагничивания и коэрцитивной силы для разных ферромагнетиков меняются в широких пределах. Для мягкого железа петля гистерезиса узкая (коэрцитивная сила мала), для стали и всех материалов, идущих на изготовление магнитов, – широкая (коэрцитивная сила велика). Например, для кобальта и его сплавов, которые используются для покрытия магнитожесткихкантилеверов, характерная величина коэрцитивной силы составляет 400 эрстед. С другой стороны, магнитное поле зонда в целом ряде случаев может оказаться слишком большим, что может приводить к искажению или даже разрушению исследуемой магнитной структуры. Для этих целей используют зонды с покрытием
. Оно называется коэрцитивной силой ферромагнетика. Значения остаточного намагничивания и коэрцитивной силы для разных ферромагнетиков меняются в широких пределах. Для мягкого железа петля гистерезиса узкая (коэрцитивная сила мала), для стали и всех материалов, идущих на изготовление магнитов, – широкая (коэрцитивная сила велика). Например, для кобальта и его сплавов, которые используются для покрытия магнитожесткихкантилеверов, характерная величина коэрцитивной силы составляет 400 эрстед. С другой стороны, магнитное поле зонда в целом ряде случаев может оказаться слишком большим, что может приводить к искажению или даже разрушению исследуемой магнитной структуры. Для этих целей используют зонды с покрытием 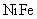 –
– 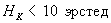 . Совершенно такой же характер имеет петля гистерезиса, когда по вертикальной оси откладывается не индукция
. Совершенно такой же характер имеет петля гистерезиса, когда по вертикальной оси откладывается не индукция 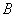 , а намагничивание
, а намагничивание 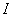 .
.
Выводы.
· Вещества по их поведению в магнитном поле подразделяют на три основных типа: диамагнитные, парамагнитные и ферромагнитные.
· Диамагнитные свойства проявляют все вещества. Суть эффекта – в возникновении индуцированных внутриатомных токов, которые уменьшают индукцию магнитного поля в веществе. Магнитная восприимчивость диамагнетиков отрицательна.
· Парамагнитные свойства могут проявлять вещества с атомами, имеющими магнитный момент. Магнитная восприимчивость при этом положительна и уменьшается с ростом температуры.
· Ферромагнетизм является очень сильным коллективным эффектом. Причем магнитная восприимчивость и проницаемость вещества становится неоднозначными функциями поля и зависят от его истории. Характерные ферромагнитные явления – спонтанная намагниченность и гистерезис намагниченности. Коэрцитивная сила магнитожесткихкантилеверов (с кобальтовым покрытием) составляет порядка 400 эрстед, а магнитомягких (с покрытием 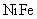 ) – менее 10 эрстед.
) – менее 10 эрстед.
Магнитное поле в веществе. Намагничивание вещества. Вектор намагниченности. Магнитная проницаемость и магнитная восприимчивость. Диа- пара- и ферромагнетики.
Всякое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться).
Намагниченное поле создаёт магнитное поле 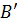 , которое накладывается на обусловленное токами поле
, которое накладывается на обусловленное токами поле 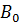 . Оба поля в сумме дают результирующее поле
. Оба поля в сумме дают результирующее поле 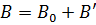 .
.
Макроток – ток, текущий по проводнику в вакууме.
Микроток возникает в результате движения электронов вокруг ядра атома.
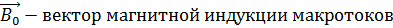
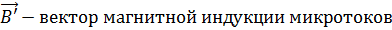
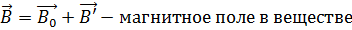
Намагничение магнетика характеризуют магнитным моментом единицы объёма, эту величину называют намагниченностью J.
где 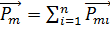 – магнитный момент
– магнитный момент
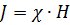
Намагниченность магнетика пропорциональна напряжённости поля.
χ - магнитная восприимчивость.
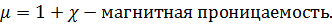
В зависимости от знака и величины магнитной восприимчивости χ все магнетики подразделяются на три группы:
1) диамагнетики
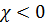 и мала по абсолютной величине
и мала по абсолютной величине 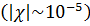
Атомы не обладают магнитным моментом 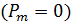 в отсутствии внешнего магнитного поля. Во внешнем магнитном поле намагничиваются против направления поля. Под действием внешнего магнитного поля происходит прецессия электронных орбит, в результате у диамагнетика появляется индуцированный магнитный момент атома, направленный против внешнего поля.
в отсутствии внешнего магнитного поля. Во внешнем магнитном поле намагничиваются против направления поля. Под действием внешнего магнитного поля происходит прецессия электронных орбит, в результате у диамагнетика появляется индуцированный магнитный момент атома, направленный против внешнего поля.
К диамагнетикам принадлежат золото, серебро, медь, инертные газы.
Являются слабомагнитными веществами. Намагниченность изменяется с напряжённостью поля линейно.
2) парамагнетики
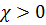 и тоже невелика
и тоже невелика 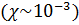
Магнитный момент атомов 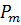 отличен от нуля в отсутствии внешнего поля. Во внешнем магнитном поле намагничиваются параллельно полю, магнитные моменты атомов разворачиваются к полю.
отличен от нуля в отсутствии внешнего поля. Во внешнем магнитном поле намагничиваются параллельно полю, магнитные моменты атомов разворачиваются к полю.
Являются слабомагнитными веществами. Намагниченность изменяется с напряжённостью поля линейно.
3) ферромагнетики
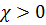 и достигает больших значений
и достигает больших значений 
Способны обладать намагниченностью в отсутствие внешнего магнитного поля.
К ферромагнетикам принадлежат железо, никель, кобальт.
Являются сильномагнитными веществами. Намагниченность зависит от напряженности сложным образом.
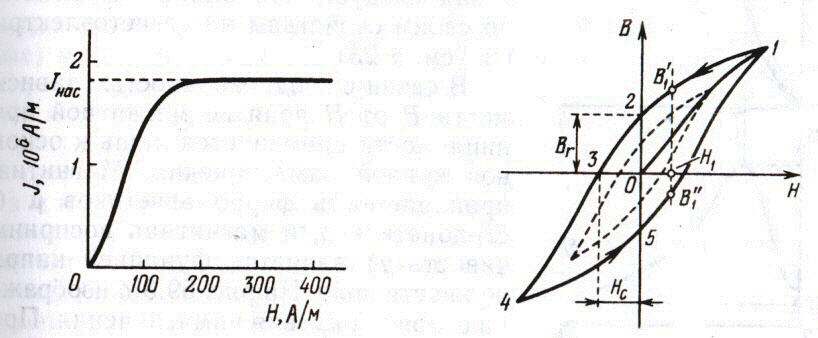
Основная кривая намагничения на диаграмме J-H.
Намагниченность J достигает насыщения в полях порядка 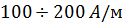 .
.
Основная диаграмма намагничения на диаграмме В-Н.
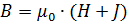
По достижении насыщения B продолжает расти.
Для ферромагнетиков характерно наличие гистерезиса. При действии на ферромагнетик переменного магнитного поля индукция изменяется в соответствии с кривой 1-2-3-4-5-1, которая называется петлёй гистерезиса.
Если довести намагничение до насыщения (точка1) и затем уменьшать напряжённость магнитного поля, то индукция B изменяется по кривой 1-2. В точке 2 (Н=0) намагничение не исчезает. 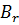 – остаточная индукция. Намагниченность имеет при этом значение
– остаточная индукция. Намагниченность имеет при этом значение 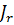 , называемое остаточной намагниченностью. Индукция B обращается в нуль под действием поля
, называемое остаточной намагниченностью. Индукция B обращается в нуль под действием поля 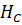 , имеющего направление, противоположное полю, вызвавшему намагничение. Напряжённость
, имеющего направление, противоположное полю, вызвавшему намагничение. Напряжённость 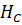 называется коэрцитивной силой.
называется коэрцитивной силой.
Если 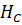 велика, ферромагнетик называется жёстким, для него характерна широкая петля гистерезиса. Ферромагнетик с малой
велика, ферромагнетик называется жёстким, для него характерна широкая петля гистерезиса. Ферромагнетик с малой 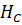 называется мягким (узкая петля гистерезиса).
называется мягким (узкая петля гистерезиса).
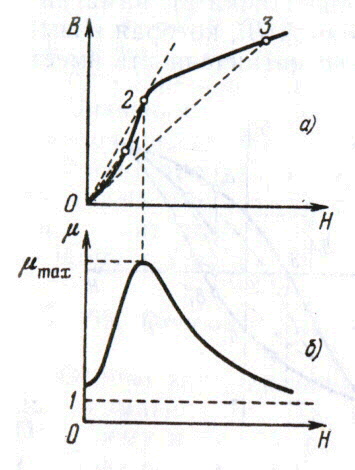
График зависимости μ от Н (рис.б).
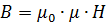
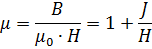
Максимальное значение проницаемости достигается несколько раньше, чем насыщение. При неограниченном возрастании Н проницаемость приближается к единице.
Для каждого ферромагнетика имеется определённая температура 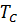 , при которой вещество утрачивает ферромагнитные свойства. Эта температура называется точкой Кюри.
, при которой вещество утрачивает ферромагнитные свойства. Эта температура называется точкой Кюри.
Для железа 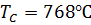 , для никеля
, для никеля 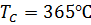 . При температуре выше точки Кюри ферромагнетик становится парамагнетиком.
. При температуре выше точки Кюри ферромагнетик становится парамагнетиком.
 2017-12-14
2017-12-14 3291
3291