Основные определения и формулы
Натуральные числа: 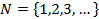
| Простые | Составные | 1 (единица) |
| имеют только два делителя: 1 и само число: 2, 3, 5, 7, … | имеют больше двух делителей: 4, 6, 8, … | не является ни простым ни составным числом |
Целые числа: 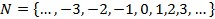
Рациональные числа: числа, представляемые в виде дроби  , где
, где 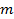 – целое число, а
– целое число, а  – натуральное.
– натуральное.
| Основное свойство дроби | Сложение и вычитание дробей | Умножение дробей | Деление дробей |
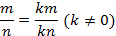
| 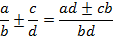
| 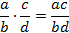

| 
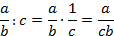
|
Десятичная дробь, у которой начиная с некоторого знака после запятой повторяются цифры или группы цифр (период дроби) – бесконечная периодическая.
· Если период такой дроби начинается сразу после запятой, то для представления ее в виде обыкновенной дроби необходимо в числителе записать период дроби, а в знаменателе число, записанное таким количеством девяток, сколько цифр в периоде.
· Если между запятой и периодом дроби есть еще цифры, то числитель дроби равен разности между самим числом, включая один период, и числом, стоящим до периода, а знаменатель – число, записанное таким количеством девяток, сколько цифр в периоде и таким количеством нулей, сколько цифр после запятой до периода.
Например:

Иррациональными числами называют бесконечные десятичные непериодические дроби. Примерами таких чисел являются 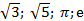 и другие.
и другие.
Множество всех рациональных и иррациональных чисел – множество действительных чисел.
Для любого числа  существует противоположное ему число существует противоположное ему число 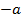 : :
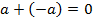
| Для любого числа 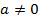 существуетобратное ему число существуетобратное ему число 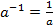 : :

|
 2017-12-14
2017-12-14 762
762






