Система линейных алгебраических уравнений
При записи систем линейных уравнений применяются следующие обозначения: переменные обозначаются буквой x с индексом, который указывает номер переменной, коэффициенты при переменной обозначаются буквой a с двумя индексами: первый индекс указывает номер уравнения, второй ˗ номер переменной. Свободные члены снабжаются также двумя индексами.
Система n линейных алгебраических уравнений с n переменными запишется следующим образом:
 (1)
(1)
Решением системы (1) называется совокупность таких значений переменных  при подстановке которых в данную систему каждое уравнение системы обращается в истинное числовое равенство.
при подстановке которых в данную систему каждое уравнение системы обращается в истинное числовое равенство.
Описание метода Гаусса для частного случая
Метод Гаусса является одним из распространенных методов решений систем линейных уравнений. В основе метода лежит приём последовательного исключения переменных для получения эквивалентной треугольной или трапецеидальной системы уравнений. Сущность метода проиллюстрируем на системе трёх линейных уравнений с тремя переменными:
 (2)
(2)
Пусть 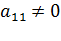 (в противном случае переставим уравнения так, чтобы это условие выполнялось). Разделив коэффициенты первого уравнения системы (3) на
(в противном случае переставим уравнения так, чтобы это условие выполнялось). Разделив коэффициенты первого уравнения системы (3) на  , получим уравнение:
, получим уравнение:

Обозначим 
или

Тогда уравнение (3) примет вид:

Исключим переменную  из второго и третьего уранений системы (2). Чтобы исключить переменную
из второго и третьего уранений системы (2). Чтобы исключить переменную  из второго уравнения системы, нужно из этого уравнения вычесть уравнение (4), умноженное на
из второго уравнения системы, нужно из этого уравнения вычесть уравнение (4), умноженное на  :
:
– 
_____________________________________________________________ (5)
 т.е.
т.е.
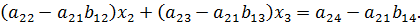
Обозначим  ,
,  ,
,  ,
,
Или 
Уравнение (5) примет вид:
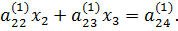 (6)
(6)
Для исключения переменной  из третьего уравнения системы (2) вычтем из этого уравнения уравнение (4), умноженное на
из третьего уравнения системы (2) вычтем из этого уравнения уравнение (4), умноженное на  В результате получим:
В результате получим:

Обозначив  , перепишем полученное уравнение в виде:
, перепишем полученное уравнение в виде:
 .
.
В результате проведённых эквивалентных преобразований получим систему линейных уравнений:

Разделив коэффициенты второго уравнения системы (7) на  , получим уравнение:
, получим уравнение:

где 
Исключим 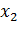 из третьего уравнения системы (7). Для этого вычтем из него уравнение (8), умноженное на
из третьего уравнения системы (7). Для этого вычтем из него уравнение (8), умноженное на  . Получим:
. Получим:
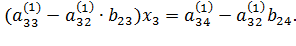
Обозначив  , перепишем уравнение в виде:
, перепишем уравнение в виде:  . Если
. Если  , то разделив полученное уравнение на
, то разделив полученное уравнение на  , получим уравнение:
, получим уравнение:
 где
где  .
.
Таким образом, в результате преобразований получена система трёх уравнений:

Если  , то имеем систему:
, то имеем систему:

В случае  система (10) и, следовательно, система (2) не имеют решений. Если
система (10) и, следовательно, система (2) не имеют решений. Если 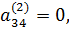 то третье уравнение, имеющее вид
то третье уравнение, имеющее вид 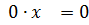 , исключаем и получаем трапецеидальную систему:
, исключаем и получаем трапецеидальную систему:

 2017-12-14
2017-12-14 685
685







