Дифференциальное исчисление

 

ЗАДАНИЕ № 1

Найти производную функции.

 

1.а)	б)		2.а)	б)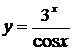
3.а)	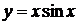б)		4.а)	б)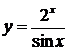
5.а)	б)		6.а)	б)
7.а)	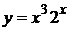б)		8.а)	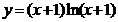б)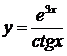
9.а)	б)		10.а)	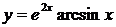б)
11.а)	б)	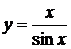	12.а)	б)
13.а)	б)		14.а)	б)
15.а)	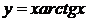б)		16.а)	б)
17.а)	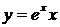б)		18.а)	б)
19.а)	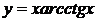б)		20.а)	б)
21.а)	б)		22.а)	б)
23.а)	б)		24.а)	б)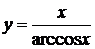
25.а)	б)		26.а)	б)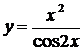
27.а)	б)	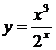	28.а)	б)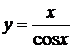
29.а)	б)		30.а)	б)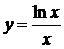

 

ЗАДАНИЕ № 2

Найти производную сложной функции.

 

1.а)	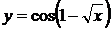б)
2.а)	б)
3.а)	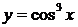б)
4.а)	б)
5.а)	б)
6.а)	б)
7.а)	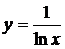б)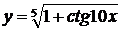
8.а)	б)
9.а)	б)
10.а)	б)
11.а)	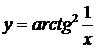б)
12.а)	б)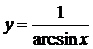
13.а)	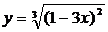б)
14.а)	б)
15.а)	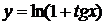б)
16.а)	б)
17.а)	б)
18.а)	б)
19.а)	б)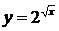
20.а)	б)
21.а)	б)
22.а)	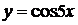б)
23.а)	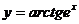б)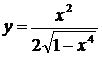
24.а)	б)
25.а)	б)
26.а)	б)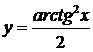
27.а)	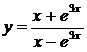б)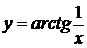
28.а)	б)
29.а)	б)
30.а)	б)

 

 

ЗАДАНИЕ № 3

Найти производную функций, используя логарифмическое дифференцирование.

 

1. а)	б)
2. а)	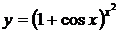б)
3. а)	б)
4. а)	б)
5. а)	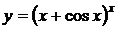б)
6. а)	б)
7. а)	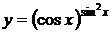б)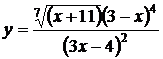
8. а)	б)
9. а)	б)
10. а)	б)
11. а)	б)
12. а)	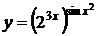б)
13. а)	б)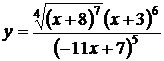
14. а)	б)
15. а)	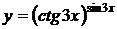б)
16. а)	б)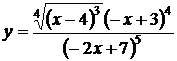
17. а)	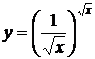б)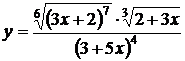

 

 

ЗАДАНИЕ № 4

Найти первую производную функции, заданной параметрически.

 

1.	2.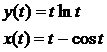
3.	4.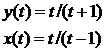
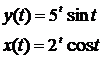
5.	6.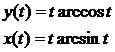
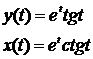
7.	8.
9.	10.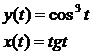
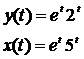
11.	12.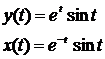
13.	14.
15.	16.
17.	18.
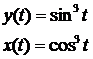
19.	20.
21.	22.
23.	24.
25.	26.
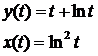
27.	28.
29.	30.

 

 

ЗАДАНИЕ № 5

Найти пределы, используя правило Лопиталя.

 

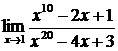
1.	2.
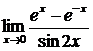
3.	4.
5.	6.
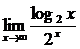
7.	8.
9.	10.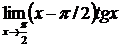
11.	12.
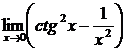
13.	14.
15.	16.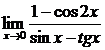
17.	18.
19.	20.
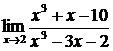
21.	22.
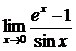
23.	24.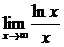
25.	26.
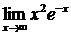
27.	28.
29.	30.

 

ЗАДАНИЕ № 6

Найти уравнение касательной к функции в заданной точке М.

 

1.	2.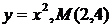
3.	4.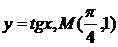
5.	6.
7.	8.
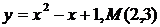
9.	10.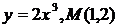
11.	12.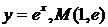
13.	14.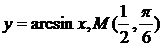
15.	16.
17.	18.
19.	20.
21.	22.
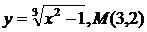
23.	24.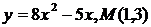
25.	26.
27.	28.
29.	30.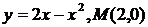

 

 

ЗАДАНИЕ № 7

Вычислить приближенно с помощью дифференциала.

 

1. , .

2. , .

3. , .

4. , .

5. , .

6. , .

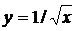7. ,

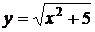8. ,

9. , .

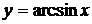10. , .

11. , .

12. .

13. , .

14. , .

15. , .

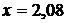16. , .

17. , .

 

 

ЗАДАНИЕ № 8

 

Найти производную функции указанного порядка.

1.	2.
3.	4.
5.	6.
7.	8.
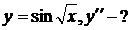
9.	10.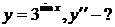
11.	12.
13.	14.
15.	16.
17.	18.
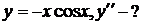
19.	20.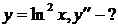
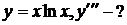
21.	22.
23.	24.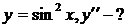
25.	26.
27.	28.
29.	30.

 

 

ЗАДАНИЕ № 9

Построить график функции.

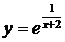
1.	2.
3.	4.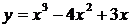
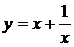
5.	6.
7.	8.
9.	10.
11.	12.
13.	14.
15.	16.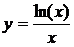
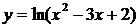
17.	18.
19.	20.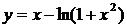
21.	22.
23.	24.
25.	26.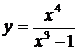
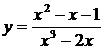
27.	28.
29.	30.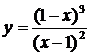

 

 

Пример решения задачи №1.

Найти производную функции: а) 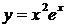б)

Решение: а) В соответствии с правилом нахождения производной произведения получаем

б) В соответствии с правилом нахождения производной частного получаем

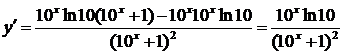
Ответ: а) б)

Пример решения задачи №2.

Найти производную функции.

а) б)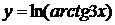

Решение: а) Данная функция является композицией двух имеющих производные функции u=sinx и f(u)=u². Применяя правило дифференцирования сложной функции, получим:

б) Аналогично здесь u=arctg3x и f(u)=ln(u). Применяя правило дифференцирования сложной функции, получим:

Ответ: а) б)

Пример решения задачи №3.

Найти производную функции, заданной параметрически.

Решение: Производная функции у(х) находится по формуле .

Ответ: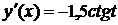

 

Пример решения задачи №5.

Найти производную функции, используя правило Лопиталя.

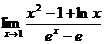
Решение: Как видно, при попытке непосредственного вычисления предела получается неопределенность вида 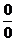. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя.

f¢(x) = 2x + ; g¢(x) = e^x;

 

Тогда получим:

;

 

Ответ:

 

Пример решения задачи №6.

Найти уравнение касательной к функции в заданной точке .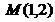

Решение:

Уравнение касательной к функции в точке определяется по формуле

Найдем производную функции

Найдем:

.

Отсюда получаем уравнение касательной:

Ответ: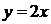

Пример решения задачи №8.

Найти производную указанного порядка.

Решение: Находим первую производную:

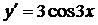
Находим вторую производную:

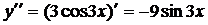
Находим третью производную:

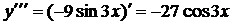
Ответ:

 

Пример решения задачи №9.

Исследовать функцию и построить ее график.

 

Решение: а) находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).

Областью значений данной функции является интервал (-¥; ¥).

б) f(x)= -f(x) - следовательно, функция нечетная.

в) функция пересекается с осями координат только в одной точке (0;0)

г) Находим интервалы знакопостоянства функции:

 

f(x)>0

Так функция нечетная то рассмотрим только в случае х>0. Получаем, что f(x)>0 при х>1 и f(x)<0 при 0<х<1.

д) Прямые х = 1, х = -1 являются вертикальными асимптотами кривой. Теперь найдем наклонные асимптоты.

 

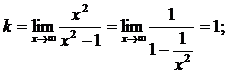
Итого, уравнение наклонной асимптоты – y = x.

е) Точками разрыва функции являются точки х = 1, х = -1.

Находим критические точки.

Найдем производную функции

 

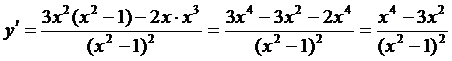
Критические точки: x = 0; x = - ; x = ; x = -1; x = 1.

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

 

-¥ < x < - , y¢ > 0, функция возрастает

- < x < -1, y¢ < 0, функция убывает

-1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < , y¢ < 0, функция убывает

< x < ¥, y¢¢ > 0, функция возрастает

 

Видно, что точка х = - является точкой максимума, а точка х = является точкой минимума. Значения функции в этих точках равны соответственно -3 /2 и 3 /2.

ж) Найдем вторую производную функции

.

 

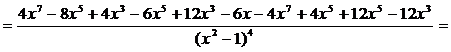
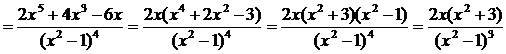Определим выпуклость и вогнутость кривой на промежутках.

-¥ < x < - , y¢¢ < 0, кривая выпуклая

- < x < -1, y¢¢ < 0, кривая выпуклая

-1 < x < 0, y¢¢ > 0, кривая вогнутая

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < , y¢¢ > 0, кривая вогнутая

< x < ¥, y¢¢ > 0, кривая вогнутая

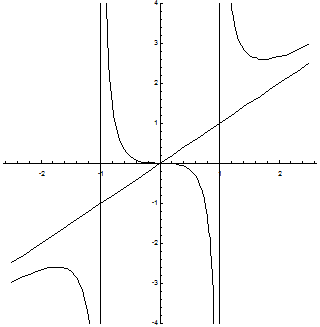
Построим график функции: