МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено
на заседании кафедры физики
08 февраля 2012 г.
Методические указания
к практическим занятиям
«Геометрическая и волновая оптика»
Методические указания для всех специальностей и
для всех профилей всех направлений бакалавриата
очной и заочной форм обучения
Ростов-на-Дону
УДК 531.383
Методические указания к практическим занятиям «Геометрическая и волновая оптика». – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 10 с.
Методические указания содержат краткую теорию по геометрической и волновой оптике, в качестве пояснений к решению серии задач данного раздела физики.
Методические указания основаны на учебном пособии «Курс физики» и на «Сборнике задач по курсу физики» Т.И. Трофимовой (изд-во Высшая школа), соответствующих действующей программе курса физики для всех специальностей и для всех профилей всех направлений бакалавриата.
Предназначены для проведения практического занятия «Геометрическая и волновая оптика» по программе курса физики для студентов всех специальностей и всех профилей всех направлений бакалавриата очной и заочной форм обучения.
УДК 531.383
Составитель доц. Е.В. Чебанова
Рецензент проф. А.Н. Павлов
Редактор Н.Е. Гладких
Темплан 2012 г., поз. ___
Подписано в печать ____). Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л 0,5. Тираж 100 экз. Заказ
Редакционно-издательский центр
Ростовского государственного строительного университета.
334022, Ростов-на-Дону, ул. Социалистическая, 162
© Ростовский государственный
строительный университет, 2012
Примеры решения задач по теме «Геометрическая и волновая оптика»
(Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.)
Задача №1 (5.7). Предельный угол полного отражения на границе стекло – жидкость i пр = 65о. Определите показатель преломления жидкости, если показатель преломления стекла n = 1,5.
 |
Дано: Решение:
Закон преломления: луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела в точке падения, лежат в одной плоскости; отношение синуса угла падения i 1 к синусу угла преломления i 2 есть величина постоянная для данных сред: 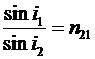 , ,
|
iпр = 65о
 n = 1,5
n = 1,5
nж –?
где n 21 – относительный показатель преломления второй среды относительно первой.
Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:
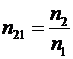 .
.
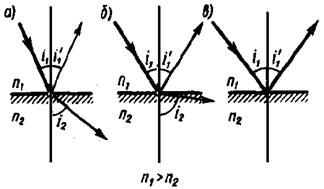
Рис. 1
Если свет распространяется из среды с большим показателем преломления n 1 (оптически более плотной) в среду с меньшим показателем преломления n 2 (оптически менее плотную) (n 1> n 2), в нашем случае из стекла (n 1= n) в жидкость (n 2= nж), то угол преломления i 2 больше,чем угол падения i 1 (рис. 1, а).С увеличением угла падения увеличивается угол преломления (рис. 1, б) до тех пор, пока при некотором угле падения (i 1= iпр) угол преломления не окажется равным 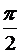 . Угол iпр называется предельным углом. При углах падения i 1 от iпр до
. Угол iпр называется предельным углом. При углах падения i 1 от iпр до 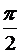 луч не преломляется, а полностью отражается в первую среду (рис. 1, в). Это явление называется полным внутренним отражением.
луч не преломляется, а полностью отражается в первую среду (рис. 1, в). Это явление называется полным внутренним отражением.
Показатель преломления жидкости nж определим из закона преломления света при подстановке в него n 1= n, n 2= nж , i 2 = 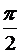 .
.
Тогда 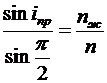 ,
,
откуда 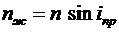 .
.
Подставим числовые значения:  .
.
Задача №2 (7.29). Двояковыпуклая линза с показателем преломления n =1,5 имеет одинаковые радиусы кривизны поверхностей, равные 10 см. Изображение предмета с помощью этой линзы оказывается в 5 раз больше предмета. Определите расстояние от предмета до изображения.
 Дано: Решение:
Дано: Решение:
 n = 1,5
n = 1,5
R1=R2=R=10 см=0,1 м

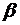 =5
=5
(a+b) –?
|
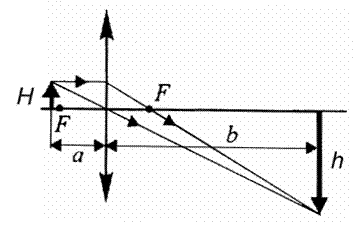
Графическое построение изображения предмета в собирающей линзе приведено на рисунке. Если предмет расположен между фокусом собирающей линзы и точкой на двойном фокусном расстоянии, то изображение предмета – действительное, обратное и увеличенное – находится с другой стороны линзы за двойным фокусным расстоянием.
Линейным увеличением линзы 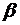 называется отношение линейных размеров изображения предмета h к линейным размерам самого предмета H, то есть:
называется отношение линейных размеров изображения предмета h к линейным размерам самого предмета H, то есть:
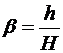 .
.
Из подобия треугольников на рисунке следует, что
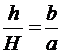 или
или 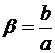 ,
,
откуда 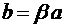 .
.
Тогда расстояние от предмета до изображения
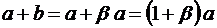 .
.
Расстояние от оптического центра линзы до предмета a определим из формулы тонкой линзы.
Формула тонкой линзы
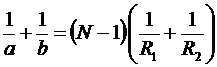 ,
,
где a и b – расстояния от оптического центра линзы соответственно до предмета и изображения;
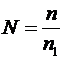 – относительный показатель преломления ( n и n1 – соответственно абсолютные показатели преломления линзы и среды, окружающей линзу );
– относительный показатель преломления ( n и n1 – соответственно абсолютные показатели преломления линзы и среды, окружающей линзу );
R1 и R2 – радиусы кривизны поверхностей линзы.
Подставив в формулу тонкой линзы:
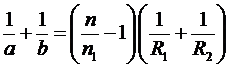
соотношения 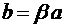 , R1=R2=R (линза имеет одинаковые радиусы кривизны поверхностей) и n1= 1 (среда, окружающая линзу, – воздух), получим:
, R1=R2=R (линза имеет одинаковые радиусы кривизны поверхностей) и n1= 1 (среда, окружающая линзу, – воздух), получим:
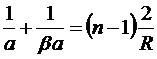
Умножим обе части выражения на 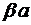 :
:
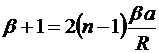 , откуда
, откуда 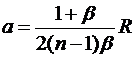 .
.
Тогда расстояние от предмета до изображения
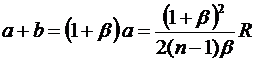 .
.
Подставим числовые значения: 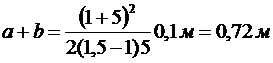 .
.
Задача №3 (5.45). Расстояние между двумя щелями в опыте Юнга d = 0,5 мм (λ = 0,6 мкм). Определите расстояние l от щелей до экрана, если ширина ∆ x интерференционных полос равна 1,2 м м.
 Дано: Решение:
Дано: Решение:
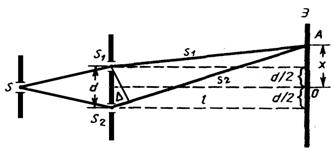 Рис. Рис.
|
d = 0,5 мм = 5 . 10–4 м
λ = 0,6 мкм = 6 . 10–7 м
 ∆ x= 1,2 мм = 1,2 . 10–3 м
∆ x= 1,2 мм = 1,2 . 10–3 м
l –?
|
В методе Юнга источником света служит ярко освещенная щель S (рис.), от которой световая волна падает на две узкие равноудаленные щели S 1 и S 2, параллельные щели S,являющиеся когерентными источниками, а интерференционная картина наблюдается на экране (Э), расположенном на некотором расстоянии l от щелей S 1 и S 2 (рис.).
Щели S 1 и S 2 находятся на расстоянии d друг от друга (рис. 4), причем l >> d.
Интерференция рассматривается в произвольной точке А на экране, расположенной на расстоянии x от точки O, симметричной относительно щелей и принятой за начало отсчета величины x.
Интенсивность в любой точке А экрана, лежащей на расстоянии х от точки О, определяется оптической разностью хода D = s 2 – s 1 .
Согласно рисунку:
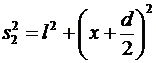 ;
; 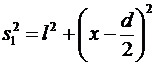 ,
,
откуда 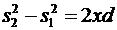
или 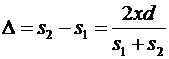 .
.
Из условия l >> d следует, что s 1 + s 2 » 2 l, тогда
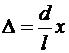 , откуда
, откуда 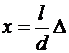 .
.
Если оптическая разность хода D равна целому числу длин волн l 0, т.е.
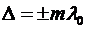 (
(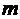 = 0, 1, 2,…),
= 0, 1, 2,…),
то колебания, возбуждаемые в точке А обеими волнами, будут происходить в
одинаковой фазе и в точке А будет наблюдаться интерференционный максимум (m – порядок интерференционного максимума).
Если же оптическая разность хода D равна полуцелому числу длин волн l 0, т.е.
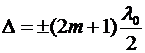 (
(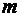 = 0, 1, 2,…),
= 0, 1, 2,…),
то колебания, возбуждаемые в точке А обеими волнами, будут происходить в противофазе и в точке А будет наблюдаться интерференционный минимум (m – порядок интерференционного минимума).
Подставляя в соотношение 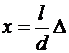 условия наблюдения интерференционных максимумов и минимумов, определим положения максимумов (xmax) и минимумов (xmin) интенсивности на экране в методе Юнга:
условия наблюдения интерференционных максимумов и минимумов, определим положения максимумов (xmax) и минимумов (xmin) интенсивности на экране в методе Юнга:
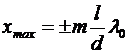 (
(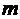 = 0, 1, 2,…),
= 0, 1, 2,…),
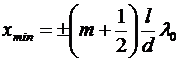 (
(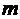 = 0, 1, 2,…).
= 0, 1, 2,…).
Расстояние между двумя соседними максимумами (или минимумами) D x называется шириной интерференционной полосы и равно:
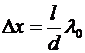 ,
,
откуда 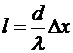 .
.
Подставим числовые значения: 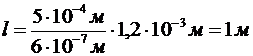 .
.
Задача №4 (5.68). Точечный источник света(λ = 0,5 мкм) расположен на расстоянии a = 1 м перед диафрагмой с круглым отверстием диаметра d = 2 мм. Определите расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.
 Дано: Решение:
Дано: Решение:
λ = 0,5 мкм = 5 . 10–7 м
a =1 м
d = 2 мм = 2 . 10–3 м
 m = 3
m = 3
b –?
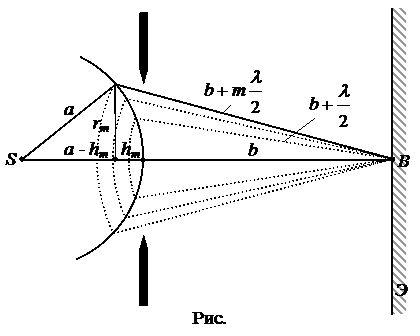
Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием (рис.). Дифракционную картину наблюдаем на экране Э в точке В, соединяющей S с центром отверстия. Согласно условию задачи, отверстие диафрагмы открывает m зон Френеля, поэтому разбиваем поверхность Ф фронта волны, идущей от источника S (поверхность Ф является сферической поверхностью с центром в точке S) на m сферических сегментов (кольцевых зон) такого размера, чтобы расстояния от краев каждой зоны до точки В отличались на l /2 (рис.). Обозначим радиус внешней границы m -ой зоны через rm, высотусферическогосегмента, выделяемого внешней границей m -ой зоны – hm.
Из рисунка 5 следует, что
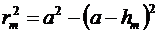 .
.
С другой стороны,
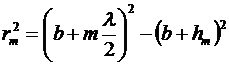 .
.
В полученных выражениях возведем скобки в квадрат:
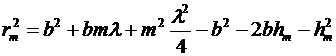 ,
,
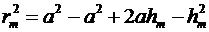 .
.
Произведем элементарные преобразования
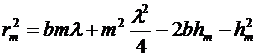 ,
,
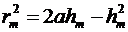 .
.
Учитывая, что 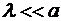 и
и 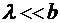 , слагаемым
, слагаемым 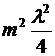 можно пренебречь по сравнению
можно пренебречь по сравнению 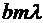 . При не слишком больших m (по условию задачи m = 3) высота сегмента
. При не слишком больших m (по условию задачи m = 3) высота сегмента 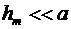 и
и 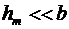 , поэтому слагаемым
, поэтому слагаемым 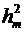 можно пренебречь по сравнению
можно пренебречь по сравнению 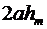 и
и 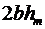 .
.
C учетом этих приближений:
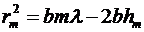 ,
,
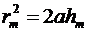 .
.
Отсюда
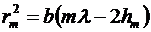 ,
,
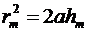 .
.
или
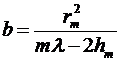 ,
,
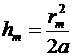 .
.
После подстановки 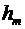 в формулу, определяющую расстояние b от диафрагмы до точки наблюдения, получим
в формулу, определяющую расстояние b от диафрагмы до точки наблюдения, получим
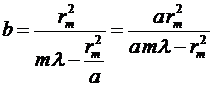 .
.
Учитывая, что 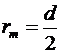 , найдем
, найдем 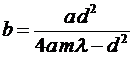 .
.
Подставим числовые значения: 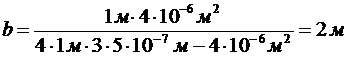 .
.
Задача №5 (5.88). На дифракционную решетку нормально падает монохроматический свет с длиной волны λ = 600 нм. Определите наибольший порядок спектра, полученный с помощью этой решетки, если ее постоянная d = 2 мкм.
 Дано: Решение:
Дано: Решение:
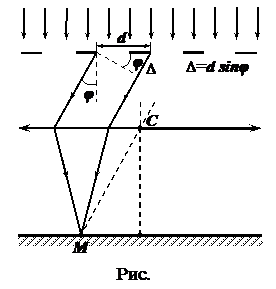 λ = 600 нм = 6 . 10–7 м
λ = 600 нм = 6 . 10–7 м
d = 2 мкм = 2 . 10–6 м 
mmax –?
Формула дифракционной решетки: (условие наблюдения максимумов(рис.)):
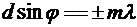 (
(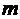 = 0, 1, 2, …, mmax),
= 0, 1, 2, …, mmax),
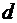 – постоянная дифракционной решетки;
– постоянная дифракционной решетки;
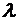 – длина световой волны;
– длина световой волны;
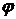 – угол дифракции,
– угол дифракции,
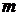 – номер дифракционных максимумов (порядок спектра),
– номер дифракционных максимумов (порядок спектра),
mmax – наибольший номер дифракционных максимумов (наибольший порядок спектра).
Наибольший порядок спектра mmax найдем, записав формулу дифракционной решетки в виде:
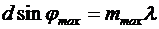 , откуда
, откуда 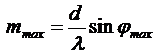 .
.
Поскольку наибольший угол дифракции не может быть более 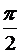 (
(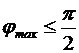 ), то
), то 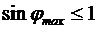 и
и 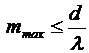 .
.
Оценим отношение 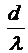 :
: 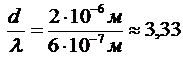 .
.
Учитывая, что число m (порядок спектра) должно быть целым, то наибольший порядок спектра mmax,полученный с помощью данной решетки: mmax = 3.
 2017-12-14
2017-12-14 612
612






