Итак – сгруппировали выборку и записали ряды частот – построили статистический ряд распределения

БАЛТИЙСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ РЫБОПРОМЫСЛОВОГО ФЛОТА

Транспортный факультет

Кафедра: «Эксплуатация транспортно-технологических машин и комплексов»

КУРСОВАЯ РАБОТА

 

По дисциплине «Спец. главы математики»

Тема: «Методы анализа экспериментальных данных и методы классического регрессивного анализа в инженерном эксперименте»

(БГАРФ. 23.03.03 – ЭТМбз-2.)

Выполнил: Специальность: Курс: Шифр: Проверил

Шустов М.В. Эксплуатация транспортно-технологических машин и комплексов Корнева И.П.

Калининград

Задача 1. По данным выборки:

1) построить статистический ряд распределения;

2) изобразить гистограмму;

3 ) вычислить выборочное среднее;

4) вычислить выборочную дисперсию.

Решение:

1. Выборка размером 100 чисел. Для начала найдем минимальное и максимальное числа в этой выборке. Минимум – 0,2, максимум – 5,4. Тогда размах выборки R = 5,4-0,2 = 5,2. Определим число интервалов, на которые будем разбивать выборку: Длина одного интервала определяется по формуле h = R/k = 5,2/8 = 0,65.

Зная на сколько интервалов (8) какой длины (0,65) нужно разбивать выборку, сделаем это.

Номер инт	Интервал	Частоты	Середины	Относит. Частоты
	0,2-0,85		0,525	0,03
	0,85-1,5		1,175	0,03
	1,5-2,15		1,825	0,12
	2,15-2,8		2,475	0,25
	2,8-3,45		3,125	0,29
	3,45-4,1		3,775	0,16
	4,1-4,75		4,425	0,08
	4,75-5,4		5,075	0,04
Всего

Итак – сгруппировали выборку и записали ряды частот – построили статистический ряд распределения.

Гистограмма – это график, представленный в виде диаграммы со столбцами вместо точек, высоты которых равны cответствующим частотам:

 

1. Далее найдем некоторые числовые характеристики.

Номер инт	Интервал	Частоты	Середины	Относит. Частоты	mi*xi	mi*(xi-xср)^2
	0,2-0,85		0,525	0,03	1,575	17,729
	0,85-1,5		1,175	0,03	3,525	4,142
	1,5-2,15		1,825	0,12	21,9	39,968
	2,15-2,8		2,475	0,25	61,875	153,141
	2,8-3,45		3,125	0,29	90,625	283,203
	3,45-4,1		3,775	0,16	60,4	228,010
	4,1-4,75		4,425	0,08	35,4	156,645
	4,75-5,4		5,075	0,04	20,3	1041,420
Всего					2,956	19,243

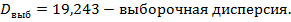
Задача 2. Используя метод наименьших квадратов, найти параметры зависимости

1) в предположении, что эта зависимость линейна;

2) в предположении, что зависимость нелинейная, выбрав по форме данных ее наиболее вероятный вид;

а) указать а и в для линейной зависимости;

б) форму нелинейной зависимости;

в) а и в для нелинейной зависимости;

г) величины средних квадартических отклонений для линейного и нелинейного случаев.

Решение:

Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a
Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Для оценки параметров α и β - используют МНК (метод наименьших квадратов).
Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии. Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).
Формально критерий МНК можно записать так:
S = ∑(y_i - y^*_i)² → min
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

x	y	x2	y2	x • y
	16.9		285.61	33.8
	19.5		380.25	58.5
	24.5		600.25
	35.2		1239.04	211.2
	41.3		1705.69	289.1
	48.2		2323.24	385.6
	64.6		4173.16
	72.3		5227.29	795.3
	410.5		20144.53	3185.5

 

 

Для наших данных система уравнений имеет вид
10a + 65 b = 410.5
65 a + 505 b = 3185.5
Домножим уравнение (1) системы на (-6.5), получим систему, которую решим методом алгебраического сложения.
-65a -422.5 b = -2668.25
65 a + 505 b = 3185.5
Получаем:
82.5 b = 517.25
Откуда b = 6.2697
Теперь найдем коэффициент «a» из уравнения (1):
10a + 65 b = 410.5
10a + 65 • 6.2697 = 410.5
10a = 2.97
a = 0.297
Получаем эмпирические коэффициенты регрессии: b = 6.2697, a = 0.297
Уравнение регрессии (эмпирическое уравнение регрессии):
y = 6.2697 x + 0.297
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
1. Параметры уравнения регрессии.
Выборочные средние.
x ср – 6,5;

У ср – 41,05;
Среднеквадратическое отклонение

S(x) – 2.872;

S(y) – 18.148.
Нелинейная зависимость:

СистемауравненийМНК:
a₀n + a₁∑x + a₂∑x² = ∑y
a₀∑x + a₁∑x² + a₂∑x³ = ∑yx
a₀∑x² + a₁∑x³ + a₂∑x⁴ = ∑yx²

x	y	x2	y2	x y	x3	x4	x2 y
	16.9		285.61	33.8			67.6
	19.5		380.25	58.5			175.5
	24.5		600.25
	35.2		1239.04	211.2			1267.2
	41.3		1705.69	289.1			2023.7
	48.2		2323.24	385.6			3084.8
	64.6		4173.16
	72.3		5227.29	795.3			8748.3
	410.5		20144.53	3185.5			27611.1

Для наших данных система уравнений имеет вид
10a₀ + 65a₁ + 505a₂ = 410.5
65a₀ + 505a₁ + 4355a₂ = 3185.5
505a₀ + 4355a₁ + 39973a₂ = 27611.1
Получаем a₂ = 0.297, a₁ = 2.414, a₀ = 10.381
Уравнение регрессии:
y = 0.297x²+2.414x+10.381.

Задача 3. По данным выборки, удовлетворяющей нормальному закону распределения, вычислить:

1) выборочное среднее;

2) исправленное выборочное среднее квадратическое отклонение;

3) доверительный интервал для математического ожидания для доверительной вероятности гамма;

4) доверительный интервал для среднего квадратического отклонения для того же значения гамма.

Решение:

18,3
15,5
24,5
24,7
13,3
15,4
10,1
23,1
19,3
5,7
11,6
14,3
4,5
20,3
32,3

Дисперсия D = σ² = 4.6² = 21.16
Доверительный интервал для генерального среднего.

Поскольку n ≤ 30, то определяем значение t_kp по таблице распределения Стьюдента
По таблице Стьюдента находим:
T_табл (n-1;α/2) = (16;0.025) = 2.131

С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала (14,45;19,35).

Доверительный интервал для среднеквадратического отклонения.
S(1-q) < σ < S(1+q)
Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.95 и объему выборки n = 16
По таблице q=q(γ; n) определяем параметр q(0.95;16) = 0.37
4.6(1-0.37) < σ < 4.6(1+0.37)
2.898 < σ < 6.302
Таким образом, интервал (2.898;6.302) покрывает параметр σ с надежностью γ = 0.95

 

Задача 4. По данным выборки, удовлетворяющей нормальному закону распределения со средним квадратическим отклонением, вычислить:

1) выборочное среднее;

2) доверительный интервал для математического ожидания для доверительной вероятности гамма.

Решение:

38,3	27,8	26,3	19,6
26,1	23,8		40,8
10,5	19,8	37,3	18,4
26,9	24,7	25,1	30,1
25,4	29,2	17,4	26,1
12,1	24,4	37,1
12,3	5,6	29,6	40,3
15,1	19,4	27,9	27,4
	30,1	30,1	20,1
21,6	15,3	6,2	29,2
23,5	8,4	20,8
	14,2		31,5
21,4	22,8	19,2	34,7
24,1	30,8	20,9	5,1
26,6	36,2		24,6
25,8		22,2	8,1
12,7	20,5	12,7	33,7
15,2	14,1	15,5	32,2
32,9	18,6	19,6	10,3
22,1	14,7	24,5
25,7	24,1	24,2	12,6
13,6	26,9	35,4
27,8	26,2	34,7	28,4
22,8	8,8	25,1	11,1
10,1	22,5	14,1	33,4

Доверительный интервал для генерального среднего.

Поскольку n>30, то определяем значение t_kp по таблицам функции Лапласа.
В этом случае 2Ф(t_kp) = γ
Ф(t_kp) = γ/2 = 0.99/2 = 0.495
По таблице функции Лапласа найдем, при каком t_kp значение Ф(t_kp) = 0.495
t_kp(γ) = (0.495) = 2.58

(20.78;25.42)
С вероятностью 0.99 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.

Задача 5. По данным выборки двумерной случайной величины определить:

1) вектор математического ожидания;

2) вектор дисперсии;

3) выборочный коэффициент корреляции;

4) выборочное уравнение прямой оинии регрессии у на х.

Решение:

x	y
41,2	116,5
48,1	124,6
53,2	153,9
39,1
50,2	191,6
	94,9
39,4	100,2
50,2	178,6
48,3	118,7
39,6
41,3	81,7
35,2
47,9	159,4
34,6	124,4
33,2	103,4
35,7	94,9
36,8	90,8
50,8	180,5
44,5
46,3	167,6
34,8	84,6
39,2	124,5
36,8	131,7
	99,8
40,4	144,8
41,5	120,6
44,5	109,7
38,9	93,5
49,8	136,8
45,6	107,6
	102,9
47,6	102,9
32,5	116,7
54,1	157,9
35,4	109,1
37,9	92,4
38,6	120,7
35,6	96,1
33,6	73,2
27,7	61,5
47,1
29,9	82,8
50,1	110,5

Составим вспомогательную таблицу:

x	y	x^2	y^2	x*y
41,2	116,5	1697,44	13572,25	4799,8
48,1	124,6	2313,61	15525,16	5993,26
53,2	153,9	2830,24	23685,21	8187,48
39,1		1528,81		3870,9
50,2	191,6	2520,04	36710,56	9618,32
	94,9		9006,01	3701,1
39,4	100,2	1552,36	10040,04	3947,88
50,2	178,6	2520,04	31897,96	8965,72
48,3	118,7	2332,89	14089,69	5733,21
39,6		1568,16		4633,2
41,3	81,7	1705,69	6674,89	3374,21
35,2		1239,04		3097,6
47,9	159,4	2294,41	25408,36	7635,26
34,6	124,4	1197,16	15475,36	4304,24
33,2	103,4	1102,24	10691,56	3432,88
35,7	94,9	1274,49	9006,01	3387,93
36,8	90,8	1354,24	8244,64	3341,44
50,8	180,5	2580,64	32580,25	9169,4
44,5		1980,25
46,3	167,6	2143,69	28089,76	7759,88
34,8	84,6	1211,04	7157,16	2944,08
39,2	124,5	1536,64	15500,25	4880,4
36,8	131,7	1354,24	17344,89	4846,56
	99,8		9960,04	4590,8
40,4	144,8	1632,16	20967,04	5849,92
41,5	120,6	1722,25	14544,36	5004,9
44,5	109,7	1980,25	12034,09	4881,65
38,9	93,5	1513,21	8742,25	3637,15
49,8	136,8	2480,04	18714,24	6812,64
45,6	107,6	2079,36	11577,76	4906,56
	102,9		10588,41	3395,7
47,6	102,9	2265,76	10588,41	4898,04
32,5	116,7	1056,25	13618,89	3792,75
54,1	157,9	2926,81	24932,41	8542,39
35,4	109,1	1253,16	11902,81	3862,14
37,9	92,4	1436,41	8537,76	3501,96
38,6	120,7	1489,96	14568,49	4659,02
35,6	96,1	1267,36	9235,21	3421,16
33,6	73,2	1128,96	5358,24	2459,52
27,7	61,5	767,29	3782,25	1703,55
47,1		2218,41		4474,5
29,9	82,8	894,01	6855,84	2475,72
50,1	110,5	2510,01	12210,25	5536,05
41,3	116,98	1748,841	14562,22	4964,156

 

 

 

 

Уравнение регрессии:

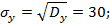
Задача 6. По данным 2 выборок вычислить коэффициенты ранговой корреляции Спирмена и Кендалла.

Решение:

Присвоим ранги признаку Y и фактору X.

X	Y	ранг X, dx	ранг Y, dy

Матрица рангов.

ранг X, dx	ранг Y, dy	(dx - dy)2

Проверка правильности составления матрицы на основе исчисления контрольной суммы:
Сумма по столбцам матрицы равны между собой и контрольной суммы, значит, матрица составлена правильно.
По формуле вычислим коэффициент ранговой корреляции Спирмена.
Связь между признаком Y и фактором X умеренная и обратная

Коэффициент Кендэла.

Упорядочим данные по X.
В ряду Y справа от 1 расположено 17 рангов, превосходящих 1, следовательно, 1 породит в Р слагаемое 17.
Справа от 2 стоят 16 ранга, превосходящих 2 (это 14, 12, 10, 11, 7, 18, 15, 17, 16, 13, 8, 5, 9, 6, 3, 4), т.е. в Р войдет 16 и т.д. В итоге Р = 66 и с использованием формул имеем:

X	Y	ранг X, dx	ранг Y, dy	P	Q

 

По упрощенным формулам: