2018-01-08
545
ОПРЕДЕЛЕНИЕ ЭКВИПОТЕНЦИАЛЬНЫХ ПОВЕРХНОСТЕЙ
И ЛИНИЙ НАПРЯЖЕННОСТИ ЭЛЕКТРОСТАТИЧЕСКОГО
ПОЛЯ
Цель работы: исследование электрических полей, создаваемых несколькими зарядами.
Оборудование: установка для исследования электростатических полей, источник питания 0¸7В, токопроводящая бумага, поверх которой прикреплена декоративная панель с многочисленными отверстиями, мультиметр в режиме вольтметра.
Краткая теория
Система тел или частиц называется электрически изолированной системой, если между ней и внешними телами нет обмена электрическими зарядами.
Закон сохранения электрического заряда: алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе
.
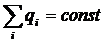Удаленные друг от друга точечные электрические заряды взаимодействуют по закону Кулона с силой:
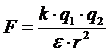, (1.1)
где k = 9 × 109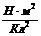 
- коэффициент пропорциональности, который можно определить по формуле 
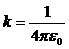, e0 - электрическая постоянная, равная 8,85 × 10-12 
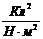, q1 и q2 - точечные заряды, находящиеся на расстоянии r друг от друга.
|
|
|
Точечным зарядом q называется наэлектризованное тело, размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми оно взаимодействует, e - диэлектрическая проницаемость среды, равная отношению силы взаимодействия между зарядами в отсутствии среды F0 и при ее наличии F.
 .
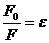| (1.2) |
Каким же образом осуществляется это взаимодействие при отсутствии вещества между зарядами? Взаимодействие между зарядами происходит через посредство электрического поля. Электрическое поле, образованное системой неподвижных зарядов называется электростатическим.
Если рассмотреть заряд q как «источник» электрического поля, в которое на расстоянии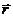 
помещен пробный заряд 
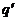, то на него будет действовать сила:
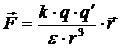, (1.3)
где 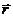- радиус вектор, проведенный от заряда 
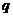к заряду .
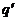Отсюда видно, что сила зависит от величины пробного заряда q’: F~ q’. С другой стороны,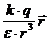 
не зависит от q’, а зависит от величины заряда q, свойств среды e и положения в пространстве той точки, в которой изучается поле - значения радиус-вектора 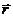. Эту величину можно принять для количественной характеристики электрического поля:
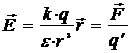. (1.4)
Вектор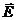 
носит название вектора напряженности электрического поля и служит его силовой характеристикой. В СИ 
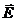измеряется в В/м.
Вектор напряженности электрического поля системы зарядов равен геометрической сумме напряженности полей, создаваемых в данной точке каждым из зарядов в отдельности.
|
|
|
.
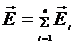Это утверждение называется принципом суперпозиции (наложения) электрических полей.
Графически электрическое поле можно показать с помощью силовых линий. Эти линии проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором 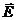в той же самой точке (рис.1.1).
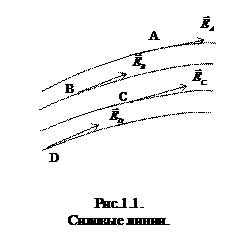Условно принимают, что число линий, проходящих через единичную площадку, ориентированную перпендикулярно этим линиям, должно равняться численной величине Е в данной области поля. Свойство линий напряженности начинаться или заканчиваться только на электрических зарядах или уходить в бесконечность, сохраняется и для полей, создаваемых любой системой электрических зарядов. В качестве примера использования принципа суперпозиции электрических полей рассмотрим поле электрического диполя. Диполем называется совокупность двух одинаковых по абсолютной величине разноименных зарядов + q и - q, расположенных на расстоянии l друг от друга, которое мало по сравнению с расстоянием r от центра диполя О до точки М, в которой определяется напряженность 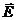(рис.1.2.).
Соединим точку наблюдения М с обоими зарядами радиус-векторам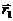и 
и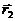 
, проведенными из тех точек, в которых находятся эти заряды. Тогда, вектор напряженности 
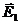создаваемый зарядом - q в точке М, будет направлен против радиус-вектор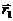а , а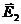 
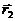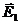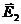будет направлен по . Векторы и определяются по формуле (1.4), а полный вектор напряженности электрического поля в точке М равен их геометрической сумме:
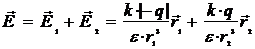. (1.5)
|
Из треугольника ОLM на рисунке видно, что вектор 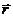является геометрической суммой вектора 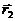и вектора 
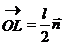, где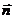 
- единичный вектор, направленный вдоль прямой, соединяющей заряды 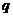и - 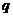. Отсюда 
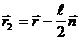и аналогично 
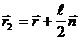. (1.6) Опуская из точки L перпендикуляр на радиус вектор 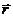, мы видим, что величина
r = ON 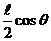+ NM = 
+ NM.
Используя условие l << r, мы можем считать в прямоугольном треугольнике LNM катет NM равным гипотенузе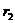 
; тогда
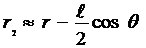и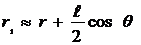 
. (1.7)
Подставляя (1.7) в (1.5), получаем:
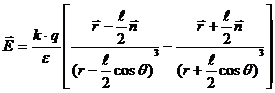. (1.8)
Раскрывая скобки в знаменателях по формуле бинома Ньютона и отбрасывая члены, содержащие малые порядки l2 и l3, имеем:
.
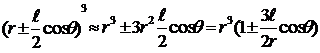Воспользуемся правилом приближенного деления, согласно которому при относительной ошибке d <<1 c точностью до членов второго порядка
.
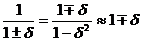Тогда
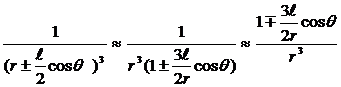. (1.9)
Подставляя (1.9) в (1.8) и раскрывая скобки, получим:
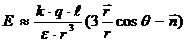. (1.10)
Отсюда видно, что напряженность поля диполя определяется не в отдельности величиной зарядов q и расстоянием между ними l, а произведением
p = ql, (1.11)
которое называется дипольным моментом. Поскольку ось диполя ориентирована в пространстве, то дипольный момент является вектором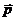 
. Он направлен вдоль оси диполя от отрицательного заряда к положительному, т.е. по единичному вектору 
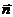. Следовательно,
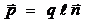. (1.12)
Подставляя (1.11) и (1.12) в (1.10), получаем
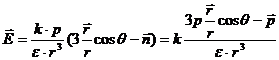. (1.13)
Значит, напряженность электрического поля диполя Е прямо пропорциональна величине дипольного момента p и в любом направлении (для любых q) убывает с ростом r как 1/r3.
Теорема Остроградского-Гаусса
Потоком вектора напряженности электрического поля сквозь малый участок поверхности, проведенной в поле, называется величина
dN = E dS cos (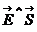
)= 
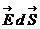. (1.17)
где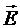 
- вектор напряженности электрического поля в точках малого участка поверхности площадью dS, 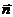- единичный вектор, нормальный к площадке dS, а вектор 
.
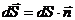dN = EndS = EdS^. (1.18)
Поток напряженности N сквозь любую поверхность S равен алгебраической сумме потоков напряженности сквозь все малые участки этой поверхности:
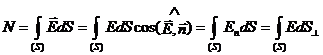. (1.19)
При этом все векторы 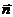нормалей к малым площадкам dS нужно направлять в одну и ту же сторону относительно поверхности S.
Рассмотрим электростатическое поле системы точечных зарядов q1, q2,..., qn. Согласно принципу суперпозиции полей:
|
|
|
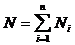, (1.20)
т.е. искомый поток N равен алгебраической сумме потоков через ту же замкнутую поверхность S напряженности полей каждого из зарядов системы. Поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической сумме электрических зарядов, охватываемых этой поверхностью, к электрической постоянной e0.
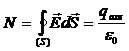. (1.21)
Рассмотрим несколько примеров использования теоремы Остроградского-Гаусса.
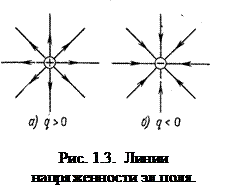Точечный заряд
Рассмотрим точечный заряд, помещенный в центре сферы радиусом R. По теореме Остроградского-Гаусса dN = EdS =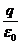 
, учитывая, что Sсферы = 4pR2, то
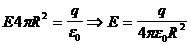. (1.22)
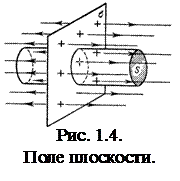Бесконечно заряженная плоскость
Рассмотрим равномерно заряженную бесконечную плоскость с постоянной поверхностной плотностью заряда s:
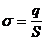- это заряд, распределенный по площади S.
Вектор электрического поля будет направлен нормально от плоскости, если s>0.
Для определения модуля вектора напряженности, создаваемого пластиной, применим теорему Гаусса к замкнутой цилиндрической поверхности (рис. 1.4). Ось цилиндра перпендикулярна заряженной плоскости, и последняя делит высоту цилиндра пополам. Оба основания параллельны заряженной плоскости и имеют одинаковую площадь S.
Поток вектора напряженности через цилиндрическую поверхность равен:
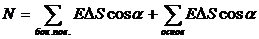(1.23)
На боковой поверхности вектор E параллелен поверхности и cosα = 0. На торцах цилиндра вектор E перпендикулярен поверхности и cosα = 1, а величина E одинакова на обоих основаниях; следовательно,
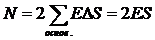(1.24)
Проведенная цилиндрическая поверхность вырезает из плоскости такую же площадку S c полным зарядом:
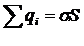(1.25)
Подставляя (1.24) и (1.25) в левую и правую части (1.21) получаем:
откуда
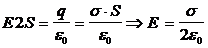(1.26)
