Проверка распределением хи-квадрат

Вариант № 10

Ситуационная (практическая) задача № 1

Время ξ (в мин.) между прибытием двух автомашин к светофору является случайным с плотностью распределения

§ Установить неизвестную постоянную С и построить график функции p(x).

§ Найти функцию распределения с.в. ξ и построить её график.

§ Вычислить математическое ожидание (среднее значение) Мξ, дисперсию Dξ и среднее квадратическое (стандартное) отклонение рассматриваемой случайной величины

§ Во сколько раз число прибывших к светофору автомашин со временами между прибытиями больше среднего превосходит число автомашин со временами между прибытиями меньше среднего?

§

Ситуационная (практическая) задача № 2

При измерении веса 25 упаковок сильнодействующего лекарственного

препарата были обнаружены следующие отклонения (в гр.) от указанного на

обертке:

–24.34, –14.59, –18.27, –8.94, –15.09, –10.94, 4.47, 3.05, –8.33, –22.98, 1.75,

–32.07, –7.43, –18.63, –12.97, –11.08, –7.44, –1.70, 6.34, –11.08, –11.12,

–15.90, –10.26, –8.07, –6.48

. Необходимо:

§ Определить исследуемый признак и его тип (дискретный или непрерывный).

Строим «полигон» (см. график «полигон» по упорядоченным значениям, и аппроксимируем линейной функцией (там же). Видим, что коэффициент корреляции Пирсона (R) = 0.956 (корень из R²), P<0.001, т.е. корреляция высоко достоверна, данные расположены равномерно, без дискретных скачков, следовательно, признак непрерывный.

§ В зависимости от типа признака построить полигон или гистограмму относительных частот.

Разбиваем интервал значений данных [-32.07, 6.34] на 5 интервалов [-oo,-30; -30-20; -20-10; -10-0; 0-10], и подсчитываем число точек в каждом. Получаем «гистограмму наблюдений».

§ На основе визуального анализа полигона (гистограммы) сформулировать гипотезу о законе распределения признака.

Так как данные распределены равномерно, справедлив нормальный закон распределения. Это же подтверждается гистограммой наблюдений («гистограмма»). Функция нормального распределения со средним -10.5 и стандартным отклонением 9.05 для интервала измерений -30..10 приведена в таблице1 «Нормальное распределение по интервалам».

§ Вычислить выборочные характеристики изучаемого признака: среднее, дисперсию, среднее квадратическое (стандартное) отклонение.

Используя стандартные функции (внизу упорядоченного ряда данных в основном листе файла) получаем среднее, дисперсию, стандартное отклонение. Формулы есть в любом учебнике – если надо – запросите меня.

§ Используя критерий согласия «хи-квадрат» Пирсона, проверить соответствие выборочных данных выдвинутому в п.3 закону распределения при уровне значимости 0,05.

На основании таблицы наблюдаемых и ожидаемых численностей считаем критерий хи-квадрат

, получаем значение chi-2 =1.99 df =4 (5 интервалов -1), P =0.77 (см файл эксел). Таким образом, P >0.05 и наблюдаемое распределение не отличается достоверно от нормального.

§ Для генеральной средней и дисперсии построить доверительные интервалы, соответствующие доверительной вероятности 0,95.

§ С надежностью 0,95 проверить гипотезу о равенстве:

а) генеральной средней значению -10;

б) генеральной дисперсии значению 100.

 

10. Для сигнализации об аварии в офисе некоторой фирмы города N установлено три сигнализатора различных типов, которые работают независимо друг от друга. Во время аварии сигнализаторы первого типа не срабатывают в среднем в 10%, второго – 8%, третьего 15% всех аварийных случаев. Рассматривается случайная величина x - число сработавших сигнализаторов во время аварии. Найти .

А. 0,2962

Б. 0,7038

В. 0,2636

Г. 0,0314

 

Проверка распределением хи-квадрат

Если выборка достаточно велика, применяются иные критерии согласия, наиболее надежным и универсальным из которых является критерий Пирсона 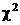. Применяя данный критерий необходимо выполнить следующие действия.

Область возможных значений случайной величины разбивается на конечное число () непересекающихся интервалов:

Для каждого интервала 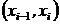подсчитывается число элементов выборки, попавших в данный интервал.

Вычисляется теоретическая вероятность попадания в -й интервал при нормальном законе распределения вероятностей

,

где 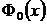- функция Лапласа.

Проверяется выполнение условия для всех интервалов; интервалы, для которых это условие не выполнено, объединяются с соседними интервалами.

Вычисляется сумма

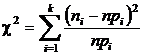, (5)

имеющая приближенно - распределение с степенями свободы.

При заданной доверительной вероятности 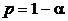( - уровень значимости) и числе степеней свободы вычисляется (или находится по таблицам) критическое значение критерия .

Если

, (6)

то гипотеза принимается, т. е. можно считать, что распределение вероятностей рассматриваемой серии измерений не отличается от нормального.

Необходимо помнить о вероятностном характере выводов, поэтому никакая, даже самая малая величина суммы (5) не может служить доказательством нормальности закона распределения.