Цей метод використовується для знаходження розв’язку лінійної системи рівнянь А х = b, (2) в якій матриця А = (а  ) симетрична, тобто елементи, симетричні відносно головної діагоналі, рівні між собою: а
) симетрична, тобто елементи, симетричні відносно головної діагоналі, рівні між собою: а  = а
= а  (i, j = 1,2, …, n). Відомо, що симетричну матрицю А завжди можна подати у вигляді добутку двох взаємно транспонованих трикутних матриць А = Т΄Т, (3)
(i, j = 1,2, …, n). Відомо, що симетричну матрицю А завжди можна подати у вигляді добутку двох взаємно транспонованих трикутних матриць А = Т΄Т, (3)
де Т =  ; Т΄ =
; Т΄ =  .
.
Якщо тепер перемножити матриці Т΄ і Т, а потім прирівняти відповідні елементи матриць у рівності (3), то для знаходження 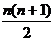 елементів t
елементів t 
(i = 1, 2, …, n; j = i, i +1, …, n) матриці Т дістанемо систему 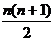 рівнянь
рівнянь
 (i = 1, 2, …, n; j = i +1, i +2, …, n; i
(i = 1, 2, …, n; j = i +1, i +2, …, n; i  j).
j).
З цієї системи знаходимо послідовно елементи матриці Т (і Т΄).
Маємо  (4)
(4)
З рівності (3) випливає, що система (2) рівносильна двом системам рівнянь з трикутними матрицями Т΄ y = b і Т x = y.
Розв’язавши систему Т΄ y = b з нижньою трикутною матрицею Т΄, знайдемо  (5)
(5)
Розв’язавши потім систему Т x = y з верхньою трикутною матрицею Т, знайдемо шуканий розв’язок системи (2) 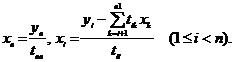 (6)
(6)
Всі обчислення за формулами (4)–(6) доцільно виконувати за спеціальною схемою (табл. 1), в якій забезпечується проміжний і заключний контролі введенням контрольних і рядкових сум. У методі квадратних коренів, як і в методі Гауса, поряд з системою (2) одночасно розв’язують допоміжну систему А  =s. (7)
=s. (7)
Таблиця 1
| Крок пере-тровення | Рядок | Коефіцієнти при змінних | Вільний член | Контроль | ||||
x 
| x 
| … | x 
| Контрольна сума | Рядкова сума | |||
| … | n+2 | n+3 | n+4 | n+5 | ||||
a 
| a 
| a 
| b 
| s 
| ||||
a 
| a 
| b 
| s 
| |||||
| … | … | … | … | … | … | … | ||
| n | a 
| b 
| s 
| |||||
| n+1 | t 
| t 
| … | t 
| y 
| z 
| u 
| |
| n+2 | t 
| … | t 
| t 
| z 
| u 
| ||
| … | … | … | … | … | … | |||
| 2n | t 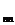
| y 
| z 
| u 
| ||||
| 2n+1 | x 
|  
| 1+ x 
| |||||
| … | … | … | … | … | … | |||
| 3n-1 | x 
|  
| 1+ x 
| |||||
| 3n | x 
|  
| 1+ x 
|
Системи (2) і (7) мають однакову матрицю коефіцієнтів А, але різні вільні члени: у системі (2) – це числа b  (i = 1, 2, …, n), а в системы (7) – числа
(i = 1, 2, …, n), а в системы (7) – числа
s  =
= 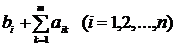 (8)
(8)
Розв’язки цих систем зв’язані співвідношенням:
 (9)
(9)
Оскільки система (7) рівносильна двом системам з трикутними матрицями Т´ z = s i T  = z, то елементи вектора z обчислюють за формулами
= z, то елементи вектора z обчислюють за формулами
z 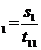 , z
, z  , (1 < i
, (1 < i  n), (10)
n), (10)
а елементи вектора  – за формулами
– за формулами

 ,
, 
 , (1 < i
, (1 < i  n). (11)
n). (11)
Поточний контроль здійснюють порівнянням контрольних сум z  (стовпець n+4), які обчислюють за формулами
(стовпець n+4), які обчислюють за формулами
u 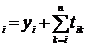 (і = 1,2,3 …, n). (12)
(і = 1,2,3 …, n). (12)
Якщо обчислення виконано правильно, то суми збігаються, або внаслідок округлення проміжних обчислень відрізняться між собою на 1-2 одиниці нижчого розряду. Всі проміжні обчислення доцільно виконувати з 1-2 запасними цифрами.
Заключний контроль можна здійснити двояко. Або перевірити виконання рівностей (9) або (і) обчислити нев’язки, підставивши знайдений розв’язок у систему (2).
Розрахункова таблиця 1 складається з трьох частин. У першій записано коефіцієнти і вільні члени системи(2), а також обчислені за формулами (8) контрольні суми s  (рядкові суми можна не записувати, бо вони збігаються з контрольними); у другій знайдені за формулами(4) коефіцієнти t
(рядкові суми можна не записувати, бо вони збігаються з контрольними); у другій знайдені за формулами(4) коефіцієнти t  (i =1, 2, …, n; j = i +1, і +2, …, n) матриці Т, обчислені за формулами (5) і (10) вектори y i z, а також обчислені за формулами (12) рядкові суми u
(i =1, 2, …, n; j = i +1, і +2, …, n) матриці Т, обчислені за формулами (5) і (10) вектори y i z, а також обчислені за формулами (12) рядкові суми u  (i = 1, 2, …, n); у третій – обчислені за формулами (6) і (11) вектори x і
(i = 1, 2, …, n); у третій – обчислені за формулами (6) і (11) вектори x і  . Дві перші частини – це прямий хід, а третя – зворотній.
. Дві перші частини – це прямий хід, а третя – зворотній.
Завдання
Розв’язати систему лінійних рівнянь методом квадратних коренів з точністю до 0,001.
№1 
№2 
№3 
№4 
№5 
№6 
№7 
№8 
№9 
№10 
№11 
№12 
№13 
№14 
№15 
№16 
№17 
№18 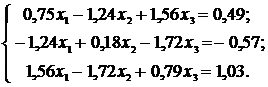
№19 
№20 
№21 
№22 
№23 
№24 
№25 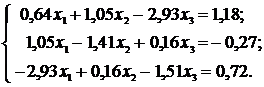
№26 
№27 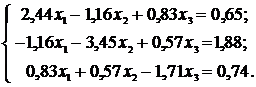
№28 
№29 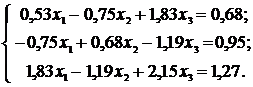
№30 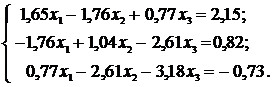
№31

№32

№33

№34

№35

№36

 2018-01-08
2018-01-08 578
578







