Линейные, разветвляющиеся и циклические алгоритмы
Цель работы: составление линейных, разветвляющихся и простых циклических алгоритмов. При подготовке к работе изучить теоретический материал (с. 4 — 8).
Задание №1. Для каждого варианта задан технологический аппарат, состоящий из трех фигур вращения (табл. Л1.1). Формулы объемов каждой из фигур приведены в табл. Л1.1а. Выполнить математическую формулировку задачи и составить линейный алгоритм вычисления полного объема технологического аппарата.
Таблица Л1.1 — Варианты заданий
| Перечень технологических аппаратов | ||||
  1 1
|  2 2
|  3 3
|  4 4
| |
 6 6
|  7 7
|  8 8
|  9 9
|  10 10
|
 11 11
|  12 12
|  13 13
|  14 14
|  15 15
|
 16 16
|  17 17
|  18 18
|  19 19
|  20 20
|
 21 21
|  22 22
|  23 23
|  24 24
|  25 25
|
 26 26
|  27 27
|  28 28
|  29 29
|  30 30
|
Таблица Л1.1а — Формулы объемов фигур
 r Конус
h
Объем равен v=p×r2×h/3 r Конус
h
Объем равен v=p×r2×h/3
| 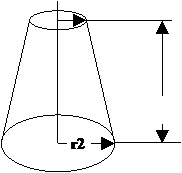 r1 Усеченный конус
h
Объем равен
v= p×h×(r12+r22+r1×r2)/3 r1 Усеченный конус
h
Объем равен
v= p×h×(r12+r22+r1×r2)/3
| ||||||
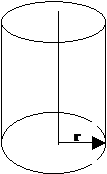 Цилиндр Цилиндр
h
v = p×r2×h | Полусфера
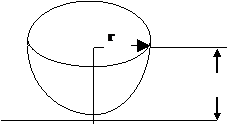 r =h
h
v = 2p×h3×/3 или v = 2p×r×3/3 r =h
h
v = 2p×h3×/3 или v = 2p×r×3/3
|
Пример выполнения задания №1.
Задан аппарат на рис. Л1.1, состоящий из трех фигур вращения.
Математическая формулировка задачи.
Параметры аппарата:
Высоты фигур h1, h2, h3; радиусы фигур r1=h1, r2, r3.
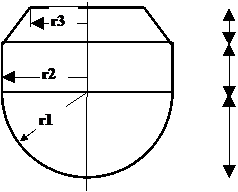 Используем формулы из табл. Л1.1а. для усеченного конуса, цилиндра и полусферы.
Используем формулы из табл. Л1.1а. для усеченного конуса, цилиндра и полусферы.
 Усеченный конус: v3= p×h3(r3 2 +r2 2 +r2×r3)/3 h3
Усеченный конус: v3= p×h3(r3 2 +r2 2 +r2×r3)/3 h3
 Цилиндр: v2= p×r2 2× h2
Цилиндр: v2= p×r2 2× h2
Полусфера: r1=h1 v1= 2×p×r1 3 /3 h2

|

h1


Рис. Л1.1. Технологический аппарат
Задание №2. Выписать условия индивидуального задания из табл. Л1.2, что и будет представлять математическую формулировку задачи (см. ниже пример для нулевого варианта). Знаком + указаны вычисляемые функции и диапазон изменения Х. Составить разветвляющийся алгоритм решения задачи.
Таблица Л1.2 — Варианты к заданию №2
| Функ- ция | sin(x) | cos(x) | tg(x) | eX | ln(x) | 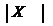
| 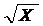
| X2.5 | В оста-льных |
| Усло- вие | 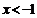
| 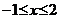
| 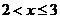
| 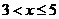
| 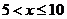
| 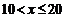
| 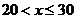
| 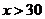
| слу- чаях |
| № вар. | |||||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | |||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + | ||||||
| + | + | + | + |
|

Примечание. " В остальных случаях" – принимается значение функции равное номеру варианта. Например, для десятого варианта это будет число 10.
Ориентировочный алгоритм – см. глава 1, рис. 1.3.
Задание № 3. Составить алгоритм вычисления суммы S членов ряда с заданной точностью Е и число его членов N, если задан общий член ряда an в табл. Л1. 3 (пример алгоритма см. глава 1, рис. 1.6).
Таблица Л1.3 — Варианты для задания №3
| № вар. | Общий член ряда | № вар. | Общий член ряда |
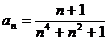
| 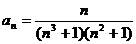
| ||
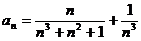
| 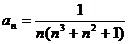
| ||
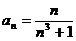
| 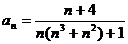
| ||
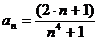
| 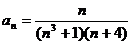
| ||
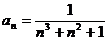
| 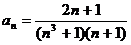
| ||
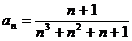
| 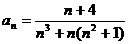
| ||
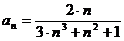
| 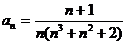
| ||
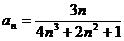
| 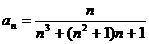
| ||
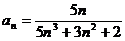
| 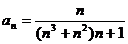
| ||
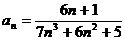
| 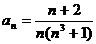
| ||
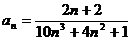
| 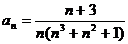
| ||
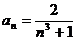
| 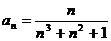
| ||
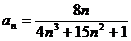
| 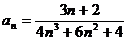
| ||
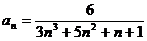
| 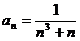
| ||
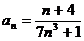
| 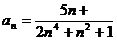
|
 2018-01-08
2018-01-08 667
667