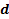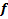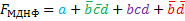Диаграмма Вейча для функции от 2 переменных

МДНФ:

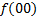
МКНФ:

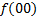
Диаграмма Вейча для функции от 3 переменных

МДНФ:

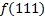
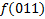
МКНФ:

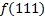
Диаграмма Вейча для функции от 4 переменных

МДНФ:

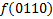
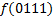
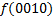
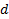
МКНФ:

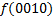
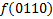
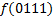
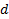
Наборы значений функции для МКНФ по отношению к МДНФ инвертируются.

Пусть дана таблица истинности логической функции:	1. Составим для данной функции диаграмму Вейча (МДНФ) и выделим интервалы: По данной диаграмме составим формулу:
2. Составим для данной функции диаграмму Вейча (МКНФ) и выделим интервалы: По данной диаграмме составим формулу:

 

Диаграмма Вейча для функции от 5 переменных

МДНФ:

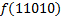
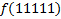
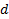
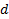
МКНФ:

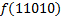
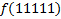
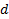
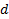
Минимизация частично определенных логических функций

В некоторых задачах нам известно, что определенные входные комбинации никогда не возникнут. В таком случае неопределенные значения интерпретируются так, как удобно.

Пусть дана частично определенная логическая функция:	1. Составим для данной функции диаграмму Вейча (МДНФ), считая неопределенные значения истинными. По данной диаграмме составим формулу:
2. Составим для данной функции диаграмму Вейча (МКНФ), считая неопределенные значения ложными. По данной диаграмме составим формулу:

 

Приведение минимизированной функции к заданному логическому базису

На примере .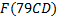

(МДНФ к базису ИЛИ-НЕ)

(МДНФ к базису И-НЕ)

(МКНФ к базису ИЛИ-НЕ)

(МКНФ к базису И-НЕ)

Лекция №6

Дешифраторы

Дешифратор – комбинационная схема, обладающая 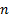-адресными входами, одним разрешающим входом и 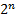выходами. На адресные входы подается двоичное число, которое в своем десятичном представлении задает номер выхода, на котором формируется значащий сигнал. Предназначена для преобразования 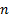-разрядного двоичного кода в унитарный двоичный код разрядности .

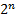В унитарном коде только один разряд из множества может принимать значение 1 (или 0). Это означает, что двоичное число (в своем десятичном представлении) задает номер того выхода, на котором появится 1 (или 0, если выходы инверсные).

Таблица истинности

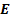
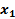
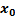
	x	x

Функциональная схема