Распределительное свойство умножения

(Метод «фонтанчика»)- И наоборот,

если выражение в скобках одинаковый

умножается на а, то скобки множитель

убираем, а каждое слагае- можно вынести

мое или вычитаемое умно- за скобки:

жаем на а: а∙(в+с)=а∙в+а∙с а∙в+а∙с= а∙(в+с)

а∙(с-у)=а∙с-а∙у; а∙в-а∙с= а∙(в-с)

а∙(в+с-у)=а∙в+а∙с-а∙у; а∙(в+с-у)=а∙в+а∙с-а∙у

Примеры: 7∙34-7∙4=7∙(34-4)=7∙30=210;

28∙18+2∙18=(28+2) ∙18=30∙18=540;

43∙2=(40+3) ∙2=40∙2+3∙2=80+6=86.

Свойства сложения и вычитания. Раскрываем скобки. 1.Если перед скобками ничего нет (они стоят в начале выражения) или перед скобками знак «+», то скобки просто убираем. (а+в)+с=а+в+с; а+(в+с)= а+в+с; (а-в)-с=а-в-с; а+(в-с)=а+в-с; и наоборот: а+в+с = а+(в+с). 2. Если перед скобками стоит знак минус, то скобки убираем, а знаки, которые были в скобках, меняем на противоположные. в - (2-а+с)=в-2+а-с; а +в-(с-у)=а+в-с+у   Умножение и деление натуральных чисел и его свойства. Степень числа. а∙0=0, а∙1=а, а∙а=а² (читают а в степени 2 или а в квадрате), а∙а∙а =а³ (читают а в степени 3 или а в кубе), и так далее, а∙а∙а∙а∙а =а⁵ (читают а в степени 5) 0²=0∙0=0 ноль в любой степени будет ноль, 1²=1∙1=1 один в любой степени будет один. На ноль делить нельзя! а:0=нельзя а:1=а, а:а=1, а:с+в:с=(а+в):с Фигуры Периметр –это сумма всех сторон Прямоугольник –это четырехугольник, у которого все углы прямые. Периметр Р=(а+в)∙2 Площадь S =а∙в Треугольник Р=а+в+с ∆ Квадрат –это прямоугольник у которого все стороны равны. Р =4∙а, S=а∙а=а² Окружность и круг Радиус R-это расстояние от центра О до любой точки окружности. R = ОА О ^R А Прямая -нет начала, нет конца. Луч –есть начало, нет конца. Отрезок - есть начало и конец. Координатный луч -это луч, у которого есть шкала (одинаковые деления) и указан единичный отрезок. ^{А Х} _{0 1 8} У точки А координата 8, это обозначают так: А(8). Прямоугольный параллелепипед У него все грани-прямоугольники. Его измерения- а,в,с (длина, ширина, высота) Объём V= а ∙ в∙с, Площадь поверхности S= (а∙в+в∙с+а∙с)∙2. _в ^{а   с} Куб У куба все грани- квадраты, все стороны равны. Объём V= а ∙ а∙а=а³, где а -сторона квадрата. 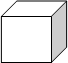Площадь поверхности S= (а∙а+а∙а+а∙а)∙2=6∙а².   ^а Углы. (измеряем в градусах транспортиром.)   Острый угол меньше прямого угла.

Прямой угол равен 90⁰.

Тупой угол больше 90⁰.

 

Развернутый угол равен 180⁰. ^А _В пишут: L АОВ. ^o Измеряют углы с помощью транспортира.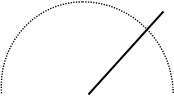

С

^135⁰

 

_{0⁰ 180⁰}

А В

L ABC = 135⁰.

Приближенные значения чисел. Округление чисел. Если следующее за разрядом, до которого нужно округлить, стоит число меньше 5,то все числа правее этого разряда заменяем нулями. (смотри таблицу) Если следующее за разрядом, до которого нужно округлить, стоит число больше 5 или =5, то к числу в этом разряде добавляем 1, а все числа правее этого разряда заменяем нулями. Нули стоящие после запятой в конце числа можно не писать. Округлим до десятых: 123,25≈123,30=123,3; 1,21≈1,2; 0,02≈0,00=0; 56,76556≈56,80000=56,8. Округлим до десятков: 123,25≈120,00=120; 6,21≈10,00=10; 0,02≈00,00=0; 56,76556≈60,00000=60. До сотых:56,6789≈56,6800=56,68; 0,0235≈0,0200=0,02. Деление с остатком 52 3 (делитель) 3 17(неполное частное) 22 21 52=17∙3+1 1(остаток) Дроби. 1 числитель 4 знаменатель. Числитель показывает, сколько частей взяли, а знаменатель на сколько или одинаковых частей разделили. У правильной дроби числитель меньше чем ^{0 ⅟4 1} знаменатель: 5, 12, 48, 1256. 6 13 59 189765 У неправильной дроби числитель равен или ^{0 ⅟4 1 5∕4} больше чем знаменатель: 5, 12, 48, 1256. 5 10 9 765 Правильная дробь всегда меньше 1, а неправильная дробь больше либо равна единице. 1454 4 4, 4 4. 565212 6 6, 12 12. Смешанная дробь - у неё есть и целая и дробная части, её можно превратить в неправильную дробь, и наоборот (делением в столбик). 5132 2 4 4, 5 5. _ 5 4 (знаменатель) _ 32 5 (знаменатель) 4 1 (целая часть) 30 6 (целая часть) 1 (числитель) 2 (числитель) Деление десятичной дроби на целое число. Если надо разделить число на десятичную дробь, то сначала переносим запятые у обоих чисел делителя и делимого – на одинаковое количество цифр вправо так, чтобы делитель стал целым числом. Затем делим десятичную дробь на целое число. 45,24: 0,5=452,4: 05=452,4: 5=452,40: 5=90,48 _452,40 5 45 90,48 _24 20 _40 40 При умножении десятичных дробей умножаем их как обычные числа, не обращая внимание на запятые, потом считаем, сколько чисел всего после запятых и в ответе отделяем запятой столько же цифр считая от конца. 25∙1,2=30,0=30; 1,98∙43,5=86,130=86,13 25 1,98 ^х 1,2 ^х 43,5 ₊ 50 ₊ 990 25__ ₊594 30,0 792 86,130   Наоборот: 1 1∙4+1526∙5+2 32 4 4 4, 5 5 5. (в числителе - целую часть умножаем на знаменатель и прибавляем числитель, знаменатель остается тот же). Основное свойство дроби– числитель и знаменатель дроби можно разделить или умножить на одно и то же число. 33∙412 5 5∙4 20. Действия с дробями. Сравнивать, отнимать и складывать можно дроби с одинаковыми знаменателями. При сложении (вычитании) дробей с одинаковыми знаменателями числители складывают (отнимают), знаменатель тот же. Примеры: 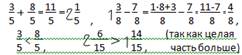Десятичные числа. 0,1=1/10; 0,5=5/10; 0,25=25/100; 1,234=1234/1000 (сколько чисел после запятой, столько нулей) Сложение и вычитание – запятая под запятой, запятую сносим, недостающие цифры заполняем нулями.(из целого числа делаем дробь 72=72,0) ₊123,543 _ 564,5 56,500 64,0 180,043 500,5 123,543+56,5=180,043; 564,5-64,5=500,5. Десятичная запись дробных чисел. Чтобы обыкновенную дробь записать в виде десятичной, надо числитель разделить на знаменатель в столбик. Когда целая часть заканчивается, запятую сносим. (Делить можно только на целое число.) Запишем дроби ¾, 25/8 в виде десятичных: 3:4=3,00:4=0,75; 25:8=25,000:8=3,125; _3,00 _ 4_ _25,000 _ 8 ___ 28 0,75 24 3,125 _20 _10 20 _ 8 0 _20 (так как 3<4 то 20 запятую сносим сразу) 0   Сравнение десятичных дробей.

1. Сравниваем целые части.
2. Если целые части равны, то начинаем сравнивать соответствующие числа, стоящие после запятой (недостающие – нули).

28,45>16,5; 0,99<1,56; 25,9<25,905; 12>11,3. Среднее арифметическое чисел– все числа сложить и разделить на их количество. Например, среднее арифметическое чисел 25; 35,7; 48; 12; 2,05 равно (25 + 35,7 + 48 +12 + 2,05):5=122,75:5=24,55. Средняя скорость V_СР=(S₁+S₂+S₃):(t₁+t₂+t₃)= общий путь:все время. Проценты. 1%=1/100 (1 процент равен одной сотой части числа) Пример1. В классе 25 учеников, 40% из них-девочки. Сколько девочек в классе? Решение: Всего детей – 100% девочки мальчики 40% 60% 25:100∙40=10 (девочек) Ответ: в классе 10 девочек.   Пример 2. На платье пошло 12 метров ткани, что составляет 15% всего рулона. Сколько метров ткани в рулоне? Решение: Всего ткани – 100% 15% 100-15= 85% ^{на платье осталось} 12:15∙100=80(м) Ответ: в рулоне 80 метров ткани.   Пример 3. Рабочий изготовил 20 деталей, а ему требуется изготовить 80 деталей. На сколько процентов он выполнил заказ? Решение: Всего 80 деталей – 100% 20 80-20=60 ^{изготовил осталось} 100:80∙20=25% Ответ: заказ выполнен на 25%. Формулы пути S = V∙t; V = S:t; t = S:V, S- это путь (расстояние), V- это скорость, t– это время.