2018-01-08
3752
Типовые задачи с решениями и для самостоятельного решения
По теме «Электроемкость и конденсаторы»
Типовые задачи с решениями
Задача 1. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью σ=0,2 мкКл/м2. Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?
| Дано: σ=0,2 мкКл/м2 d1=1мм d2=3мм | СИ 2·10-7 Кл/м2 10-3м 3·10-3м |
| ΔU-? |
Решение:
Заряд на пластинах конденсатора:
q = σ · S
Емкость плоского конденсатора:
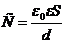
Напряжение на обкладках конденсатора: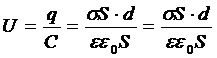 
.
Изменение разности потенциалов: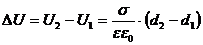 
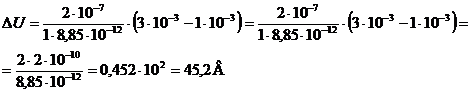
Ответ: ΔU=45,2 В.
Задача 2. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость C такой батареи конденсаторов равна 89пФ. Площадь S каждой пластины равна 100 см2. Диэлектрик — стекло. Какова толщина d стекла?
| Дано: Cобщ=89 пФ S=100 см2 ε=7 | СИ 89·10-12 Ф 10-2 м2 |
| d-? |
Решение:
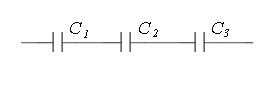
По условию задачи С1=С2=С3=С
|
|
|
Электроемкость батареи конденсаторов при их последовательном соединении:
; 
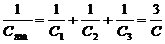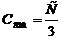
Электроемкость каждого плоского конденсаторы вычисляется по формуле:
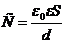
Тогда для батареи из трех конденсаторов: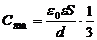 
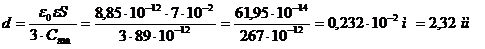
Ответ: d=2,3мм.
Задача 3. Конденсаторы электроемкостями C1=10 нФ, С2=40 нФ, C3=2нФ и C4=30 нФ соединены так, как это показано на рисунке. Определить электроемкость C соединения конденсаторов
| Дано: C1=10 нФ C2=40 нФ C3=2 нФ C4=30 нФ | СИ 10·10-9 Ф 40·10-9 Ф 2·10-9 Ф 30·10-9Ф |
| С -? |
Решение:
Конденсаторы С1 и С2 (а так же С3 и С4) соединены последовательно, поэтому
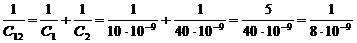; С12= 8·10-9 Ф=8 пФ
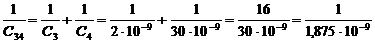; С34=1,875·10-9 Ф=1,875 пФ
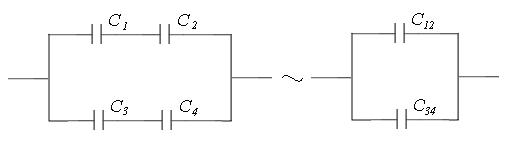
Конденсаторы С12 и С34 соединены параллельно, поэтому
С= С12+ С34=8+1,875=9,875нФ
Ответ: С=9,875 нФ.
Задача 4. Конденсаторы электроемкостями C1=0,2 мкФ, C2=0,6 мкФ, C3=0,3 мкФ, C4=0,5 мкФ соединены так, как это указано на рисунке. Разность потенциалов U между точками А и В равна 320 В. Определить разность потенциалов Ui и заряд Qi на пластинах каждого конденсатора (i=1, 2, 3, 4).
| Дано: C1=0,2 мкФ C2=0,6 мкФ C3=0,3 мкФ C4=0,5 мкФ UАВ=320 В | СИ 2·10-7 Ф 6·10-7 Ф 3·10-7 Ф 5·10-7 Ф 320 В |
| Ui-? Qi-? |
Решение:
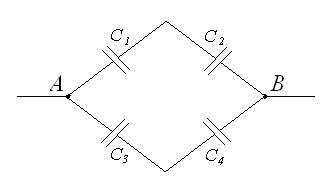
Разность потенциалов между точками А и В:
UAB=U1+U2=U3+U4
Конденсаторы С1 и С2 (а так же С3 и С4) соединены последовательно, поэтому
q1=q2 и q3=q4
q=CU, тогда C1U1= C2U2, отсюда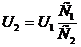 
;
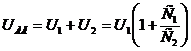
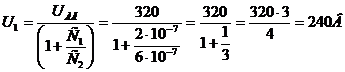
U2= UAB –U1=320-240=80 В
Аналогично для С3 и С4:
C3U3= C4U4, отсюда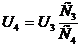 
;
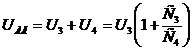
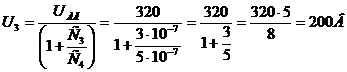
U4= UAB –U3=320-200=120 В
Найдем заряд qi на каждом конденсаторе, учитывая, что q1=q2 и q3=q4:
q1= q2=C1·U1=2·10-7·240=480·10-7Кл=48·10-6 Кл=48 мкКл
q3= q4=C3·U3=3·10-7·200=600·10-7Кл=60·10-6 Кл=60 мкКл
Ответ: q1=q2=48 мкКл, q3=q4=60 мкКл, U1=240В, U2=80В, U3=200В, U4=120В.
Задача 5. Два конденсатора электроемкостями C1=3 мкФ и C2=6 мкФ соединены между собой и присоединены к батарее с ЭДС ε=120 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между их обкладками, если конденсаторы соединены: 1) параллельно; 2) последовательно.
|
|
|
| Дано: C1=3 мкФ C2=6 мкФ ε=120 В | СИ 3·10-6 Ф 6·10-6 Ф |
| Ui-? Qi -? при параллельном и последовательном соединениях конденсаторов |
Решение:
1) Рассмотрим последовательное соединение конденсаторов:
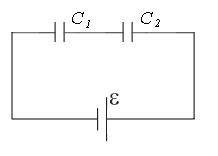
Общая емкость конденсаторов при последовательном соединении:
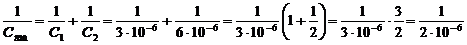
Собщ=2·10-6 Ф
При последовательном соединении заряды на конденсаторах одинаковы:
q=q1=q2
q=q1=q2 =Cобщ·ε = 2·10-6 ·120 = 240·10-6 Кл = 240 мкКл
Напряжения на конденсаторах найдем, используя формулу q=CU
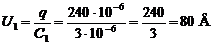
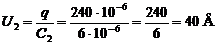
2) Рассмотрим параллельное соединение конденсаторов:
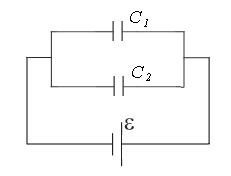
При параллельном соединении конденсаторов напряжения на них равны:
ε=U1=U2 =120 В
Заряд каждого конденсатора найдем с помощью формулы q=CU:
q1 = C1·U1 = 3·10-6·120 = 360·10-6 Кл = 360 мкКл
q2 = C2·U2 = 6·10-6·120 = 720·10-6 Кл = 720 мкКл
Ответ:
1) при последовательном соединении q1=q2=240 мкКл, U1=80В, U2=40В;
2) при параллельном соединении U1=U2=120В, q1=360мкКл, q2=720мкКл.
