ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ №2
( – номер по списку;
– номер по списку; 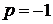 )
)
1. Найдите линейную зависимость векторов  ,
, 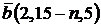 ,
,  ,
,  . Тут
. Тут 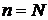 .
.
2. Даны векторы 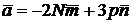 и
и  , где
, где 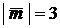 ,
, 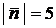 ,
, 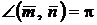 . Найти: а)
. Найти: а) 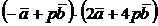 ; б)
; б) 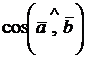 ; в)
; в)  ; г) площадь треугольника, построенного на векторах
; г) площадь треугольника, построенного на векторах 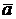 и
и  .
.
3. По координатам 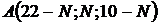 ,
, 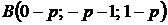 ,
,  для указанных векторов найти: а) скалярное произведение векторов
для указанных векторов найти: а) скалярное произведение векторов 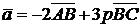 и
и  ; б) длину вектора
; б) длину вектора 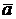 ; в) координаты точки М, делящей направленный отрезок АВ в отношении
; в) координаты точки М, делящей направленный отрезок АВ в отношении 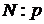 ; в) проверить, ортогональны ли векторы
; в) проверить, ортогональны ли векторы 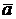 и
и  ; г) проверить, коллинеарны ли векторы
; г) проверить, коллинеарны ли векторы 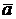 и
и  ; д) проверить, компланарны ли векторы
; д) проверить, компланарны ли векторы 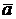 ,
,  и
и 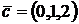 ; е) вычислить объем тетраэдра с вершинами в точках A, B, C и
; е) вычислить объем тетраэдра с вершинами в точках A, B, C и 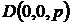 .
.
4. Даны координаты вершин  :
: 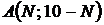 ,
, 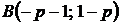 ,
,  . Найти:
. Найти:
1) уравнение стороны 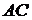 ;
;
2) уравнение медианы 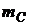 ;
;
3) уравнение высоты 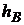 , опущенной из вершины
, опущенной из вершины  ;
;
4) длину высоты 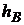 ;
;
5) уравнение биссектрисы 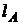 , проведенной из вершины А;
, проведенной из вершины А;
6) точку пересечения медианы 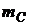 и высоты
и высоты 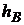 ;
;
7) косинус угла между 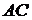 и медианой
и медианой 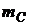 ;
;
8) уравнение прямой, проходящей через вершину  параллельно прямой
параллельно прямой 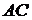 .
.
5. Даны четыре точки: 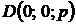 ,
, 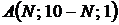 ,
,  ,
, 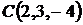 . Найти:
. Найти:
1) уравнения прямых 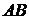 ,
, 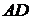 ;
;
2) уравнения плоскостей 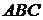 ,
, 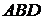 ;
;
3) уравнение перпендикуляра  , опущенного из точки
, опущенного из точки 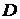 на плоскость
на плоскость 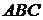 ;
;
4) длину высоты  ;
;
5) косинус угла между прямыми 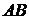 и
и 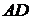 ;
;
6) синус угла между прямой 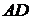 и плоскостью
и плоскостью 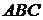 ;
;
7) косинус угла между плоскостями 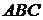 и
и 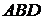 ;
;
8) уравнение прямой, проходящей через точку 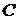 перпендикулярно плоскости
перпендикулярно плоскости 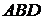 ;
;
9) уравнение плоскости, проходящей через точку 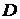 перпендикулярно прямой
перпендикулярно прямой 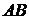 .
.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ
Задача 1. Написать уравнение касательных:
1) к эллипсу  , проведенных в точке на линии
, проведенных в точке на линии  ;
;
2) к гиперболе 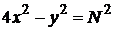 , проведенных в точке на линии
, проведенных в точке на линии  ;
;
3) к параболе  , проведенных в точке на линии
, проведенных в точке на линии 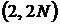 .
.
Задача 2. Составить каноническое уравнение эллипса и схематически изобразить, зная, что:
1) полуоси ее соответственно равны 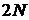 и
и  ;
;
2) расстояние между фокусами равно  и большая полуось равна
и большая полуось равна  ;
;
3) большая полуось равна 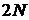 и эксцентриситет
и эксцентриситет 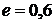 ;
;
4) малая полуось равна  и эксцентриситет
и эксцентриситет 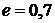 ;
;
5) сумма полуосей равна 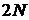 и расстояние между фокусами тоже равно
и расстояние между фокусами тоже равно 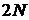 ;
;
6) она проходит через точку 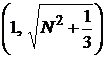 и малая полуось равна
и малая полуось равна  .
.
Задача 3. Составить каноническое уравнение гиперболы и схематически изобразить, зная, что:
1) полуоси его соответственно равны  и
и 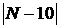 ;
;
2) расстояние между фокусами равно  и действительная полуось равна
и действительная полуось равна 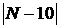 ;
;
3) действительная полуось равна 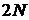 и эксцентриситет
и эксцентриситет  ;
;
4) мнимая полуось равна  и эксцентриситет
и эксцентриситет  ;
;
5) сумма полуосей равна 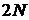 и расстояние между фокусами тоже равно
и расстояние между фокусами тоже равно  ;
;
он проходит через точку 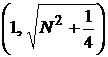 и мнимая полуось равна
и мнимая полуось равна  .
.
Задача 4. Привести к каноническому виду, определить вид и схематически изобразить уравнение:
а) поверхности (номер задания соответствует номеру варианта)
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6) 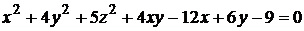 ;
;
7) 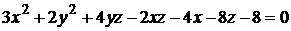 ;
;
8) 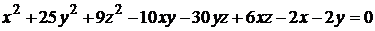 ;
;
9)  ;
;
10) 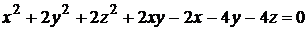 ;
;
11) 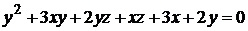 ;
;
12) 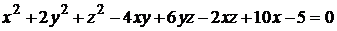 ;
;
13) 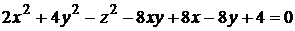 ;
;
14) 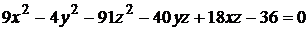 ;
;
15)  ;
;
16) 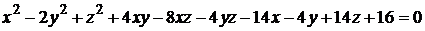 ;
;
17) 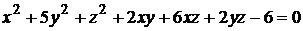 ;
;
18) 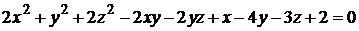 ;
;
19) 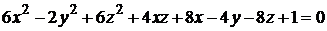 ;
;
б) кривой (номер задания соответствует номеру варианта)
1) 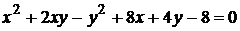 ;
;
2) 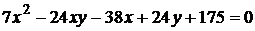 ;
;
3)  ;
;
4) 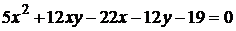 ;
;
5)  ;
;
6) 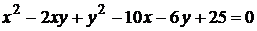 ;
;
7) 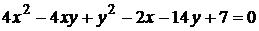 ;
;
8) 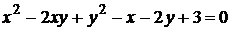 ;
;
9) 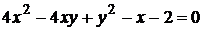 ;
;
10) 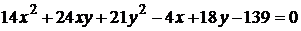 ;
;
11) 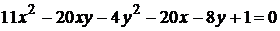 ;
;
12) 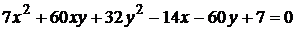 ;
;
13) 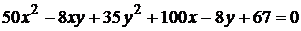 ;
;
14) 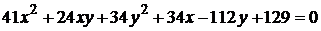 ;
;
15) 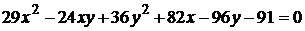 ;
;
16) 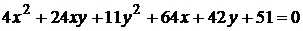 ;
;
17) 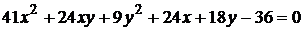 ;
;
18) 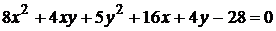 ;
;
19) 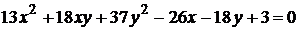 .
.
 2018-01-08
2018-01-08 162
162






