Теоретические сведения

ЛАБОРАТОРНАЯ РАБОТА № 2

 

ИЗМЕРЕНИЕ ДЕТАЛЕЙМИКРОИНСТРУМЕНТАМИ

тема

 

 

Студент ________ А.В.Терехова

подпись, дата инициалы, фамилия

 

Преподаватель __________ Е.С. Турышева

подпись, дата инициалы, фамилия

 

 

Красноярск 2012

Цели работы: изучить устройство микроинструментов; освоить методы измерения деталей с помощью микроинструментов.

Теоретические сведения

Метод измерения деталей с помощью микрометрических инструментов - абсолютный. Верхний предел измеряемых величин для каждого типа микрометрического инструмента устанавливается соответствующим государственным стандартом. Все микрометрические инструменты (кроме микрометрического нутромера) имеют трещотку – механизм, обеспечивающий определенное измерительное усилие. Погрешность измерения состоит из погрешности инструмента, погрешности метода измерения и др. Основная погрешность (инструментальная) микрометров обычно не превышает ±5 мкм (±0,005 мм). Под ней понимается величина отклонения результата измерения от эталона, полученная при поверке инструмента.

Микрометры общего назначения (ГОСТ 6507-90 « Микрометры.Техни-ческие условия») подразделяются на следующие типы:

МК – гладкие (для установления наружных размеров изделий);

МЗ – зубомерные (для контроля длины общей нормали зубчатых колес);

МТ – трубные (для измерения толщины стенок труб);

МП – проволочные (для измерения проволоки).

Пример условного обозначения гладкого микрометра 1-го класса точности с диапазоном измерения 25-50 мм: микрометр МК-50-1 ГОСТ 6507-90.

Микрометры со вставками используются для специальных измерений и по ГОСТ 4380-86 «Микрометры со вставками. Технические условия»подраз-деляютсяна:

МВМ – для измерения среднего диаметра метрической и дюймовой резьбы;

МВТ – для измерения среднего диаметра трапецеидальной резьбы;

МВП– с плоскими вставками (для измерения деталей из мягких материалов).

Пример условного обозначения резьбового микрометра с диапазоном измерений 0-25 мм: микрометр МВМ 0-25 ГОСТ 4380-93.

Микрометрические глубиномеры (ГОСТ 7470-92 «Глубиномеры микрометрические.Технические условия») изготавливаются 1-го и 2-го классов точности с диапазонами измерений 0-100, 0-150 мм.

Диапазоны измерений обеспечиваются набором сменных измерительных стержней. Пример условного обозначения микрометрического глубиномера с диапазоном измерений 0-100 мм: глубиномер ГМ 100 ГОСТ 7470-92.

Микрометрические нутромеры (ГОСТ 10-88 «Нутромеры микро-метрические.Технические условия») выпускаются с пределами измерения 0-75; 75-175; 75-600; 150-1250; 600-2500; 1250-4000; 2500-6000 мм.Диапазон измерений достигается за счет сменных удлинительных стержней. Микрометрический нутромер с верхним пределом измерений 175 ммобозначается следующим образом: нутромер НМ175 ГОСТ 10-88.

На рис.1 –4 показаны микрометрические инструменты. Их выбирают по типу объекта измерения, пределам измерения и классу точности, в зависимости от размера и допускаемой погрешности измерения по ГОСТ 8.051-81.

Гладкие микрометры с диапазоном измерений 25-50, 50-75, 75-100 мм и др. настраиваются на нуль аналогично, но при этом используется установочная мера, равная нижнему пределу измерениямикрометра: 25, 50, 75 мм и др. соответственно. После соприкосновения измерительных поверхностей микрометра с установочной мерой нулевой штрих круговой шкалы барабана должен совпасть с продольным штрихом стебля. Установочные меры поставляются в комплекте с микрометрами.

Рисунок 1 – Гладкий микрометр

 

Рисунок 2 – Микрометрический глубиномер

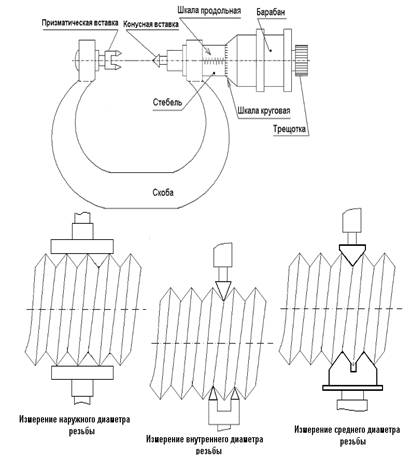
Рисунок 3– Микрометр зубомерный

 

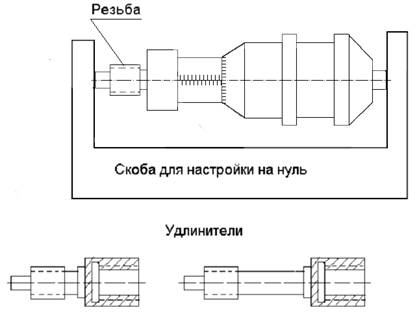
Рисунок 4– Микрометрический нутромер

Ход работы

Оборудование и приборы: зубомерные микрометры; детали.

Таблица 1 – Средства измерения – микроинструменты

Инструмент	Тип)модель)	Диапазон измерения	Цена деления	Обозначение
Микрометр	МК	25-50 мм	0,01мм	Микрометр МК-50-1 ГОСТ 6507-90

 

Фактические размеры диаметра с восходящим рядом чисел партии деталей

n = 100 шт. показаны в таблице 2.

Таблица 2 – Действительные размеры деталей

Размеры в мм

44,57	44,54	44,50	44,97	44,53
44,66	44,53	44,99	44,97	44,54
44,64	44,52	44,57	44,97	44,63
44,69	44,53	44,56	44,54	44,51
44,66	44,50	44,54	44,55	44,66
44,51	44,65	44,52	44,58	44,99
44,55	44,54	44,52	44,70	44,56
44,50	44,69	44,60	44,51	44,97
44,53	44,61	44,53	44,51	44,61
44,65	44,52	44,99	44,61	44,55
44,98	44,63	44,50	44,52	44,52
44,55	44,70	44,98	44,90	44,65
44,54	44,59	44,52	44,59	44,58
44,97	44,52	44,97	44,69	44,51
44,67	44,53	44,50	44,61	44,55
44,59	44,52	44.89	44,50	44,50
44,66	44,95	44,97	44,54	44,50
44,67	44,63	44,51	44,56	44,59
44,60	44,50	44,97	44,61	44,53
44,54	44,57	44,99	44,58	44,57

X_max=44,99 мм; X_min= 40,84 мм.

Весь диапазон X_max... X_minрезультатов наблюдений разделим на 10 интервалов шириной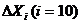

Число интервалов выбирается в зависимости от числа наблюдений согласно рекомендациям таблицы 3.

Таблица 3 – Зависимость числа интервалов от числа наблюдений

n	r
40 – 100	7 – 9
100 – 500	8 – 12
500 – 1000	10 – 16
1000.....10000	12 – 22

Принимаем интервал рассеивания равным 0,05 мм и разбиваем все размеры на группы, как показано в таблице 4.

Таблица 4 – Распределение действительных размеров по интервалам

Интервалы	Частота, n	Вероятность,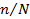
44,50 до 44,55 свыше 44,55 до 44,60 44,60 до 44,65 44,65 до 44,70 44,70 до 44,75 44,75 до 44,80 44,80 до 44,85 44,85 до 44,90 44,90 до 44,95 44,95 до 45,00		0,44 0,16 0,11 0,12 0,01 0,02 0,14
Σn = 100

 

Вероятность (частость) есть отношение количества деталей данного интервала (n) к общему количеству (N) деталей исследуемой партии 100 шт.

(1)

Сумма вероятностей составляет целую единицу, т.е. 100% всех деталей партии.

Откладывая в масштабе по оси абсцисс размеры деталей или интервалы, апо оси ординат – вероятность (частость) для каждого интервала размеров и соединяя полученные точки плавной линией, получим кривую распределения.

 

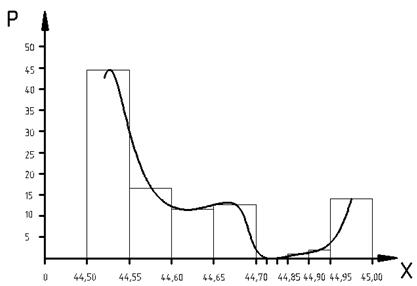
Рисунок 5 – Гистограмма распределения результатов измерений

Кривая нормального распределения определяется функцией

, (2)

где х – случайная величина;

m_х – математическое ожидание случайной величины, т.е. значение абсциссы, соответствующее вершине кривой Ymax. Mода кривой m_х – есть центр группирования (распределения) и вместе с тем является средней арифметической распределения / Х_ср /.

s – среднеквадратичное отклонение.

Точность обработки партии деталей будет характеризоваться средним вероятным размером /Х_ср/, средним квадратическим отклонением.

Среднее арифметическое значение действительных размеров определяется уравнением.

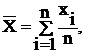(3)

где x_i – результат i – го наблюдения

n – число наблюдений.

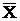=44,6368

 

 

Среднее квадратичное отклонение погрешности (СКО):

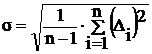, (4)

где .– отклонение результата отдельного наблюдения от среднего арифметического равно: 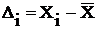. (5)

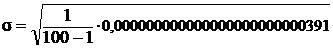0,0000000000000628

Среднее квадратичеcкое отклонение позволяет определить наибольшее рассеивание размеров, которое практически следует учитывать (границы поля рассеивания). В качестве такого предела приняли ± 3s = 6 s.(3s=0,000000000000188528)

 

Вероятность получения размера в пределах ±3s составляет

 

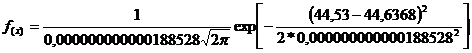2116623651850,93* (-160457286292006000000000,0) = 0