Математические модели элементов электрической цепи

В основе теории электрических цепей лежит принцип моделирования. При этом реальные электрические цепи заменяются некоторой идеализированной моделью, состоящей из взаимосвязанных идеализированных элементов. Последние представляют собой простые модели, используемые для аппроксимации (приближения) свойств простых физических элементов или физических явлений. К простейшим идеализированным элементам модели электрической цепи относятся независимые и зависимые источники (активные элементы) и пассивные элементы: резистивное сопротивление, индуктивность и емкость.

Математической моделью электрической цепи обычно называют систему уравнений, описывающую модель электрической цепи.

Резистивным сопротивлением называют элемент, обладающим только свойством необратимого рассеивания энергии. Условное обозначение резистивного элемента показано на рис. 3.1, а.

Рис. 3.1. Резистивное сопротивление

Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:

, . (3.1)

Коэффициенты пропорциональности и называются соответственно сопротивлением и проводимостью элемента и являются его количественной характеристикой. Зависимость (3.1) называется вольт-амперной характеристикой (ВАХ) резисторного сопротивления. Если , то ВАХ – линейна (рис. 3.2, б), если или , то ВАХ – нелинейна (рис. 3.2, а).

 

Рис. 3.2. Вольт амперные характеристики
резисторов с нелинейным (а) и линейным (б) сопротивлениями

Мощность в резистивном сопротивлении определяется согласно выражению:

.

Мощность в резистивном сопротивлении всегда положительна, так как оно только потребляет энергию, преобразуя ее в тепло.

Индуктивным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное графическое обозначение индуктивного элемента показано на рис. 3.3.

Рис. 3.3. Условное графическое обозначение индуктивного элемента

Математическая модель, описывающая свойства индуктивного элемента, определяется соотношением

, , (3.2)

где - потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку

Коэффициент пропорциональности называется индуктивностью. Он имеет положительное значение и является количественной характеристикой индуктивного элемента. Если величина постоянна, то зависимость (3.2) (вебер–амперная характеристика) линейна и соответствует линейному индуктивному элементу. Если же зависит от электрического режима цепи (тока или напряжения), то зависимость (3.2) нелинейная и соответствует нелинейному элементу индуктивности.

Связь между напряжением и током на индуктивном элементе определяется согласно закону электромагнитной индукции:

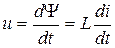, , (3.3)

т.е. напряжение на индуктивном элементе пропорционально скорости изменения тока в нем. Отсюда следует важное практическое приложение: при протекании через L постоянного тока свойства индуктивного элемента (катушки индуктивности) эквивалентны коротко замкнутому (КЗ) участку цепи т.е. U_L =0.

Зависимость тока от приложенного напряжения в индуктивном элементе определяется зависимостью:

,

где – константа интегрирования, численно равная начальному току, протекающему через катушку индуктивности.

Мощность электрических колебаний в индуктивном элементе:

,

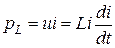т.е. может быть как положительной (при совпадении направлений и ), так и отрицательной. Причем в первом случае () мощность потребляется индуктивным элементом, а во втором случае () – отдается.

Энергия, запасенная в индуктивном элементе к моменту времени t, определяется зависимостью:

,

т.е. всегда положительна.

Емкостным элементом называют идеализированный элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.5. На практике используются дольные единицы: , , .

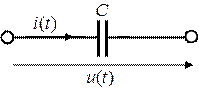Рис. 3.4. Условное графическое обозначение емкостного элемента

Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулоновской характеристикой:

, .

Коэффициент пропорциональности называется емкостью и является количественной характеристикой емкостного элемента. Измеряется емкость в фарадах (Ф). На практике используются дольные единицы: , , .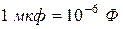

Если постоянная, то вольт-кулоновская характеристика линейная. Если же , то характеристика нелинейная. Между током и напряжением на емкостном элементе существует зависимость, определяемая равенством:

, ,

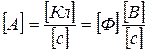т.е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. Отсюда следует также важное практическое приложение: при постоянном напряжении емкостной элемент по своим свойствам эквивалентен разрыву цепи т.е. .

Зависимость напряжения от протекающего тока в емкостном элементе определяется зависимостью:

,

где – константа интегрирования, численно равная начальному напряжению на конденсаторе.

Мощность электрических колебаний в емкостном элементе:

,

т.е. может быть как положительной (при совпадении направлений и ), так и отрицательной. Причем в первом случае () мощность потребляется емкостным элементом, а во втором случае () – отдается.

Энергия, запасенная в емкостном элементе к моменту времени t, определяется зависимостью:

,

т.е. всегда положительна.

Активные элементы. Активными элементами электрической цепи являются зависимые и независимые источники электрической энергии. К независимым источникам относятся аккумуляторы, электрогенераторы, термоэлементы и т.д. К зависимым источникам относятся транзисторы, операционные усилители и т.д.

Независимые источники можно представить в виде двух моделей – источника напряжения и источника тока.

Независимым источником напряжения называют идеализированный двухполюсный элемент, напряжение (э.д.с.) на зажимах которого не зависит от протекающего через него тока (внутренне сопротивление равно нулю). Вольт-амперная характеристика источника напряжения представляет собой прямую линию, параллельную оси токов. В теории электрических цепей реальные источник напряжения заменяют некоторой идеализированной моделью (рис. 3.5, а), состоящей из комбинации идеального источника напряжения и его внутреннего сопротивления.

Рис. 3.5. Источник напряжения (ЭДС)

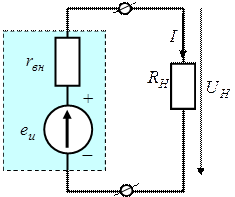В электрической цепи, изображенной на рис. 3.6, ток определяется законом

Рис. 3.6. Реальный источник ЭДС с нагрузкой

Ома для замкнутой цепи, при этом падение напряжения на нагрузке может быть определено так:

,

и при :

,

и источник напряжения приближается к идеальному источнику напряжения.

Независимым источником тока называют идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах (внутренне сопротивление бесконечно велико). Условное обозначение источника тока показано на рис. 3.7. Источник тока полностью характеризуется своим задающим током . Внутренняя проводимость источника тока равна нулю (внутренне сопротивление бесконечно велико) и ВАХ представляет собой прямую линию параллельную оси напряжений (рис. 3.7, в). Такой источник способен отдавать во внешнюю цепь бесконечно большую мощность и является идеализацией реальных независимых источников.

Рис. 3.7. Источник тока

Свойства реальных источников с конечным внутренним сопротивлением можно моделировать с помощью независимых источников напряжения и тока с дополнительно включенными резистивными сопротивлениями 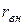или проводимостью (рис. 3.5, б; рис. 3.7, б). Напряжение и отдаваемый ток этих источников уже будет зависеть от параметров подключаемой к ним цепи, а их ВАХ будут иметь тангенс угла a наклона, пропорциональны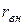й и соответственно (рис. 3.5, в; рис. 3.7, в).

При этом, чем меньше внутренне сопротивление или проводимость реальных источников напряжения и тока по сравнению с сопротивлением или проводимостью нагрузки, тем ближе их свойства к идеальным источникам.

Однако свойства целого ряда электронных устройств нельзя описать моделью соединенных между собой указанных выше независимых источников и пассивных двухполюсных элементов. К числу таких устройств относятся электронные лампы, транзисторы, операционные усилители и другие электронные приборы. Это так называемые зависимые или управляемые источники, которые играют важную роль в генерации и усилении электрических колебаний.

В ряде случаев использование принципа дуальности позволяет облегчить исследование процессов в цепи. Так, если известны основные соотношения, описывающие процессы в некоторой цепи, то соответствующие соотношения для дуальной цепи могут быть получены без вывода, на основании использования свойства дуальности.

Рассматривая соотношения (табл. 3.1), приходим к заключению, что выражения, соответствующие попарно сопротивлению и проводимости, емкости и индуктивности, имеют подобную структуру. Если в выражениях, описывающих основные соотношения для сопротивления, заменить на , на , на , то получатся основные соотношения для проводимости. Аналогично, выражения, описывающие основные соотношения для емкости и индуктивности, могут быть получены одно из другого путем замены на , на , на .

Таблица 3.1

Ток, напряжение, мощность и энергия идеализированных пассивных элементов

Тип идеализированного элемента	Основные уравнения для:
тока	напряжения	мгновенной мощности	энергии
Сопротивление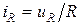
Проводимость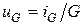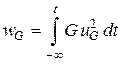
Емкость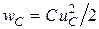
Индуктивность

 

Элементы, для которых основные соотношения имеют одинаковую структуру и могут быть получены одно из другого путем таких замен, называются дуальными. Таким образом, емкость и индуктивность, сопротивление и проводимость (попарно) являются дуальными элементами.