Теорема Куна-Таккера
Теорема Куна-Таккера была сформулирована в 1951 г. Рассмотрим задачу выпуклого программирования
 , (з)
, (з)
где  – линейное пространство,
– линейное пространство,  – выпуклые функции на
– выпуклые функции на  ,
,  – выпуклое подмножество
– выпуклое подмножество  .
.
Для задачи (з) введем понятие функции Лагранжа:
 .
.
Здесь  – множители Лагранжа. (Ограничение
– множители Лагранжа. (Ограничение 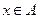 в функцию Лагранжа не включается).
в функцию Лагранжа не включается).
Теорема Куна-Таккера. 1. Пусть  . Тогда, существуют
. Тогда, существуют  , «нерон», такие, что выполняются
, «нерон», такие, что выполняются
а) принцип минимума
 ;
;
б) условие неотрицательности
 ;
;
в) условие дополняющей нежесткости
 .
.
2. Если  , то условий а)-в) достаточно для того, чтобы допустимая точка
, то условий а)-в) достаточно для того, чтобы допустимая точка  .
.
3. Для того, чтобы  , достаточно выполнения условия Слейтера, т. е. существования точки
, достаточно выполнения условия Слейтера, т. е. существования точки  , для которой
, для которой  .
.
Комментарии к теореме Куна-Таккера.
1.Соотношение а) отражает мысль Лагранжа в наиболее завершенной форме: если  доставляет минимум в задаче с ограничениями (типа неравенств), то эта же точка доставляет минимум функции Лагранжа (в задаче без тех ограничений, которые включены в функцию Лагранжа).
доставляет минимум в задаче с ограничениями (типа неравенств), то эта же точка доставляет минимум функции Лагранжа (в задаче без тех ограничений, которые включены в функцию Лагранжа).
2. Соотношения б) и в) характерны для задач с неравенствами.
 Доказательство теоремы Куна-Такккера опирается на теорему отделимости для конечномерного случая (д-во в АТФ, п. 1.3.4.).
Доказательство теоремы Куна-Такккера опирается на теорему отделимости для конечномерного случая (д-во в АТФ, п. 1.3.4.).
Конечномерная теорема отделимости. Пусть  – выпуклое подмножество в
– выпуклое подмножество в 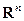 , не содержащее точки
, не содержащее точки  . Тогда существует набор чисел
. Тогда существует набор чисел  таких, что для
таких, что для 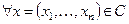 выполняется неравенство
выполняется неравенство  .
.
Другими словами гиперплоскость 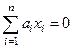 , проходящая через 0, делит
, проходящая через 0, делит 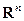 на две части, в одной из которых целиком лежит
на две части, в одной из которых целиком лежит  .
.

Двумерная иллюстрация: можно провести через 0 гиперплоскость таким образом, что множество  останется по одну сторону:
останется по одну сторону:  (
(
 ).
).

Если  – невыпуклое множество, этого сделать было бы нельзя.
– невыпуклое множество, этого сделать было бы нельзя.
Перейдем к доказательству теоремы Куна-Таккера. Докажем пункт 1.
1. Н е о б х о д и м о с т ь. Пусть  . Будем считать, что
. Будем считать, что  , – иначе возьмем новую функцию
, – иначе возьмем новую функцию  .
.
Введем множество
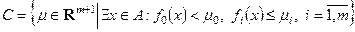 ,
,
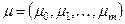 .
.
Дальнейшую часть доказательства разбиваем на несколько этапов.
I. Множество  – непусто.
– непусто.
Возьмем  и в качестве
и в качестве 
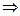
 – очевидно, так как у нас
– очевидно, так как у нас  =0,
=0,
 – очевидно, так как у нас
– очевидно, так как у нас  (см. (з)).
(см. (з)).
II. Множество  – выпукло.
– выпукло.
Возьмем  и
и  . Тогда
. Тогда  и
и 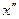 такие элементы из
такие элементы из  (
( ), что (см. множество
), что (см. множество  ):
):
 ,
, 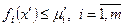 ,
,
 ,
,  .
.
Надо доказать, что  такая, для которой выпуклая комбинация
такая, для которой выпуклая комбинация  будет принадлежать множеству
будет принадлежать множеству  :
:  .
.
Положим  . Тогда,
. Тогда,  , поскольку
, поскольку  – выпукло, а так как все функции выпуклы, то
– выпукло, а так как все функции выпуклы, то

т. е. точка 
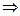
 – выпукло.
– выпукло.
III. Точка  не принадлежит
не принадлежит  .
.
Действительно, если  , то
, то  такая, что
такая, что  ,
,  . Но из этих неравенств следует, что
. Но из этих неравенств следует, что  не является решением задачи (з). Значит,
не является решением задачи (з). Значит,  .
.
Итак,  – выпукло,
– выпукло,  ,
,  . Следовательно, можно применить конечномерную теорему отделимости, согласно которой
. Следовательно, можно применить конечномерную теорему отделимости, согласно которой  такие, что
такие, что
 . (*)
. (*)
Из I, II, III 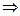 (*).
(*).
IV. Докажем условие неотрицательности:  .
.
Возьмем в качестве  , где
, где  и 1 стоит на
и 1 стоит на  -м месте.
-м месте. 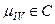 (см. п. I).
(см. п. I).
 подставим в (*)
подставим в (*) 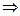

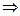
 . Так как
. Так как  – произвольно, то
– произвольно, то  .
.
V. Докажем условие дополняющей нежесткости:  .
.
а). Если  , то условие очевидно.
, то условие очевидно.
б). Если  , то
, то  (см. формулировку (з)).
(см. формулировку (з)).
Возьмем  , где
, где  и
и  стоит на
стоит на  -м месте.
-м месте.
 – достаточно взять точку
– достаточно взять точку  в качестве точки
в качестве точки 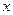 в А:
в А:  – очевидно, так как
– очевидно, так как  ;
;  при
при  и
и 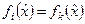 при
при  – очевидно.
– очевидно.
 подставим в (*)
подставим в (*) 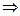

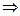
 ,
,
причем  . В силу произвольности
. В силу произвольности  получаем
получаем  , но
, но  (см. IV, т. е. условие б))
(см. IV, т. е. условие б)) 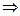
 , если
, если 
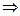
 .
.
VI. Докажем принцип минимума.
Пусть 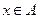 ,
,  ,
,  . Покажем, что
. Покажем, что  .
.  – очевидно,
– очевидно,  – очевидно
– очевидно 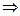
 .
.
Подставим  в (*)
в (*) 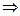

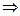

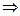 (в силу произвольности
(в силу произвольности  )
) 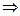
 , так как
, так как  =0 по предположению,
=0 по предположению,  – по условию дополняющей нежесткости. Отсюда следует принцип минимума:
– по условию дополняющей нежесткости. Отсюда следует принцип минимума:  .
.
Итак, пункт 1 теоремы Куна-Таккера доказан.
Докажем пункт 2.
2. Д о с т а т о ч н о с т ь. Пусть  . Но тогда
. Но тогда



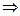
 .
.
В логической цепочке присутствуют пункты а), б), в).
3. Докажем утверждение 3 от противного.
Пусть условие Слейтера выполняется (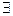
 :
:  ), но все-таки
), но все-таки  . Приведем к противоречию.
. Приведем к противоречию.
 ,
,
так как, в силу условия «нерон», не все 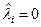 ,
,  . Тогда,
. Тогда,

 .
.
А это противоречит принципу минимума.
Теорема доказана. 
Пример.  . Решим поставленную задачу, используя теорему Куна-Таккера. Функция Лагранжа:
. Решим поставленную задачу, используя теорему Куна-Таккера. Функция Лагранжа:
 .
.
Выпишем условия, определяющие решение данной задачи выпуклого программирования:

 , так как выполняется условие Слейтера:
, так как выполняется условие Слейтера: 
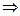 Можно положить
Можно положить  .
.
Из соотношений (1), (2) следует, что 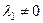 и
и 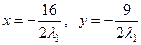 . Тогда, учитывая, что
. Тогда, учитывая, что 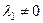 , из условия дополняющей нежесткости (4) получаем
, из условия дополняющей нежесткости (4) получаем
 .
.
Так как, в силу условия неотрицательности (3):  , то
, то 
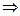
 . При значении
. При значении  функция Лагранжа стремится к
функция Лагранжа стремится к  при
при  . Значит, по следствию из теоремы Вейерштрасса, минимум функции Лагранжа, в силу единственности найденного решения, достигается в точке
. Значит, по следствию из теоремы Вейерштрасса, минимум функции Лагранжа, в силу единственности найденного решения, достигается в точке  . Достаточные условия теоремы Куна-Таккера выполнены, следовательно,
. Достаточные условия теоремы Куна-Таккера выполнены, следовательно,  и
и  .
.
 2017-11-01
2017-11-01 849
849