Решить следующую ЗДП 2

ПРИМЕРЫ ДИНП

 

Задачи распределения ресурсов

Задача № 3.1.1.

Решить следующую ЗДП 1:

где

Рассчитываем таблицы значений функции Беллмана и условно оптимальных управлений (табл. 3.1, 3.2).

Таблица 3.1 Таблица 3.2

j ξ
			5=

j ξ
		0,2
			0,1,2=

 

Пояснения к расчетам приводятся ниже.

Заполнение первых столбцов указанных таблиц осуществляется на основе соотношения:

. Очевидно, что max здесь определяется значением x [1]=[ξ/3]. Поэтому подробные расчеты не приводятся.

Заполнение вторых столбцов осуществляется на основе следующего рекуррентного соотношения: .

Ненулевые значения, очевидно, получаются при :

; ;

; .

Расчет единственного необходимого элемента третьего столбца (для ) осуществляется на основе следующего рекуррентного соотношения: :

.

Расчет всех эквивалентных оптимальных решений (безусловно оптимальных планов) обратным ходом по массиву условно оптимальных управлений с помощью ветвящейся процедуры:

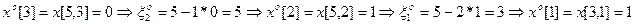
Домашнее задание

Решить следующую ЗДП 1:

 

Решить следующую ЗДП 2

 

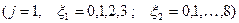Этап 1. Рассчитываем значения функции Беллмана и условно оптимальных управлений , . Результаты оформляем в виде таблиц, представляющих сечения указанных выше трехмерных массивов по значениям (вычисления для =0 опускаем ввиду их тривиальности для рассматриваемой задачи: , ).

При заполнении первых столбцов приведенных таблиц решается достаточно тривиальная оптимизационная задача следующего вида:

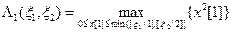
Так как целевая функция монотонно возрастающая, то решение находится на правой границе оптимизационной переменной, т.е. определяется значением . Поэтому подробные расчеты не приводятся. Результаты показаны в первых столбцах табл. 3.3 – 3.8.

 

j

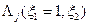Таблица 3.3 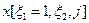Таблица 3.4

j

j

 

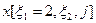Таблица3.5 Таблица 3.6

j

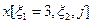Таблица 3.7 Таблица 3.8

j
		11=

j
		2=

 

Приведем лишь расчеты заключительных элементов таблиц, выполняемых на основе следующего рекуррентного соотношения:

.

.

Этап 2. Определение безусловно оптимальных управлений путем обратного хода по массиву условно оптимальных управлений:

.

Оптимальное решение: =11, =(1,2).

Решить следующую ЗДП 3:

Решение (см. раздел 4.1.1.3.в [1]):

Этап 1. Рассчитываем значения функции Беллмана и условно оптимальных управлений , , . Результаты оформляем в виде таблиц, представляющих сечения указанных выше трехмерных массивов по значениям (вычисления для =0 опускаем ввиду их тривиальности для рассматриваемой задачи: , , ).

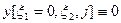При заполнении первых столбцов приведенных таблиц решается достаточно тривиальная оптимизационная задача следующего вида:

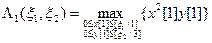
Так как целевая функция монотонно возрастающая, то решение находится на правых границах оптимизационных переменных, т.е. определяется значениями . Поэтому подробные расчеты не приводятся. Результаты расчетов приведены в первых столбцах табл. 3.9 – 3.17.

Приведем лишь расчеты заключительных элементов таблиц, выполняемых на основе следующего рекуррентного соотношения:

.

.

 

 

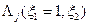Таблица 3.9 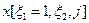Таблица 3.10 Таблица3.11

j

j			j

 

Таблица3.12 Таблица 3.13 Таблица 3.14

j

j			j

 

Таблица 3.15 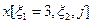Таблица 3.16 Таблица 3.17

j
		39=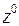

j				j
		0=			2=

 

Этап 2. Определение безусловно оптимальных управлений путем обратного хода по массиву условно оптимальных управлений:

Оптимальное решение: 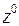=39, =(3,0), .