Ι. Первое приближение.
Принимаем в первом приближении 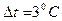 . Тогда температура стенки со стороны греющего пара равняется:
. Тогда температура стенки со стороны греющего пара равняется:
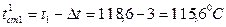 .
.
Тогда по формуле (3.37) получаем:
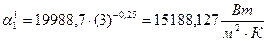 .
.
При этом удельный тепловой поток от пара к стенке равен:
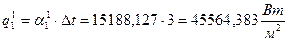 .
.
Сумма термических сопротивлений равна:
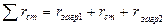 ,
,
где 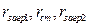 - соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора. По (/1/, табл. XXXI, стр. 531) находим:
- соответственно термические сопротивления загрязнений со стороны греющего пара, стенки и со стороны раствора. По (/1/, табл. XXXI, стр. 531) находим:
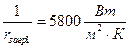 ,
,
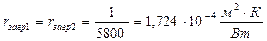 .
.
Для стенки: 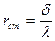 ,
,
где 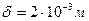 - толщина стенки,
- толщина стенки, 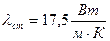 - коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529).
- коэффициент теплопроводности стали (/1/, табл. XXVIII, стр. 529).
 ,
,
 .
.
Поскольку удельный тепловой поток от пара к стенке  равен удельному тепловому потоку через стенку
равен удельному тепловому потоку через стенку 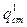 , то можно получить:
, то можно получить:
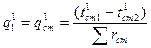 ,
,
при этом 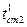 - температура стенки со стороны раствора рассчитывается по формуле (3.38):
- температура стенки со стороны раствора рассчитывается по формуле (3.38):
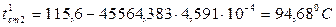 .
.
При температуре 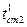 коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
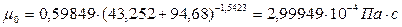 ,
,
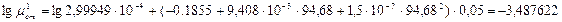
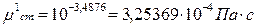 .
.
По формуле (3.46) находим в коэффициент теплоотдачи от раствора к стенке:
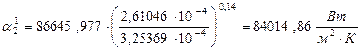 .
.
Тогда удельный тепловой поток от стенки к раствору вычисляется по формуле (3.39):
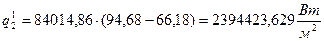 .
.
Расхождение между  и
и 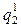 в первом приближении составляет
в первом приближении составляет
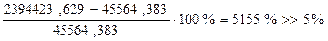 .
.
ΙΙ. Второе приближение.
Принимаем во втором приближении 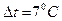 . Тогда температура стенки со стороны греющего пара равняется:
. Тогда температура стенки со стороны греющего пара равняется:
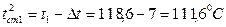 .
.
Тогда по формуле (3.37) получаем:
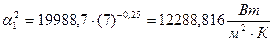 .
.
При этом удельный тепловой поток от пара к стенке равен:
 .
.
Температуру стенки со стороны раствора 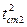 рассчитываем по формуле (3.38):
рассчитываем по формуле (3.38):
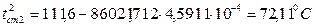 .
.
При температуре 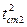 коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
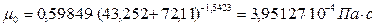 ,
,
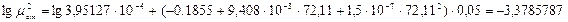
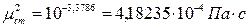 .
.
По формуле (3.46) находим в коэффициент теплоотдачи от раствора к стенке:
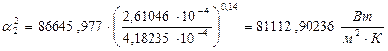 .
.
Тогда удельный тепловой поток от стенки к раствору вычисляется по формуле (3.39):
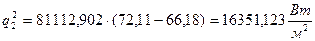 .
.
Расхождение между 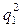 и
и 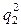 в первом приближении составляет
в первом приближении составляет
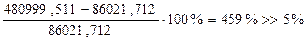 .
.
Составляем таблицу 3.5, в которую заносим результаты первого и второго приближений, а также проверочный расчет.
Таблица 3.5
Результаты приближений
| Приближения и проверочный расчет | Конденсация греющего пара | |||||
| 
| 
| 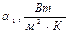
| 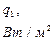
| ||
| I | 118,6 | 115,6 | 3,0 | 15188,13 | 45564,38 | |
| II | 118,6 | 111,6 | 7,0 | 12288,816 | 86021,71 | |
| III | 118,6 | 110,7 | 7,9 | 11922,787 | 94190,015 | |
| Приближения и проверочный расчет | Стенка и ее загрязнения | Нагревание раствора | ||||
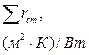
| 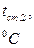
| 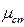 , Па·с , Па·с
| 
| 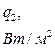
| ||
| I | 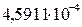
| 94,68 | 3,25·10-4 | 84014,864 | 2394423,629 | |
| II | 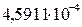
| 72,11 | 4,18·10-4 | 81112,902 | 480999,511 | |
| III | 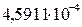
| 67,46 | 8,56·10-4 | 73375,601 | 93920,769 | |
По результатам расчетов первого и второго приближения строим график 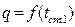 . Полагая, что при малых изменениях температуры, поверхностные плотности
. Полагая, что при малых изменениях температуры, поверхностные плотности 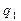 и
и 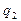 линейно зависят от
линейно зависят от 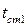 , графически определяем
, графически определяем 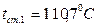 (рис. 3.5, точка В).
(рис. 3.5, точка В).
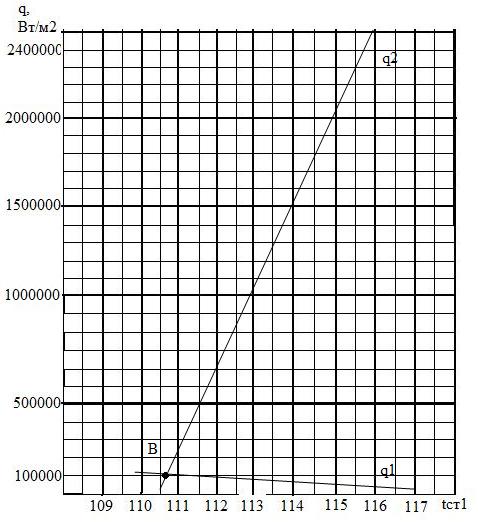
Рис. 3.5 Графическая зависимость 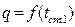
ΙΙΙ. Проверочный расчет
Температура стенки со стороны греющего пара 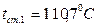 .
.
Δt = t1 – tст1 = 118,6 – 110,7 = 7,9 °С
Тогда по формуле (3.37) получаем:
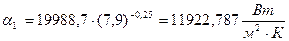 .
.
При этом удельный тепловой поток от пара к стенке равен:
 .
.
Температуру стенки со стороны раствора 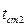 рассчитываем по формуле (3.38):
рассчитываем по формуле (3.38):
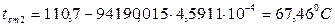 .
.
При температуре 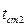 коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
коэффициент теплопроводности, вычисленный по формуле (3.34) равен:
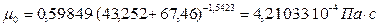 ,
,
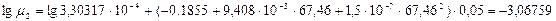
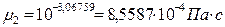 .
.
По формуле (3.46) находим в коэффициент теплоотдачи от раствора к стенке:
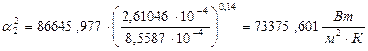 .
.
Тогда удельный тепловой поток от стенки к раствору вычисляется по формуле (3.39):
 .
.
Расхождение между 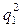 и
и 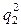 в первом приближении составляет
в первом приближении составляет
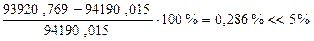 .
.
Коэффициент теплопередачи равен:
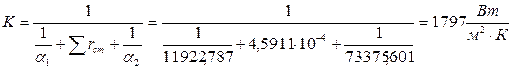 .
.
Поверхность теплообмена:
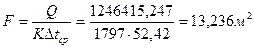
Поверхностная плотность теплового потока:
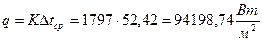 ,
,
Определение температуры внутренней поверхности труб  :
:
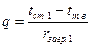 ; (3.40)
; (3.40)
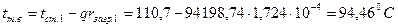 .
.
Определение температуры наружной поверхности труб:
 ; (3.41)
; (3.41)
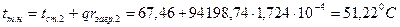 .
.
Средняя температура стенок труб:
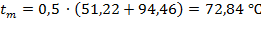 .
.
Средняя разность:
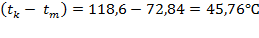 .
.
Величина 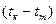 меньше 50 К (/1/, табл.ХХХV, стр. 534), поэтому (/1/, стр. 213) принимаем кожухотрубчатый горизонтальный теплообменник с подвижными трубными решетками типа ТНГ.
меньше 50 К (/1/, табл.ХХХV, стр. 534), поэтому (/1/, стр. 213) принимаем кожухотрубчатый горизонтальный теплообменник с подвижными трубными решетками типа ТНГ.
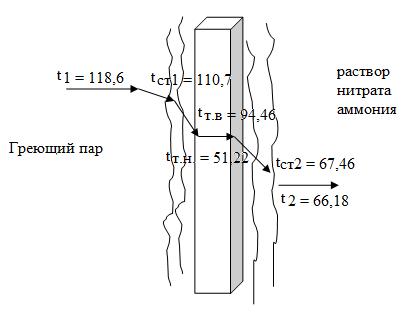
Рис. 3.6 Схема теплопередачи при ламинарном режиме
 2017-11-01
2017-11-01 642
642








