Контрольная работа 1 по математике

Вариант 4

1. Решить систему линейных алгебраических уравнений методом Гаусса

2. Даны координаты вершин пирамиды :

Требуется найти:

1) длину ребра ;

2) угол между ребрами 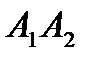и ;

3) угол между ребром и гранью ;

4) площадь грани ;

5) объем пирамиды; 6) уравнения прямой ;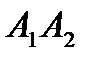

7) уравнение плоскости ;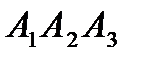

8) уравнения высоты, опущенной из вершины на грань .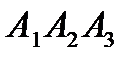

Сделать чертеж.

3. Написать уравнение кривой, модуль разности расстояний от каждой точки которой до точек и равен 4. Сделать чертеж.

4. Дано комплексное число .

Требуется:

1) записать число в алгебраической и тригонометрической формах;

2) найти все корни уравнения .

 

 

5. Найти пределы функций, не пользуясь правилом Лопиталя:

а) ; б) .

6. Найти производные данных функций:

а) ; б) .

7. Найти неопределенные интегралы:

а) б)

8. Вычислить площадь фигуры, ограниченной графиками функций:

 

 

Контрольная работа 1 по математике

Вариант 5

1. Решить систему линейных алгебраических уравнений методом Гаусса

2. Даны координаты вершин пирамиды :

Требуется найти:

1) длину ребра ;

2) угол между ребрами 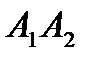и ;

3) угол между ребром и гранью ;

4) площадь грани ;

5) объем пирамиды; 6) уравнения прямой ;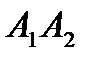

7) уравнение плоскости ;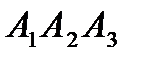

8) уравнения высоты, опущенной из вершины на грань .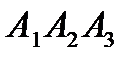

Сделать чертеж.

3.Написать уравнение кривой, каждая точка которой находится на одинаковом расстоянии от точки и от оси . Сделать чертеж.

4. Дано комплексное число .

Требуется:

1) записать число в алгебраической и тригонометрической формах;

2) найти все корни уравнения .

 

5. Найти пределы функций, не пользуясь правилом Лопиталя:

а) ; б) .

6. Найти производные данных функций:

а) ; б) .

7. Найти неопределенные интегралы:

а) б)

8. Найти площадь поверхности, образованной вращением вокруг оси дуги кривой от до .